elliptische kurven - Universität Würzburg

ELLIPTISCHE KURVEN
mit Anwendungen in der Kryptographie
Steffen Reith & Rasa & Jörn Steuding
Universität Würzburg, Wintersemester 2009/10
Topologisch ist eine elliptische Kurve eigentlich nichts anderes als ein ’donut’ oder (mathematisch korrekter) ein Torus, was das Titelbild erklärt. In
dieser Vorlesung beschäftigen wir uns jedoch mehr mit den arithmetischen
und geometrischen Eigenschaften elliptischer Kurven sowie insbesondere deren Anwendungen in der Kryptographie.
Für den Zahlentheoretiker sind rationale Punkte auf elliptischen Kurven
interessant. Hier gibt es Zusammenhänge mit gewissen diophantischen Gleichungen (z.B. der Fermat-Gleichung) oder etwa dem so genannten Kongruenzzahlproblem: Gegeben eine natürliche Zahl n, entscheide man, ob es ein
rechtwinkliges Dreieck mit rationalen Seitenlängen und Flächeninhalt n gibt!
Ein Kryptograph hingegen studiert elliptische Kurven stets über endlichen
Körpern. In den letzten Jahren wurden eine Vielfalt von Ergebnissen, Algorithmen und Implementationstechniken entwickelt, die dazu führen, dass mittelfristig die Kryptographie mit elliptischen Kurven die klassischen Verfahren
in vielen Gebieten ablösen wird, benötigen Kryptosysteme, die auf elliptischen Kurven basieren, doch wesentlich kleinere Schlüssel als die Klassiker.
Tatsächlich kommt die Kryptographie mit elliptischen Kurven heute schon
in Systemen mit wenigen Ressourcen zum Einsatz (eingebettete Systeme),
wie z.B. Steuergeräte im Automobil (bei elektronischen Wegfahrsperren, als
Tuning-Schutz oder in der Car-2-Car Kommunikation).
Die Theorie der elliptischen Kurven hat sich rasant entwickelt. In dieser
Einführung werden wir daher nur die Fundamente der Theorie ergründen.
Unsere Hauptinteressen sind dabei Anwendungen elliptischer Kurven auf zahlentheoretische Fragestellungen und Kryptogrphie. Dies erfordert einen Spagat zwischen Tiefe und Breite. Wir werden nicht alle Theoreme in ihrer vollen
Allgemeinheit beweisen können. Auch werden wir nicht alle notwendigen Hilfsmittel aus anderen mathematischen Disziplinen herleiten.
Die Vorlesung wird von zwei Dozenten gelesen - Steffen Reith (jeweils am
Montag von 10 bis 11:30 Uhr im Raum SE 08), der über die kryptographischen
Aspekte vorträgt, und - Jörn Steuding (jeweils am Freitag von 10 bis 11:30 Uhr
ebenda), der zu den theoretischen Zusammenhängen vorliest. Begleitend gibt
es eine Übung (jeweils montags von 17 bis 18:30 Uhr im SE 36). In der Vorlesung wird eine elementare Herangehensweise vorgenommen, d.h. Kenntnisse
der algebraischen Geometrie und der Funktionen- oder Zahlentheorie werden
nicht benötigt. Alle Algorithmen werden jedoch ohne Voraussetzungen hergeleitet.
Dies ist nur ein Vorlesungsskript und enthält womöglich den ein oder anderen (Druck-)Fehler. Vielen Dank an Peter Dinges und Florian Göpfert für
Fehlerlesen und Korrekturen einer älteren Version. Weitere Verbesserungsvorschläge und Kommentare sind daher herzlich willkommen.
Viel
Spaß!
Inhaltsverzeichnis
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Was sind elliptische Kurven?
Elliptische Kurven über den reellen und den rationalen Zahlen
Die Gruppenstruktur elliptischer Kurven
Reduktion modulo p
Die Assoziativität des Gruppengesetzes
Fermats ’descente infinie’
Der Satz von Mordell
Torsion
Die Vermutung von Birch & Swinnerton-Dyer
Das Kongruenzzahlproblem
Literaturverzeichnis
1
13
18
24
31
35
41
48
56
63
71
II
1. Was sind elliptische Kurven?
1
1. Was sind elliptische Kurven?
Keine Ellipsen! Letztere lassen sich durch Gleichungen der Form
(X/a)2 + (Y /b)2 = 1
mit nichtverschwindenden reellen Zahlen a, b beschreiben. Mit der Parametrisierung x(t) = a cos t, y(t) = b sin t ergibt sich deren Bogenlänge als ein
elliptische Integral (zweiter Art):
Z π/2 p
Z 2π p
2
2
( dx/ dt) + ( dy/ dt) dt = 4
a2 cos2 t + b2 sin2 t dt.
0
0
Im Allgemeinen lässt sich dieses Integral nicht elementar integrieren (eine Ausnahme ist natürlich der Kreis, wenn also a = b gilt). Mit Hilfe von elliptischen
Kurven findet man jedoch für diese elliptischen Integrale eine nicht-elementare
Stammfunktion (was ein Thema der Funktionentheorie ist und deshalb in dieser Vorlesung nicht hergeleitet werden wird).
Tatsächlich sind elliptische Kurven spezielle algebraische Kurven über einem Körper K. Dabei bedeutet das Attribut ’algebraisch’ im Wesentlichen,
dass die Kurve durch eine algebraische Gleichung beschrieben werden kann.
Im Falle elliptischer Kurven handelt es sich dabei um glatte kubische Kurven
(ein Begriff, den wir weiter unten noch präzisieren werden) und die definierende algebraische Gleichung lässt sich meist in die Form
E :
Y 2 = X 3 + aX + b
bringen, wobei a, b irgendwelche festen Koeffizienten aus dem Körper K sind,
von denen wir bis auf weiteres der Einfachheit halber annehmen wollen, dass es
ganze Zahlen sind. Wir bezeichnen mit E(K) die Menge der Punkte (x, y) ∈
K2 , die dieser Gleichung genügen, also Koordinaten im Körper K besitzen,
sowie einem unendlich fernen Punkt, dessen wahre Relevanz sich allerdings
erst später wirklich erschließen wird.
Insbesondere die ganzzahligen bzw. die rationalen Punkte auf einer solchen
Kurve sind von arithmetischem Interesse. Insofern sind elliptische Kurven Spezialfälle so genannter diophantischer Gleichungen, also algebraische Gleichungen mit rationalen Koeffizienten, die auf Lösbarkeit in ganzen oder rationalen
Zahlen untersucht werden. Die Namensgebung ist zu Ehren des griechischen
Mathematikers Diophant, der im dritten Jahrhundert n. Chr. in Alexandrien
lebte. Über sein Leben ist nur sehr wenig bekannt; seine Werke, insbesondere
seine bahnbrechende ’Arithmetica’, waren lange verschollen und wurden erst
im 16. Jahrhundert wieder entdeckt. Ein berühmtes diophantisches Problem
ist die Fermatsche Vermutung, welche Fermat in sein Exemplar der Diophantschen ’Arithmetica’ notierte:
”Es ist unmöglich, einen Kubus in zwei Kuben zu zerlegen,
oder ein Biquadrat in zwei Biquadrate, oder allgemein irgendeine Potenz größer als die zweite in Potenzen gleichen
2
ELLIPTISCHE KURVEN
Abbildung 1. Links: Diophants Buch ’Arithmetica’ in einer Ausgabe
des 17. Jahrhunderts. Rechts: Pierre de Fermat, ∗ 1607/08 Beaumont-deLomagne – † 1665 Castres; französischer Jurist und Mathematiker, der
nicht nur in der Zahlentheorie wichtige Akzente setzte, sondern auch Mitbegründer der analytischen Geometrie und der Differential- und Integralrechnung war.
Grades. Ich habe einen wahrhaft wunderbaren Beweis gefunden, aber dieser Rand ist zu schmal, ihn zu fassen.”∗
In moderner mathematischer Sprache bedeutet dies: Die Gleichung
Xn + Y n = Zn
mit ganzzahligem
n≥3
besitzt nur triviale Lösungen in ganzen Zahlen, d.h. also genau solche Lösungen
x, y, z ∈ Z, die man sofort sieht: xyz = 0. (Wir notieren Unbekannte üblicherweise mit Großbuchstaben und Lösungen mit den entsprechenden Kleinbuchstaben.) Fermats ’Beweis’ ist jedoch nie aufgetaucht; heute geht man davon
aus, dass Fermat keinen stichhaltigen Beweis hatte. Die Fermatsche Vermutung wurde schließlich 1995 von Andrew Wiles gelöst. Sein Beweis basiert auf
einer Brücke zwischen elliptischen Kurven und Modulformen (das sind holomorphe Funktionen der oberen Halbebene, die einer Vielzahl von Funktionalgleichungen genügen, gewissermaßen automorph bzgl. der Gruppe SL2 (Z) sind)
und ist eine Perle der modernen Mathematik. Tatsächlich handelt es sich aber
nur im kubischen Fall bei der Fermat-Gleichung um eine elliptische Kurve im
folgenden Sinne: Mit der Transformation U = X/Z, V = Y /Z schreibt sich die
Fermat-Gleichung um zu
Un + V n = 1
Lateinisch: ”Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem
nominis fas est dividere. Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis
exiguitas non caperet.”
∗
1. Was sind elliptische Kurven?
3
und die Fermatsche Vermutung besteht nun in dem Problem, rationale Lösungen zu finden. Dabei gehen nur triviale ganzzahlige Lösungen verloren. Falls
der Exponent n = 3 ist, handelt es sich um eine glatte kubische und damit
also elliptische Kurve. Vermöge der Transformation
36 + Y
36 − Y
, V =
6X
6X
wird die Gleichung der Fermat-Kurve auf so genannte Weierstraß-Normalform
gebracht:
U=
U3 + V 3 = 1
−→
Y 2 = X 3 − 432.
(Nachrechnen erlaubt!) Mit der Transformation
X=
U −V
12
, Y = 36
U +V
U +V
lässt sich dies auch umkehren, womit also eine birationale Abbildung zwischen
diesen beiden Kurven bzw. Gleichungen gegeben ist; hierbei bedeutet birational, dass die Bijektion zwischen den Kurven rationale Punkte auf rationale
Punkte abbildet (bis auf endlich viele Ausnahmen). Dabei ist natürlich zu
beachten, dass bei Körpern der Charakteristik zwei oder drei hier Probleme
auftreten.
Zur weiteren Illustration unserer bislang nur provisorischen Definition elliptischer Kurven und der Problematik verschiedener Erscheinungsformen kubischer Kurven untersuchen wir ein der Fermat-Kurve zum Exponenten n = 3
verwandtes Beispiel. Zwischen den beiden ebenen kubischen Kurven
U 3 + V 3 = 1729
←→
Y 2 = X 3 − 1 291 438 512
besteht eine ’birationale Äquivalenz’ vermöge der bijektiven Abbildung
U 7→ X :=
20 748
,
U +V
V 7→ Y := 62 244
U −V
.
U +V
Wie man solche birationalen Abbildungen findet, entnimmt man etwa dem
Buch [4] von Knapp. Übrigens wusste bereits Ramanujan, dass die Ausgangsgleichung nur zwei Lösungen in ganzen Zahlen besitzt:
1729 = 13 + 123 = 93 + 103 ,
(was man unschwer mit den Faktorisierungen U 3 +V 3 = (U +V )(U 2 −U V +V 2 )
und 1729 = A · B beweist). Demgegenüber besitzt die transformierte rechte
Gleichung nur endlich viele rationale Lösungen (was insbesondere Ramanujan’s Beobachtung über die Endlichkeit der ganzzahligen Lösungen impliziert).
Warum solche Kurven für Zahlentheoretiker einerseits und für Kryptographen andererseits so interessant sind, wird sich uns recht bald erschließen.
Zunächst wollen wir aber elliptische Kurven im Kontext algebraischer Kurven
betrachten (auch wenn dieser algebraisch-geometrische Standpunkt letztlich
nicht Gegenstand dieser ’elementaren’ Vorlesung sein wird).
4
ELLIPTISCHE KURVEN
Abbildung 2. Links die reelle Kurve X 3 + Y 3 = 1729, rechts die
reelle Kurve Y 2 = X 3 − 1 291 438 512 (beide mit den jeweiligen rationalen
Punkten aus dem Text).
Im Folgenden sei K ein Körper (z.B. der Körper Q der rationalen Zahlen
oder der Körper R reellen Zahlen oder die komplexen Zahlen oder aber auch
ein endlicher Körper) und K ein algebraischer Abschluß (also der Körper der
durch Adjunktion der Wurzeln sämtlicher algebraischen Gleichungen mit Koeffizienten in K entsteht, wie z.B. der Körper der komplexen Zahlen C = R
nach dem Fundamentalsatz der Algebra der algebraische Abschluß von R ist).
Eine ebene algebraische Kurve C über K ist definiert durch eine Gleichung
P (X , Y) = 0,
wobei P ∈ K[X , Y]
irreduzibel über K ist (sich also nur trivial faktorisieren lässt). Der Grad von
C bzw. des Polynoms
X
P (X , Y) =
aij X i Y j
i,j
ist dann definiert durch
deg C = deg P = max{i + j : aij 6= 0}.
Ein Punkt (x, y) ∈ K2 mit P (x, y) = 0 heißt ein K-rationaler Punkt von C und
die Menge aller solchen Punkte notieren wir mit C(K). Hier ein Beispiel: Die
Gleichung
X Y 2 − 6X 2 − 11 = 0
definiert eine ebene Kurve über Q vom Grad drei und etwa ( 21 , 5) ∈ C(Q).
In diesem Zusammenhang sei ein interessantes Problem erwähnt. Auf dem
Internationalen Mathematikerkongress 1900 in Paris stellte Hilbert insgesamt
23 Probleme, welche die Entwicklung der Mathematik im zwanzigsten Jahrhundert wesentlich beeinflußt haben. Das zehnte Hilbertsche Problem lautet:
”Eine diophantische Gleichung mit irgend welchen Unbekannten und mit ganzen rationalen Zahlencoefficienten sei vorgelegt:
man soll ein Verfahren angeben, nach welchem sich mittelst einer endlichen Anzahl von Operationen entscheiden läßt, ob die
Gleichung in ganzen rationalen Zahlen lösbar ist.”
1. Was sind elliptische Kurven?
5
In moderner Sprache ist also nach einem Algorithmus gefragt, mit dessen Hilfe
man in einer endlichen Anzahl von Schritten entscheiden kann, ob ein Polynom
in mehreren Veränderlichen und mit ganzzahligen Koeffizienten, eine ganzzahlige Lösung besitzt. Yuri Matjasevich gab 1970 eine negative Antwort auf das
zehnte Hilbertsche Problem: Es gibt keinen Algorithmus, der entscheidet ob
eine beliebig gegebene diophantische Gleichung in ganzen Zahlen lösbar ist! Erstaunlicherweise ist über den rationalen Zahlen dieselbe Frage noch ungelöst.
Hierzu gibt es ein ’Bonmot’ von Henri Darmon:
“In other words: a number theorist cannot be replaced by a
computer! ”
Für eine Teilklasse von diophantischen Gleichungen, wie etwa die Menge der
elliptische Kurven definierenden Gleichungen, ist jedoch Matyasevichs Antwort unbrauchbar. Für Teilklassen wie etwa polynomielle Gleichungen in zwei
Veränderlichen ist bislang ein Algorithmus nicht ausgeschlossen.
Als Nächstes wollen wir den Begriff algebraischer Kurven etwas präzisieren.
Gegeben ein Polynom P ∈ K[X , Y] vom Grad deg P = d, definieren wir das
zugehörige homogenisierte Polynom vom Grad deg P = d durch
P̃ (X, Y, Z) := Z d P (X/Z, Y /Z);
hierbei wird also X = X/Z und Y = Y /Z gesetzt und jedes Monom durch
Multiplikation von Potenzen von Z auf Gesamtgrad d gebracht. Beispielsweise
gilt
P (X , Y) = Y 2 − X 3 − X − 7
→
P̃ (X, Y, Z) = Y 2 Z − X 3 − XZ 2 − 7Z 3 .
Dann erhält man das Ausgangspolynom P vermöge P (X , Y) = P̃ (X , Y, 1).
Diese Konstruktion ist interessant mit Blick auf die projektive Ebene P2 (K),
welche aus der affinen Ebene K2 durch den Quotienten
P2 (K) = (K3 \ {0})/(K \ {0})
mittels der Äquivalenzrelation
(a, b, c) ∼ (λa, λb, λc)
für λ ∈ K
entsteht. Man beachte, dass nebenbei
P̃ (λa, λb, λc) = λd P̃ (a, b, c)
gilt. Jede Äquivalenzklasse wird mit (a : b : c) notiert und die projektive
Ebene P2 (K) kann entsprechend mit den Geraden durch den Ursprung 0 in
K3 identifiziert werden. Dabei wird die affine Ebene K2 durch Hinzufügen
einiger unendlich ferner Punkte kompaktifiziert und die Einbettung
K2 ֒→ P2 (K2 ),
(a, b) 7→ (a : b : 1)
ist nahezu bijektiv (bis eben auf die unendlich fernen Punkte (a : b : 0), welche
die projektive Gerade P1 (K) bilden). Damit beschreibt P̃ (X, Y, Z) = 0 den
projektiven Abschluss C˜ in P2 (K) der algebraischen Kurve P (X , Y) = 0
6
ELLIPTISCHE KURVEN
Abbildung 3. Zwei Beispiele reeller singulärer kubischer Kurven.
Links die Neilsche Parabel Y 2 = X 3 , welche singulär im Ursprung ist,
rechts die Kurve Y 2 = X 2 (X + 1) mit einem Dopplepunkt im Ursprung.
in der affinen Ebene K2 . Die projektive Kurve C˜ besteht dann aus der affinen
Kurve C und einigen unendlich fernen Punkten; im obigen Beispiel:
˜ Q) = C(Q) ∪ {O}
C(
mit O = (0 : 1 : 0).
Dieser unendlich ferne Punkt O wird sich insbesondere bei elliptischen Kurven
als äußerst wichtig erweisen. Der Vorteil der projektiven Sichtweise ergibt sich
aus dem Satz von Bezout, der besagt, dass zwei projektive Kurven F (X, Y, Z) =
0 und G(X, Y, Z) = 0 vom Grad m bzw. n sich in genau mn Punkten des
P2 (K) schneiden, wobei wir Vielfachheiten zählen (wie etwa im Tangentialfall),
sofern F und G keinen gemeinsamen nicht-trivialen Faktor haben (klar) und K
algebraisch abgeschlossen sei. Jede von diesen Bedingungen ist natürlich und
kann nicht ausgelassen werden. Einen Beweis des Satzes von Bezout findet man
etwa bei Knapp [4]. Bei elliptischen Kurven können wir also beim Schnitt mit
irgendwelchen Geraden stets von drei Schnittpunkten ausgehen! Im Affinen
ist diese Aussage hoffnunglos falsch, wie etwa das Beispiel zweier paralleler
Geraden lehrt. Aber auch bei anderen algebraischen Kurven ist die projektive
Sichtweise von Bedeutung.
Eine affine Kurve C : P (X , Y) = 0 heißt nicht-singulär bzw. glatt (im
Falle perfekter Körper K), wenn für alle Punkte (x, y) auf C der Gradient in
diesem Punkt nicht verschwindet, also nicht alle partiellen Ableitungen gleich
Null sind:
∂P
∂P
oder
6= 0 ;
gradP (x, y) 6= 0 ,
d.h.
∂x
∂y
andernfalls nennen wir (x, y) singulär. Die projektive Kurve C˜ heißt nichtsingulär, wenn alle affinen ’Teile’ nicht-singulären sind, d.h. die Kurven
P̃ (X, Y, 1) = 0 bzw. P̃ (X, 1, Z) = 0 bzw. P̃ (1, Y, Z) = 0
1. Was sind elliptische Kurven?
7
Abbildung 4. Links: Claude Gaspar Bachet de Méziriac, ∗ 9. Oktober 1581, – † 26. Februar 1638 in Bourg-en-Bresse; übersetzte u.a. die
’Arithmetica’ des Diophant in das Lateinische, was die Zahlentheorie aus
der Vergessenheit des Mittelalters führte. Rechts: Euklid, ∗ 325 v. Chr., –
† ca. 265 v. Chr. in Alexandria; bedeutender griechischer Mathematiker,
Verfasser der ’Elemente’ und Begründer der Zahlentheorie.
nicht-singulär sind; man beachte, dass diese affinen Teile zusammen genommen
eine Überdeckung von C˜ liefern. Ist (x, y) nicht-singulär und K = R, so ist C
um den Punkt (x, y) lokal eine glatte Kurve; für K = C hingegen sieht C
lokal wie die komplexe Ebene C aus und definiert eine kompakte Riemannsche
Fläche (auch dies ist ein Thema der Funktionentheorie).
Nun wollen wir ebene algebraische Kurven bzgl. ihrer Grade betrachten.
•
deg P = 1: In diesem Fall ist C eine affine Gerade:
aX + bY + c = 0
mit (a, b) 6= (0, 0).
Für a, b, c ∈ Q besitzt diese lineare Gleichung bekanntlich (mit Hilfe des euklidischen Algorithmus und ein wenig elementarer Zahlentheorie) unendlich viele
rationale Lösungen, d.h. – umformuliert in unsere geometrische Sprache – die
Kurve C enthält unendlich viele rationale Punkte (also solche mit rationalen
Koordinaten).
• deg P = 2: In diesem Fall ist C eine affine Quadrik, ist also nach Hauptachsentransformation von der Gestalt
aX 2 + bY 2 + c = 0.
Wir betrachten zunächst den Spezialfall des Einheitskreises
C : X 2 + Y 2 = 1.
Interessant sind auch hier die rationalen Punkte. Wir beschreiben diese mit
einer geometrischen Methode nach Bachet. Wir schneiden den Einheitskreis
8
ELLIPTISCHE KURVEN
Abbildung 5. Der Einheitskreis geschnitten mit der Sekante durch die
Punkte (−1, 0) und ( 35 , − 54 ) (mit Steigung m = − 21 ); dem zweiten Schnittpunkt entspricht das pythagoräische Tripel (3, 4, 5). Man beachte, dass
die Zuordnung zwischen rationalen Punkten und pythagoräischen Tripeln
nicht bijektiv ist.
mit der Geradenschar
Lm : Y = m(X + 1)
für m ∈ Q.
Jede Gerade Lm schneidet den Kreis in dem Punkt (−1, 0) sowie in einem
weiteren Schnittpunkt, dessen Koordinaten sich leicht berechnen als
1 − m2
2m (x, y) =
,
.
1 + m2 1 + m2
Tatsächlich ist also dieser zweite Schnittpunkt genau dann rational, wenn die
Steigung m der Geraden Lm rational ist. Auf diese Weise erhalten wir nicht
nur viele rationale Punkte auf dem Kreis, sondern sogar sämtliche: Die Sekante
durch (−1, 0) und (x, y) ∈ C ∩ Q2 \ {(−1, 0)} besitzt nämlich eine rationale
Steigung und mittels m = uv für ganzzahlige u, v ergibt sich so
u2 − v 2
2uv (x, y) =
,
∈ C.
u2 + v 2 u2 + v 2
Den Punkt (−1, 0) erhalten wir vermöge m → ∞ (dem Fall der Tangente an
(−1, 0)). Damit ergibt sich der klassische
Satz 1 (Euklid). Die ganzzahligen Lösungen x, y, z der Gleichung
X2 + Y 2 = Z2
heißen pythagoräische Tripel; derer gibt es unendlich viele und alle ergeben
sich durch die Parametrisierung
(x, y, z) = (u2 − v 2 , 2uv, u2 + v 2 )
für
u, v ∈ Z.
1. Was sind elliptische Kurven?
9
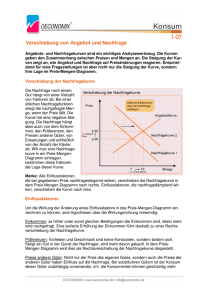
Abbildung 6. Die Ellipse X 2 + 4Y 2 = 4 geschnitten mit der Sekan10
10 12
te durch die Punkte (− 13
, − 12
) und ( 13
, 13 ); Die Parallele durch (2, 0)
13
289
120
10
10 12
schneidet den Kreis im weiteren Punkt ( 169 , − 169
) = (− 13
, − 12
)⊕( 13
, 13 );
13
der Punkt (2, 0) ist das neutrale Element der Gruppe.
Z.B.: 32 + 42 = 52 oder aber 52 + 122 = 132 oder auch
3152 + 49 6122 = 49 6132 .
Ein pythagoräisches Tripel (x, y, z) heißt primitiv, wenn der größte gemeinsame Teiler von x, y, z gleich Eins ist. Wir sehen sofort, dass es auch unendlich viele primitive pythagoräische Tripel gibt! Euklid gab einen arithmetischen Beweis, der im Wesentlichen auf der Faktorisierung Y 2 = Z 2 − X 2 =
(Z − X)(Z + X) unter Berücksichtigung der Parität beruht (siehe etwa [9]).
Bachets Methode funktioniert auf allgemeinen Quadriken – vorausgesetzt es
gibt mindestens einen rationalen Punkt! Auf diese Bedingung kann natürlich
nicht verzichtet werden; die Gleichung X 2 + Y 2 = 3 besitzt keine rationale
Lösungen (wie man leicht bei Betrachtung derselben modulo 9 einsieht).
Als Nächstes zeigen wir, dass eine Quadrik die Struktur einer abelschen
Gruppe besitzt – ein Aspekt, dessen Analogon später von großer Relevanz in
der Theorie der elliptischen Kurven sein wird! Hierbei gehen wir davon aus,
dass die Quadrik bereits auf folgende Hauptachsenform transformiert ist:
d
falls d ≡ 1 mod 4,
2
2
(1)
C : X − ∆Y = 4
mit ∆ =
4d falls d ≡ 2, 3 mod 4,
bei quadratfreiem 1 6= d ∈ Z. Dann wird die Addition zweier Punkte Pj =
(xj , yj ) erklärt durch
P1 ⊕ P2 = (x1 , y1 ) ⊕ (x2 , y2 ) := 21 (x1 x2 + ∆y1 y2 ), 21 (x1 y2 + x2 y1 ) .
Der arithmetische Hintergrund besteht in der Abbildung
√
(x, y) 7→ 12 (x + y d).
Für den Algebraiker ist diese Abbildung ein Homomorphismus von
√ der Gruppe
C(Q) in die Einheitengruppe des quadratischen Zahlkörper Q( d) (genauer:
dessen Ganzheitsrings). Im Falle −d ∈ N ist C eine Ellipse und nur endlich
10
ELLIPTISCHE KURVEN
15
10
5
-5
5
10
15
20
-5
-10
-15
Abbildung 7. Die Hyperbel X 2 − 2Y 2 = 1; die ganzzahligen Punkte
sind fett eingezeichnet, wie etwa (x, y) = (3, 2).
viele ganzzahlige Punkte können überhaupt auf dieser ’beschränkten’ Kurve
liegen; in diesem Falle korrespondieren
√ diese Punkte mit Einheiten in dem
imaginär-quadratischen Zahlkörper Q( d).
Für d ∈ N ist C eine Hyperbel und die beschreibende diophantische Gleichung ist als Pellsche Gleichung bekannt; in diesem Fall existieren stets unendlich viele ganzzahlige Gitterpunkte
auf C, die mit Einheiten in dem reell√
quadratischen Zahlkörper Q( d) korrespondieren. Wir betrachten als Beispiel
einer solchen Gleichung:
(2)
X 2 − 2Y 2 = 1.
Eine solche Hyperbel enthält natürlich viele Punkte, aber liegen auch welche
mit ganzzahligen Koordinaten auf ihr? Auf Grund der Symmetrie ist mit x, y
auch ±x, ±y eine Lösung, wobei jede Kombination von Vorzeichen erlaubt ist,
weil die Unbekannten ja nur quadratisch in der Gleichung auftreten und diese
Quadrate die Vorzeichen ’nicht sehen’. Geometrisch fragen wir nach ganzzahligen Punkten auf einer Hyperbel. Durch Ausprobieren finden wir die Lösung
x = 3 und y = 2 in natürlichen Zahlen und wir erhalten weitere auf folgende
erstaunliche Art und Weise: Zunächst quadrieren wir unsere Lösung
√
√
√
(x + y 2)2 = (3 + 2 2)2 = 17 + 12 2,
dann ist x = 17 und y = 12 eine neue Lösung:
172 − 2 · 122 = 289 − 2 · 144 = 1.
1. Was sind elliptische Kurven?
11
Ferner erhalten wir durch weiteres Potenzieren
√
√
(3 + 2 2)3 = 99 + 70 2
und wiederum ist x = 99 und y = 70 eine Lösung. Mittels
X 2 − 2Y 2 = 1
⇐⇒
(2X )2 − 8Y 2 = 4
transformiert sich Gleichung (2) in die Gestalt (1) und es korrespondieren die
rationalen Punkte (3, 2) ↔ (6, 2) und (6, 2) ⊕ (6, 2) = (34, 12) ↔ (17, 12) =
(3, 2) ⊕ (3, 2). All diese√Lösungen besitzen eine interessante Eigenschaft, sie
approximieren nämlich 2 besser und besser:
√
99
3
17
= 1, 5,
= 1, 416,
= 1, 41428571 . . . , −→ 2 = 1, 41421356 . . .
2
12
70
Übrigens ist das Längenverhältnis bei Din A 4
Länge
29, 7cm
99
=
= ;
Breite
21cm
70
√
warum diese Approximation an 2 eine so gute Wahl für unser Papierformat
ist, erfährt man in [9].
• deg P ≥ 3: Diese Klasse von Kurven umfasst die elliptischen Kurven (für
die zusätzlich noch einige Regularitätsbedingungen erfüllt sein müssen). Ist
d = deg P der Grad des Polynoms P und r die Anzahl der Doppelpunkte, so
heißt
g = 12 (d − 1)(d − 2) − r
das Geschlecht der Kurve C; diese Größe ist eine nicht-negative ganze Zahl
und eine wichtige topologische Invariante der Kurve. Elliptische Kurven
sind nicht-singuläre Kurven vom Geschlecht eins, welche mindestens einen
rationalen Punkt enthalten. Komplexe elliptische Kurven sind kompakte Riemannsche Flächen vom Geschlecht eins. Topologisch sind diese homöomorph
zu einem Torus C/Λ, wobei Λ ein Gitter in der komplexen Zahlenebene C ist.
Verschiedene Gitter führen u.U. zu unterschiedlichen elliptischen Kurven mit
unterschiedlichen analytischen Eigenschaften, jedoch sind alle solche topologisch identisch: Dem einen ’Loch’ eines Torus entsprechend ist das Geschlecht
– also die Anzahl der ’Löcher’ der Riemannschen Fläche – gleich eins.
Ein Beispiel einer kubischen Kurve, die keine elliptische Kurve ist, weil sie
keinen rationalen Punkt besitzt, ist beschrieben durch die Gleichung
U 3 + pV 3 + p2 = 0
mit einer Primzahl p.
Gleichungen wie etwa Y 2 = X(X 2 − 1)(X 2 − 2) führen auf so genannte hyperelliptische Kurven. In einem komplexen Modell besitzt diese kompakte
Riemannsche Fläche zu dieser Gleichung zwei Löcher, besitzt also Geschlecht
zwei. Die Kleinsche Quartik, gegeben durch die Gleichung X 3 Y +Y 3 Z+Z 3 X =
0, ist ein Beispiel einer kompakten Riemannschen Fläche vom Geschlecht drei.
12
ELLIPTISCHE KURVEN
Abbildung 8. Zwei Beispiele nicht elliptischer Kurven. Links ein reelles Bild der Kurve Y 2 = X(X 2 −1)(X 2 −2) vom Geschlecht zwei, rechts die
Kleinsche Quartik vom Geschlecht drei, wie man an den ’Löchern’ abzählen
kann.
Mordell vermutete, dass jede über Q definierte Kurve von einem Geschlecht
echt größer eins nur höchstens endlich viele rationale Punkte enthalten kann.
Dies steht im Gegensatz zu Kurven vom Geschlecht null, also Kegelschnitte
wie z.B. ein Kreis, bzw. elliptische Kurven, die allesamt Geschlecht eins haben
und u.U. unendlich viele rationale Punkte besitzen. Mordells Vermutung wurde 1983 von Gerd Faltings mit Methoden der algebraischen Geometrie bewiesen, der dafür mit der renommierten Fields-Medaille auf dem Internationalen
Kongress für Mathematik 1986 in Berkeley ausgezeichnet wurde:
Satz von Faltings. Eine nicht-singuläre Kurve vom Geschlecht g ≥ 2 besitzt höchstens endlich viele rationale Punkte. (Die Aussage gilt sogar für Krationale Punkte, wobei K ein beliebiger Zahlkörper ist.)
Rationale Lösungen von Gleichungen in zwei Variablen entsprechen ganzzahligen Lösungen assoziierter Gleichungen in drei Variablen; die glatte FermatKurve
U n + V n − 1 = 0,
besitzt Geschlecht 12 (n − 1)(n − 2). Für n = 2 ist das Geschlecht also null und
es gibt mit den pythagoräischen Tripeln tatsächlich unendlich viele Lösungen.
Ist n = 3, so ist das Geschlecht eins und in diesem Fall haben wir es mit einer
elliptischen Kurve zu tun (s.o.); hier bewies bereits Euler die nicht-triviale
Unlösbarkeit bzw. Gauß (einige Ungenauigkeiten bei Euler ausräumend), womit in der nachfolgenden Tabelle das ’ ?’ durch ’endlich viele triviale Lösungen’
ersetzt werden kann. Für n ≥ 4 ist das Geschlecht größer als zwei und Faltings’
Beweis der Mordell-Vermutung zeigt, dass es also zu jedem festen Exponenten
n ebenso nur höchstens endlich viele nicht-triviale Lösungen in ganzen Zahlen
2. Elliptische Kurven über R und Q
13
gibt.
n = 2 g = 0 pythagoräische Tripel
n=3 g=1
?
n≥4 g≥2
<∞
Im allgemeinen Fall einer elliptischen Kurve hingegen können unendlich viele
rationale Punkte existieren, deshalb also das Fragezeichen ’ ?’ in obiger Tabelle, so dass also Geschlecht g = 1 der Grenzfall zwischen der ’einfachen’ Theorie der Kegelschnitte (mit i.A. unendlich vielen rationalen Punkten) und der
’schwierigen’ Theorie höhergeschlechtlicher Kurven mit nur höchstens endlich
vielen rationalen Punkten ist. Dies macht elliptische Kurven in arithmetischer
Hinsicht so interessant!
2. Elliptische Kurven über den reellen und den rationalen Zahlen
Wir starten mit einer klassischen Aufgabe aus Diophants ’Arithmetica’
(Problem 24 in Buch N): Teile eine gegebene Zahl in zwei Zahlen, so dass
deren Produkt gleich einem Kubus minus einer Seite ist. In moderner Sprache
bedeutet dies, zu einer gegebenen rationalen Zahl a weitere rationale Zahlen
x und y zu finden, so dass
y(a − y) = x3 − x
gilt. Wir skizzieren Diophants Lösung am Beispiel a = 6. Die ’triviale’ Lösung
(x, y) = (−1, 0) liegt auf der Geraden
X = λY − 1
mit
λ=3
und Substitution in der obigen kubischen Gleichung führt auf
y(6 − y) = (λy − 1)3 − (λy − 1) = y(27y 2 − 27y + 6)
bzw. nach Kürzen des Faktors y und Lösen der resultierenden quadratischen
26
, x = 17
Gleichung auf y = 27
9 . Ausgehend von dem offensichtlichen rationalen
Abbildung 9. Diophant konstruiert den nicht-trivialen rationalen
Punkt ( 17
, 26 ) durch Schnitt der Tangente X = 3Y − 1 an den trivia9 27
len Punkt (−1, 0) auf der elliptischen Kurve Y (6 − Y ) = X 3 − X.
14
ELLIPTISCHE KURVEN
Punkt (−1, 0) haben wir so einen alles andere als offensichtlichen rationalen
Punkt gefunden! Bei allgemeinem a kommt man durch entsprechende Variation von λ ganz ähnlich zum Ziel kommen. Vermöge der Transformation
X = −X
und
Y =Y −3
ergibt sich aus Diophants Gleichung Y (6 − Y ) = X 3 − X eine elliptische
Kurvengleichung in ’Weierstraßscher Normalform’ (s.u.):
Y 2 = X 3 − X + 9.
Diophants Aufgabe ist eines der ersten Auftreten elliptischer Kurven in der
Geschichte der Mathematik; die spezielle Theorie elliptischer Kurven (bei der
insbesondere die Geometrie der zu Grunde liegenden Kurve eine wichtige Rolle
spielt) geht nach ersten Anfängen bei Bachet und Fermat im 17. Jahrhundert
auf die Arbeiten von Poincaré und Mordell zu Beginn des zwanzigsten Jahrhunderts zurück.
Über dem Körper der reellen Zahlen lassen sich elliptische Kurven sehr
schön als ebene Kurven in der euklidischen Ebene visualisieren. Dabei treten im Wesentlichen zwei Typen auf. Im Folgenden wollen wir stets davon
ausgehen, dass unsere elliptische Kurve in Weierstraßscher Normalform
vorliegt, d.h.
E : Y 2 = X 3 + aX + b
mit a, b ∈ Q,
wobei für die Diskriminante
∆ := −(4a3 + 27b2 ) 6= 0
gelte, also das Polynom X 7→ P (X) = X 3 +aX+b drei verschiedene Nullstellen
besitze, die elliptische Kurve also glatt sei. Entsprechend besitzt P also eine
oder drei reelle Nullstellen und die elliptische Kurve zerfällt über dem Körper
R demzufolge in eine bzw. zwei Zusammenhangskomponenten, je nachdem ob
die Diskriminante positiv oder negativ ist.
Abbildung 10. Daumenkino: Links die elliptische Kurve Y 2 = X(X −
1)(X + 1) mit positiver Diskriminante ∆ = 4, in der Mitte die singuläre
kubische Kurve Y 2 = X(X − 21 )2 mit ∆ = 0 und rechts die elliptische
Kurve Y 2 = X(X − 1)(X + 1) + 3 mit negativer Diskriminante ∆ = −239.
2. Elliptische Kurven über R und Q
15
Um dies einzusehen, nun ein
Exkurs über kubische Gleichungen in einer Veränderlichen. Diese liegen stets in
folgender Form vor:
X 3 + AX 2 + BX + C = 0
mit A, B, C ∈ R,
bzw. gegebenenfalls nach Anwendung einer Tschirnhaus-Transformation X 7→
X = X + A3 in der Gestalt
(3)
X 3 + aX + b = 0
mit a, b ∈ R[A, B, C].
(Die Beschränkung auf reelle Koeffizienten lässt sich ohne weiteres aufheben,
ist aber in unserem Kontext völlig ausreichend.) Wir dürfen also annehmen,
dass kein quadratischer Term in der kubischen Gleichung auftritt. Mehr Freiheit ergibt sich zunächst vermöge des Ansatzes X = u + v, womit sich (3)
übersetzt in
u3 + 3u2 v + 3uv 2 + v 3 + a(u + v) + b = 0
bzw.
u3 + v 3 = −b
und
3uv = −a (bzw. u3 v 3 = −( a3 )3 ).
Wir setzen nun entsprechend U + V = −b und U V = −( a3 )3 und lösen mit
Vietas Wurzelsatz (Z − U )(Z − V ) = 0 bzw.
Z 2 + bZ − ( a3 )3 = 0
durch z = u3 , v 3 . Damit ergibt sich nun die so genannte Formel von Cardano
(auch ’Cardanische Formel’)
r
q
3
x = u1 + v1
mit u1 , v1 = − 2b ± ( 2b )2 + ( a3 )3
als Lösung von (3). Hierbei ist u1 eine der drei komplexen Wurzeln und v1 ist
durch u1 v1 = − a3 festgelegt; weitere Lösungen von (3) ergeben sich durch x =
ζu1 + ζ 2 v1 , ζ 2 u1 + ζv1 , wobei ζ = exp( 2πi
3 ) eine primitive dritte Einheitswurzel
ist. Der Fall nicht-reeller Lösungen (’casus irreduzibilis’) tritt genau dann auf,
wenn
⇐⇒
∆<0
( 2b )2 + ( a3 )3 > 0
(da nämlich −22 33 ∆ = ( 2b )2 +( a3 )3 ) und der Fall ∆ = 0 beschreibt die Existenz
einer mehrfachen reellen Nullstelle.
Wir erinnern, dass die Diskriminante eines Polynoms das Quadrat der Differenzen der Wurzeln des Polynoms ist. Dabei besitzt ein Polynom n-ten Grades
nach dem Fundamentalsatz der Algebra genau n Nullstellen in C; die Diskriminante eines über R definierten Polynoms ist dabei (auf Grund der Symmetrien) stets reellwertig! Die spezielle Form elliptischer Kurven ergibt sich nun
aus der Lösbarkeit kubischer Gleichungen und der Lage der Lösungen bei stetig variierendem Y in der Weierstraßschen Normalform. Besitzen diese reelle
Nullstellen, so treten entweder eine oder drei reelle Nullstellen auf; komplexe
Nullstellen treten nur als Paare komplex konjugierter Zahlen auf.
16
ELLIPTISCHE KURVEN
Abbildung 11. Der Erste, der kubische Gleichungen zu lösen vermochte, war wohl Scipinio del Ferro anfangs des 16. Jahrhunderts (ohne
Bild). Dieser gab auf dem Totenbett sein Wissen an seine Schüler weiter.
Der ’Stotterer’ Nicolo Tartaglia, ∗1499 oder 1500 in Brescia, - †1557 in
Venedig, trat in öffentlichen Wettstreiten mit seinen Lösungen an. Rechts
Girolamo Cardano, ∗1501 in Pavia, - †1576 in Rom, der Tartaglias Formeln
ohne dessen Wissen und ohne dessen Namensnennung in seinem Lehrbuch
’Ars magna sive de Regulis Algebraicis’ 1545 veröffentlichte.
Jetzt wollen wir elliptische Kurven über Q studieren. Da die rationalen
Zahlen eine sehr dünne Teilmenge der reellen Zahlen bilden, ist zunächst nicht
klar, wie reichhaltig E(Q) ⊂ E(R) ist. Wir erinnern uns an die Lösung des
Problems des Diophant zu Beginn dieses Paragraphen. Diophant konstruierte einen rationalen Punkt auf der elliptischen Kurve durch Schnitt mit einer
’rationalen Geraden’. Diese Tangente an den Punkt (−1, 0) schneidet die kubische Kurve in einem dritten Punkt; man beachte dabei, dass der Berührpunkt
(−1, 0) die Vielfachheit zwei besitzt (weil der Berührpunkt der Tangente doppelt zu zählen ist).
Ganz ähnlich verfährt Bachet mehr als ein Jahrtausend später im Fall der
Kurve
E :
Y 2 = X 3 + c,
wobei c eine fest gewählte rationale Zahl ist. Speziell für c = −2 liefert die
implizite Differentiation
2y
dy
= 3x2
dx
dy
3x2
=
dx
2y
bzw.
die Tangentengleichung
L :
Y =
2y 2 − 3x3
3x2
X+
,
2y
2y
also für den Punkt (x, y) = (3, 5) ∈ E(Q) die Geradengleichung
L :
Y =
27
10 X
−
31
10 .
2. Elliptische Kurven über R und Q
17
Durch Schnitt mit der elliptischen Kurve ergibt sich eine kubische Gleichung
in X:
3x2
2y 2 − 3x3 2
= X 3 + c;
X+
2y
2y
diese besitzt drei Nullstellen, nämlich x mit Vielfachheit zwei und eine einfache
dritte Nullstelle ξ, die damit also der Bedingung
3x2 2
= 2x + ξ
2y
genügt (vermöge eines Koeffizientenvergleichs bei X 2 ). Im Spezialfall (x, y) =
(3, 5) ergibt sich so die kubische Gleichung
2
31
27
X
−
= X3 − 2
10
10
27 2
und ξ = ( 10
) −2·3=
129
100 .
Ganz allgemein erhalten wir so
Satz 2 (Bachet). Mit (x, y) ist auch
x4 − 8cx −x6 − 20cx3 + 8c2 ,
4y 2
8y 3
ein Punkt auf E : Y 2 = X 3 + c; besitzt (x, y) ∈ E rationale Koordinaten, so
auch der durch Schnitt mit der Tangenten an (x, y) konstruierte Punkt.
Weil wir ausschließlich rationale Operationen angewandt haben, vererbt sich
die Rationalität bei der Bachetschen Tangentenmethode! In unserem Beispiel
ergibt sich so sukzessive
129 383 2 340 922 881 113 259 286 337 279
→
,
,
.
(x, y) = (3, 5) →
100 1000
76602
76603
Tatsächlich entstehen so für c 6= 1, −432 unendlich viele rationale Punkte!
(Der Beweis ist aber nicht ganz einfach, denn a priori ist nicht klar, dass sich
irgendwann die so konstruierten Punkte nicht wiederholen.)
Diophants Argument bzw. Bachets Methode des Schnittes rationaler Geraden mit algebraischen Kurven führten u.a. zu besagtem geometrischen Beweis
des Euklidischen Satzes 1 über die pythaogräischen Tripel. Insbesondere lässt
sich diese Idee auf allgemeine elliptische Kurven verallgemeinern; ganz wichtig
dabei ist die Existenz eines rationalen Punktes: Ohne einen solchen können gar
keine Tangenten oder Sekanten gebildet werden. Deshalb fordern wir also stets
E(Q) 6= ∅. Auch versagt Bachets Methode im Falle der Kurve, die durch die
Gleichung Y 2 = X 3 + X gegeben ist, wenn wir als Startpunkt (0, 0) wählen. In
diesem Fall existiert nämlich kein dritter Schnittpunkt der Tangente mit der
elliptischen Kurve im Endlichen, allerdings kann man sich durch Hinzufügen
eines unendlich fernen Punktes behelfen.
Uns interessiert hier aber der allgemeine Fall. Beispielsweise liegen die
Punkte P = (−2, 3) und Q = (2, 5) beide sowohl auf der elliptischen Kurve
E : Y 2 = X 3 + 17
18
ELLIPTISCHE KURVEN
als auch auf der Geraden
L :
Y = 12 X + 4;
die Gerade L kann also als Sekante durch die Punkte P und Q betrachtet werden. Für den dritten Schnittpunkt (x, y) besteht dann die kubische Gleichung
( 21 X + 4)2 = X 3 + 17
X 3 − 14 X 2 − 4X + 1 = 0;
⇐⇒
natürlich erfüllen auch die x-Koordinaten von P und Q diese Gleichung. Umformen und Berücksichtigung dieser bereits bekannten Lösungen liefert
X 3 − 41 X 2 − 4X + 1 = 0 = (X − 2)(X + 2)(X − 41 ),
also die x-Koordinate des dritten Schnittpunkts x = 14 . Einsetzen in der Sekantengleichung liefert y = 41 · 12 + 4 = 33
8 . Damit haben wir also den rationalen
Punkt
(x, y) = ( 14 , 33
8 )∈E∩L
gefunden. Durch Spiegeln ergibt sich auf Grund der elliptischen Kurven in
Weierstrass-Form inhärenten Symmetrie auch noch der gespiegelte rationale
Punkt ( 41 , − 33
8 ) ∈ E ∩ L. Bildet man neue Sekanten, entsteht so u.a. der Punkt
1097
,
−
).
Wir haben damit eine Konstruktionsmethode vieler rationaler
( 106
9
27
Punkte auf elliptischen Kurven gefunden. Tatsächlich entstehen auf diese Art
und Weise sämtliche rationalen Punkte! (Aber auch dieser Beweis ist nicht
leicht.)
3. Die Gruppenstruktur elliptischer Kurven
Wir gehen wieder von einer elliptischen Kurve in Normalform
E :
Y 2 = X 3 + aX + b
mit a, b ∈ Q
aus (insbesondere ist also die Diskriminante ∆ 6= 0 und die Kurve ist glatt).
Ferner seien P = (x1 , y1 ) und Q = (x2 , y2 ) Punkte auf E, wobei wir zunächst
x1 6= x2 annehmen wollen. Dann ist die Sekante durch P und Q gegeben durch
die Gerade
y2 − y1
(X − x1 ) + y1 .
L :
Y =
x2 − x1
Man macht sich dann leicht klar, dass die Sekante L neben P und Q einen
weiteren Schnittpunkt mit der elliptischen Kurve E hat (dank des Satzes von
Bezout: eine elliptische Kurve ist eine kubische Kurve, besitzt also im projektiven Raum drei Schnittpunkte mit jeder Geraden). Mit ein wenig Rechnerei
ergibt sich dieser dritter Schnittpunkt als
P ∗ Q = (x3 , y3 )
mit
(4)
1 2
x3 = ( xy22 −y
−x1 ) − x2 − x1 ,
y3 =
y2 −y1
x2 −x1 (x3
− x1 ) + y 1 .
Das Bemerkenswerte ist, dass mit den Koordinaten von P und Q auch die
Koordinaten des dritten Schnittpunktes P ∗ Q rational sind. Denn durch Anwenden der Grundrechenarten verlässt man nicht die Menge der rationalen
3. Die Gruppenstruktur
19
Zahlen – Q ist ein Körper! Ein ähnliches Phänomen ergibt sich auch im Falle
P = Q. In diesem Fall wird die Sekante zur Tangente und es gilt x1 = x2 . Sei
zuerst y1 = y2 6= 0, so errechnet sich die Tangente als
L :
Y =
3x21 + a
(X − x1 ) + y1 ;
2y1
(bzw. analytisch vermöge Bilden des Grenzwertes x2 → x1 in (4)). Der Schnittpunkt mit der elliptischen Kurve ist dann
x3 = (
3x21 +a 2
2y1 )
− 2x1 ,
y3 =
3x21 +a
2y1 (x3
− x1 ) + y 1
(allgemeiner als Bachets Verdopplungsformel aus Satz 2). Im letzten zu diskutierenden Fall ist x1 = x2 und y1 = y2 = 0 und es gibt keinen dritten Schnittpunkt im Endlichen und wir interpretieren deshalb den unendlich fernen Punkt
O = (∞, ∞) als dritten Schnittpunkt (bzw. projektiv O = (0 : 1 : 0)).
In all diesen Fällen ist mit P, Q ∈ E(Q) auch P ∗Q ∈ E(Q), da offensichtlich
die Koordinaten x3 , y3 rationale Funktionen der Koordinaten x1 , y1 von P und
x2 , y2 von Q sowie den Koeffizienten von E sind. Ähnlich verhält es sich, wenn
wir ein anderes Zahlenuniversum als die rationalen Zahlen zugrunde legen,
sofern dieses nur die Struktur eines Körpers besitzt, und die E definierende
Gleichung bzw. die Koordinatenformeln für P ∗Q über K sinnvoll bestehen; im
Falle endlicher Körper K ist Charakteristik zwei problematisch im Hinblick auf
die Verdopplungsformel. Mit Hilfe dieser geometrischen Konstruktion definier-
Abbildung 12. Die verschiedenen Konfiguratione von Schnittpunkten
einer elliptische Kurve mit Geraden.
te Poincaré eine Addition von Punkten auf einer elliptischen Kurve wie folgt:
Zu den Punkten P und Q, wie oben, liegt auch der Punkt P ∗ Q = (x3 , y3 )
auf der elliptischen Kurve. Spiegelt man letzteren an der x-Achse, so entsteht
ein weiterer Punkt auf der elliptischen Kurve; dieser definiere die Summe der
Punkte P und Q, also
P ⊕ Q = (x3 , −y3 ).
Diese Addition ist vollkommen verschieden von der üblichen Addition rationaler oder reeller Zahlen, jedoch respektiert sie die uns so wichtigen Rechengesetze wie Kommutativität (also P ⊕ Q = Q ⊕ P ), Distributivität und Assoziativität (wenngleich der Nachweis der letzten Eigenschaft nicht ganz so einfach
20
ELLIPTISCHE KURVEN
ist, es sei den man argumentiert mit fortgeschrittenen Methoden der Funktionentheorie oder der algebraischen Geometrie). Dabei fungiert der unendlich
ferne Punkt O als neutrales Element (analog zur Null bei der herkömmlichen
Addition), denn es ist P ⊕ O = P für jeden Punkt P auf E. Auch können wir
additiv inverse Elemente erklären: Gilt P ⊕ Q = O, so schreiben wir Q = −P ,
und man verifiziert leicht, dass −P = (x1 , −y1 ) für P = (x1 , y1 ) gilt; insbesondere besitzt also jeder Punkt ein additiv Inverses. Hier wird die wichtige Rolle
des unendlich fernen Punktes O deutlich, spielt er doch die Rolle des neutralen Elementes und ist somit für die Gruppenstruktur der elliptischen Kurve
hinzuzufügen. Tatsächlich kann man jedoch einen beliebigen rationalen Punkt
der Kurve als neutrales Element zu einem geeignet definierten Gruppengesetz
erklären (was sich am besten durch eine projektive Diskussion erklären lässt).
Mehr noch: die rationalen Operationen, mit denen sich die Koordinaten des
durch die Addition erklärten Punktes berechnen, führen für einen beliebigen
Körper nicht aus diesem hinaus. Es gilt also
Satz 3 (Poincaré, 1901). Sei K ein beliebiger Körper, dann ist eine über K
definierte elliptische Kurve
E(K) = {(x, y) ∈ K2 : y 2 = x3 + ax + b} ∪ {O}
zusammen mit der Addition ′ ⊕′ eine abelsche Gruppe mit O als neutralem
Element.
Wir haben den Beweis nahezu vollständig erbracht, lediglich die Assoziativität
verbleibt zu zeigen, was wir in §5 ausführen werden.
Elliptische Kurven können sehr wenige rationale Punkte besitzen. So liegen
auf der Kurve Y 2 = X 3 −X nur die Punkte (0, 0) und (±1, 0) zuzüglich O (wie
wir in §6, Satz 7 zeigen werden). Andere Kurven wie etwa Y 2 = X 3 −2 hingegen
besitzen unendlich viele rationale Punkte. Insofern können wir es also mit
recht unterschiedlichen Gruppen bei elliptischen Kurven zu tun haben. Was
lässt sich allgemein über elliptische Kurven über Q sagen? Genauer: Inwieweit
besitzen die Gruppen E(Q) eine ähnliche Struktur? Licht ins Dunkle brachte
schließlich Louis Mordell. Er bewies eine Vermutung von Poincaré, als er 1922
zeigte, dass es stets endlich viele Punkte gibt, aus denen sich jeder rationale
Punkt durch endlich viele Schnitte von Sekanten und Tangenten konstruieren
lässt. Etwas mathematischer:
Satz 4 (Mordell, 1922). Die Gruppe der rationalen Punkte einer über Q
definierten elliptischen Kurve ist endlich erzeugt, d.h.
E(Q) ≃ Zr × T,
wobei r = rg(E) der Rang von E(Q) und T = Etors (Q) die Torsionsgruppe
aller Elemente endlicher Ordnung ist.
Eine elliptische Kurve E(Q) ist also eine endlich erzeugte abelsche Gruppe.
Die Torsionsgruppe T ist die Menge aller Punkte endlicher Ordnung, also
3. Die Gruppenstruktur
21
Abbildung 13. Links: Henri Poincaré, ∗ 1854 - † 1912. Ein weiterer französischer Mathematiker, der durch seine bahnbrechenden Arbeiten
zum Dreikörperproblem berühmt geworden ist. Die Poincarésche Vermutung über die Topologie von dreidimensionalen Flächen ist eines der sieben
Millenniumsprobleme und wurde vor wenigen Jahren durch Grigori Perelman bewiesen. Rechts: Louis Mordell, ∗ 1888 - † 1972. Bedeutender amerikanischer Zahlentheoretiker litauischer Abstammung, der u.a. die Lösbarkeit polynomieller Gleichungen in ganzen bzw. rationalen Zahlen studierte.
die Menge all der Punkte P , die sich durch fortgesetzte Addition ihrer selbst
letztlich zum neutralen Element O addieren lassen. Solche Punkte sind selten,
denn die Torsionsgruppe ist stets endlich (was sich sofort aus dem Struktursatz für endlich erzeugte abelsche Gruppen ergibt); allerdings liefert dieses
Argument keinerlei Aussage über die Größe von T , noch über die Lage der
Torsionspunkte. Ferner kann man von solchen Punkten P nur endlich viele
weitere Punkte erreichen. Die Größe einer elliptischen Kurve E wird durch
ihren Rang r = rg(E) bestimmt, denn alle Elemente in Zr bis auf das neutrale Element haben unendliche Ordnung, d.h. fortgesetzte Addition ihrer selbst
führt niemals auf das neutrale Element. Also besitzt nach Mordell eine elliptische Kurve E(Q) genau dann unendlich viele rationale Punkte, wenn ihr Rang
rg(E) positiv ist:
♯E(Q) = ∞ ⇐⇒ r(E) > 0.
Der Rang steht für die Anzahl der Punkte, aus denen sich mittels Bachets
Sekanten-Tangenten-Methode jeder rationale Punkt in endlich vielen Schnitten
erreichen lässt. Beispielsweise gilt für die elliptische Kurve zur Gleichung Y 2 =
X3 − 4
E(Q) ≃ Z1 ,
wobei etwa der Punkt (2, 2) alle rationalen Punkte erzeugt. Die Aussage des
Mordellschen Satzes ist falsch für singuläre Kurven wie etwa der singulären
Neilschen Parabel Y 2 = X 3 mit einer Spitze in (0, 0). Wie kann man aber im
Fall einer elliptischen Kurve entscheiden, ob ihr Rang positiv ist oder nicht?
22
ELLIPTISCHE KURVEN
Tatsächlich gibt die Vermutung von Birch & Swinnerton-Dyer hierfür ein Kriterium. (In §9 dazu mehr!) Ein weiteres offenes Problem in diesem Zusammenhang ist die
Rang-Vermutung: lim supE rg(E) = ∞.
Der aktuelle Weltrekord stammt von Elkies aus dem Jahre 2006; wir sollten
nicht darauf verzichten, die definierende Gleichung der Kurve mit ihren etwas
länglichen Koeffizienten niederzuschreiben:
Y 2 + XY + Y
= X3 − X2
−20 067 762 415 575 526 585 033 208 209 338 542 750 930 230 312 178 956 502 X
+34 481 611 795 030 556 467 032 985 690 390 720 374 855 944 359 319 180 361
266 008 296 291 939 448 732 243 429.
Auf der Internetseite http://web.math.hr/∼duje/tors/z1.html findet man 28
’unabhängige’ Punkte unendlicher Ordnung, was rg(E) ≥ 28 aufzeigt (tatsächlich
besteht sogar die Möglichkeit, dass der Rang dieser Kurve noch größer ist).
Hier ist noch ein weiter Weg bis unendlich zu gehen...
4
2
-2
-1
1
2
3
-2
-4
Abbildung 14. Addition (−1, 0) ⊕ (0, 1) = (2, −3) auf der elliptischen
Kurve Y 2 = X 3 + 1. Insgesamt existieren sechs rationale Punkte, welche
sich alle recht schnell mit der Tangenten-Sekanten-Methode aus obigen drei
Punkten ergeben.
Wir geben ein paar Beispiele (hier ohne Beweis):
(i) E : Y 2 = X 3 + 1; in diesem Fall ist
E(Q) = hP = (2, 3)i
3. Die Gruppenstruktur
23
und r = 0 sowie T = E(Q) ≈ Z/6Z.
(ii) E : Y 2 = X 3 − X; diese Kurve besitzt über Q die Struktur
E(Q) = {O, (0, 0), (−1, 0), (+1, 0)};
hier ist der Rang r = 0 und T = E(Q) ≈ (Z/2Z) × (Z/2Z) (vgl. Satz
7 in §6).
(iii) E : Y 2 = X 3 − 4; hier ist
E(Q) = hP = (2, 2)i
und r = 1 und T = {O}.
Der Satz von Mordell besitzt weitreichende Verallgemeinerungen: Andre
Weil bewies 1929 ein entsprechendes Analogon für sogenannte ’abelsche Varietäten’: Gegeben ein beliebiger Zahlkörper K (also eine endliche algebraische
Erweiterung von Q), so ist die Gruppe der K-rationalen Punkte einer über K
definierten abelschen Varietät eine endlich erzeugte abelsche Gruppe — die so
genannte Mordell-Weil Gruppe.
Die Torsion ist besser verstanden als der Rang. Unabhängig voneinander
bewiesen Nagell und Lutz:
Satz 5 (Nagell 1935; Lutz 1937). Sei E eine elliptische Kurve mit definierender Gleichung Y 2 = X 3 + aX + b mit ganzzahligen Koeffizienten a und
b. Ist dann P = (x, y) ∈ T = Etors (Q) ein Torsionspunkt, so gilt x, y ∈ Z und
y 2 | (4a3 + 27b2 ) = −∆
falls
y 6= 0.
Da also die Diskriminante nur endlich viele Teiler haben kann, folgt also nun
noch einmal, dass es nur endlich viele Torsionspunkte geben kann; diesmal
jedoch mit einer expliziten Schranke für die ganzzahligen Koordinaten derselben! Insbesondere folgt für die Kardinalität der Torsionsgruppe
p
♯T ≤ 2 + 2 |∆|.
Ein tiefliegender Satz zeigt jedoch auf, dass erstaunlicherweise nur endlich viele
verschiedene Torsionsgruppen auftreten:
Satz von Mazur (1975). Für eine elliptische Kurve wie oben existieren nur
die folgenden fünfzehn Torsionstypen:
Etors (Q) ≃ Z/nZ
mit n ≤ 12, n 6= 11,
oder
Etors (Q) ≃ Z/2Z ⊕ Z/nZ
mit
n = 2, 4, 6, 8.
All diese Typen treten als Torsionsgruppen auf.
Der Beweis ist schwierig und wir verweisen auf den Originalartikel.† Wir diskutieren diesen Satz lediglich mit Blick auf unsere obigen Beispiele: In Beispiel i)
†
B. Mazur, Modular curves and the Eisenstein ideal, IHES Publ. Math. 47 (1977),
33-186.
24
ELLIPTISCHE KURVEN
ist die Diskriminante ∆ = −27 und für die y-Koordinate eines Torsionspunktes
kommen also nur 0, ±1, ±3 in Frage; die Torsionsgruppe ist hier T = Z/6Z.
Übrigens: Punkte mit ganzzahligen Koordinaten sind nicht notwendig Torsionspunkte! Ein Beispiel hierfür liefert die durch Y 2 = X 3 + 17 definierte
elliptische Kurve mit dem Punkt P = (−2, 3) unendlicher Ordnung. In diesem
Zusammenhang sei ein weiterer tiefliegender Satz erwähnt:
Satz von Siegel (1926). Für eine elliptische Kurve wie oben existieren nur
endlich viele Punkte mit ganzzahligen Koordinaten.
Hier verweisen wir für den Beweis auf [3]. Ein erstes Beispiel für solche Aussagen haben wir bereits in §1 mit der Ramanujanschen Gleichung U 3 +V 3 = 1729
kennen gelernt; der Satz von Siegel ist jedoch weitaus allgemeiner. Die Aussage
des Siegelschen Satzes ist übrigens falsch für singuläre kubische Kurven, wie
die Neilsche Parabel
Y 2 = X3
aufzeigt; hier lassen sich nämlich die Punkte mit ganzzahligen Koordinaten
durch (m2 , m3 ) mit m ∈ Z parametrisieren. Ferner zeigt dieses Beispiel, dass
auch die Aussage des Mordellschen Satzes falsch für singuläre kubische Kurven
ist.
4. Reduktion modulo p
Zahlentheoretische Probleme betrachtet man oft am besten mit der modularen Brille: Angenommen, wir fragen uns, welche Zahlen sich als Differenz von
zwei Quadratzahlen darstellen lassen, so sind dies u.a. die ungeraden Zahlen,
denn es gilt
2m + 1 = (m + 1)2 − m2 ;
auch findet man alle Vielfachen von 4 wieder (nämlich durch Multiplikation der
letzten Gleichung mit 4 = 22 ), nicht aber die Zahlen, die bei Division durch 4,
den Rest 2 lassen. Wie beweist man dies? Eine ganze Zahl ist entweder gerade,
d.h. von der Form n = 2k, oder ungerade, d.h. n = 2k +1. Entsprechend lassen
die Quadrate n2 = 4k2 bzw. 4k2 + 4k + 1 den Rest 0 oder 1 bei Division durch
4 und deshalb ist die Differenz zweier Quadratzahlen nie eine Zahl, die den
Rest 2 bei Division durch 4 lässt.
Arithmetische Obstruktionen äußern sich oft bei Blick auf die Primzahlen!
In dem obigen Beispiel ist es die Parität, also die Eigenschaft ob eine Zahl
gerade oder ungerade ist, welche Darstellungen als Differenz zweier Quadrate
erlaubt oder verbietet. Es ist also die Primzahl 2, die wir in diesem Fall zu
betrachten hatten (bzw. dessen Quadrat). Primzahlen sind die multiplikativen
Bausteine der ganzen Zahlen und jede ganze Zahl lässt sich bekanntlich bis
auf das Vorzeichen als im Wesentlichen eindeutiges Produkt von Primzahlpotenzen darstellen. Insofern bestimmen Primzahlen gewisse Teilbarkeitseigenschaften oder auch Darstellbarkeitsphänomene bei ganzen Zahlen!
4. Reduktion modulo p
25
In der arithmetischen Theorie der elliptischen Kurven (aber natürlich auch
im Hinblick auf kryptographische Anwendungen) ist insbesondere die Reduktion modulo Primzahlen von Interesse. Hierbei studiert man eine gegebene
elliptische Kurve
(5)
E : Y 2 = X 3 + aX + b
mit
a, b ∈ Z
über endlichen Körpern. Aus der Algebra ist bekannt, dass jeder endliche
Körper isomorph zu einer Erweiterung Fq eines primen Restklassenkörpers
Fp = Z/pZ ist; hierbei ist p eine Primzahl und bezeichne auch im Folgenden
stets eine Primzahl sowie q = pf für eine natürliche Zahl f . Mit Hilfe der
natürlichen Einbettung
N ֒→ Z/pZ,
n 7→ 1| + .{z
. . + 1}
n−mal
erklärt sich der kanonische Homomorphismus
Z → Z/pZ,
n 7→ n mod p
und entsprechend werden wir statt (5) die Kongruenz
(6)
E : Y 2 ≡ X 3 + aX + b mod p
studieren; dabei dürfen wir a, b als Elemente von Z/pZ auffassen. Nun definiert
diese Kongruenz eine Gleichung im Körper Z/pZ und insofern beschreibt (6)
eine Kurve über dem Restklassenkörper Z/pZ, welche wir mit E(Z/pZ) notieren und die Reduktion modulo p der primär über Z erklärten elliptischen
Kurve E nennen. (Tatsächlich untersucht man auch elliptische Kurven über
allgemeinen endlichen Körpern Fq , jedoch opfern wir diese Allgemeinheit der
Einfachheit.)
Nach dem Poincaréschen Satz 3 trägt die Reduktion E(Z/pZ) modulo einer
Primzahl p wieder die Struktur einer abelschen Gruppe und die Additionsgesetze erklären sich völlig analog zu denen über Q (s.u.); dabei spielt nach
wie vor ein unendlich ferner Punkt O die Rolle des neutralen Elementes bzgl.
dieser Addition. Ferner haben wir es bei elliptischen Kurven über endlichen
Körpern stets mit endlichen Gruppen zu tun (was sie insbesondere interessant
für kryptographische Aspekte macht).
Die wichtigsten Fragen mit Blick auf die Arithmetik elliptischer Kurven
sind bei dieser Konstruktion: Welche Eigenschaften erbt E(Z/pZ) von E(Q)
und welche Rückschlüsse von E(Z/pZ) auf E(Q) lassen sich ziehen?
Als ein Beispiel untersuchen wir die elliptische Kurve
E : Y 2 = X 3 + X,
welche nach §3 über den rationalen Zahlen die Struktur
E(Q) = {O, (0, 0)}
26
ELLIPTISCHE KURVEN
besitzt. Für die Diskussion der modulo einer Primzahl p reduzierten Kurven
haben wir also die Kongruenz
Y 2 ≡ X 3 + X mod p
zu studieren. Hierbei ist der kleine Satz von Fermat besonders wichtig: Für
p ∤ a gilt ap−1 ≡ 1 mod p bzw. ap ≡ a mod p.
• p = 2 : Mit dem kleinen Fermat vereinfacht sich die zu untersuchende
Kongruenz zu
Y ≡ Y 2 ≡ X 3 + X ≡ X + X ≡ 0 mod 2
und es ergibt sich {(0, 0), (1, 0)} als Menge der Punkte die, dieser Kongruenz
genügen, wobei wir noch gar nicht den unendlich fernen Punkt berücksichtigt
haben. Allerdings ist die Charakteristik des zu Grunde liegenden endlichen
Körpers zwei und in diesem Fall haben wir es (s.o.) nicht mit einer kubischen
Kurve zu tun; außerdem ergibt sich hier noch die Diskriminante als ∆ = −4 ≡
0 mod 2, weshalb wir es darüber hinaus auch noch mit einer singulären nichtkubischen Kurve zu tun haben und deshalb also das Gruppengesetz keinen
Sinn macht.
Wir fahren mit unserer Beispielkurve fort:
• p = 3 : In ähnlicher Weise findet man hier mit (0, 0), (2, 1), (2, 2) drei
endliche Punkte, jedoch ist hier die Charakteristik des endlichen Körpers drei
und also unsere Kurve wiederum keine kubische Kurve.
• p = 5 : In diesem Fall handelt es sich um eine nicht-singuläre kubische
Kurve und es gilt E(Z/5Z) = {O, (0, 0), (2, 0), (3, 0)}.
Wir sagen die elliptische Kurve E : Y 2 = X 3 +aX+b hat gute Reduktion
modulo p, falls die Kurve E(Z/pZ) nicht-singulär ist, also ∆ = −(4a3 +
27b2 ) 6≡ 0 mod p gilt; ansonsten sprechen wir von schlechter Reduktion
modulo p. Nun hat die Diskriminante ∆ nur endlich viele Primteiler, d.h. für
alle bis auf endlich viele Primzahlen ist die Reduktion gut.
Und noch ein Beispiel:
E : Y 2 = X3 − 2
über Z/5Z.
Hier berechnet sich die Diskriminante als ∆ = −22 · 33 . Modulo p = 5 haben
wir also gute Reduktion und es zeigt sich
E(Z/5Z) = {O, (1, 2), (1, 3), (2, 1), (2, 4), (3, 0)}.
Diese elliptische Kurve besteht also aus sechs Punkten. Um mehr Einsicht in
die Struktur dieser Gruppe zu erhalten, schauen wir uns an, wie sich Vielfache
des Punktes P = (1, 2) verhalten. Mit dem Gruppengesetz aus §3 ergibt sich
für die Koordinaten des Punktes 2P = P ⊕ P = (x3 , −y3 )
x3 = (3x21 + a)2 (2y1 )−2 − 2x1 ,
y3 = (3x21 + a)(2y1 )−1 (x3 − x1 ) + y1 ,
4. Reduktion modulo p
27
wobei in unserem Fall a = 0 gilt; dabei haben wir jeweils das multiplikativ
Inverse im Körper Z/5Z zu nehmen. Speziell mit x1 = 1, y1 = 2 ergibt sich
daraus
x3 = (3 · 4−1 )2 − 2 ≡ 2,
y3 = 3 · 4−1 (2 − 1) + 2 ≡ 4 ≡ −1 mod 5,
also 2P = (2, 1). (Spiegeln an der x-Achse nicht vergessen!) Mit noch ein wenig
mehr Rechnerei ergibt sich
P = (1, 2) → 2P = (2, 1) → 3P = (3, 0) →
→ 4P = (2, 4) → 5P = (1, 3) → 6P = O,
womit also der Punkt P die Gruppe erzeugt. Im Falle 6P = 3P ⊕ 3P entsteht
der unendlich ferne Punkt, denn bei der Addition ist hier das Inverse von
0 mod 5 zu berechnen, was wir ähnlich zum rationalen Fall als ∞ deuten.
Abbildung 15. Eine Visualisierung der elliptischen Kurve Y 2 = X 3 −
2 bei Reduktion modulo p = 5. Die Gruppe ist zyklisch von der Ordnung
sechs.
Von großer Wichtigkeit ist die Größe von elliptischen Kurven über endlichen
Körpern. Bezeichnet
N (p) := ♯E(Z/pZ)
die Gruppenordnung der Reduktion modulo p, so gilt sicherlich
1 ≤ N (p) ≤ 2p + 1,
denn stets ist O ∈ E(Z/pZ), was die erste Ungleichung liefert, während die
zweite Ungleichung daraus resultiert, dass für jede der p Restklassen x mod p
es höchstens zwei y mit y 2 ≡ x3 + ax + b mod p gibt (da Z/pZ ein Körper ist).
28
ELLIPTISCHE KURVEN
Tatsächlich gilt jedoch etwas viel Restriktiveres, was wir mit einem heuristischen Argument plausibel machen wollen: Aus der Theorie der quadratischen
Reste ist bekannt, dass es genauso viele quadratische Reste wie Nichtreste
modulo p gibt, wobei p hier und im Folgenden eine ungerade Primzahl sei.
(Wir erinnern: a 6≡ 0 mod p ist ein quadratischer Rest, wenn die Kongruenz
X 2 ≡ a mod p lösbar ist; ansonsten heißt a ein Nichtrest. Mehr hierzu findet
sich in jedem Zahlentheoriebuch wie etwa [6].) Dies interpretieren wir so, dass
zu x ∈ {0, 1, . . . , p − 1} die Wahrscheinlichkeit, dass x3 + ax + b ein Quadrat
ist, gleich 21 beträgt. Also ist der Erwartungswert für N (p) gleich
1+2·
1
2
· p = p + 1.
Es geht noch etwas genauer: Das Legendre-Symbol beschreibt, ob eine Restklasse ein quadratischer Rest ist oder nicht:

 +1, wenn a mod p quadratischer Rest,
a
=
0 , falls p | a,

p
−1, wenn a mod p quadratischer Nichtrest.
Damit schreibt sich
3
X x3 + ax + b X x + ax + b
= p+1+
;
N (p) = 1 +
1+
p
p
x mod p
x mod p
hier ist jeder Summand entweder gleich zwei oder gleich null, je nachdem,
ob (x, y) ∈ E(Z/pZ). Da das Legendre-Symbol ausschließlich die Werte 0, ±1
annimmt, liegt es nahe die Summe rechts als eine stochastische Irrfahrt zu
interpretieren (was sie sicherlich nicht ist); mit der Theorie der Irrfahrten
√
(bzw. dem Satz von Moivre-Laplace) ist der Wert der Summe als O( p) zu
schätzen. Tatsächlich liefert dies die richtige Größenordnung, wie bereits Emil
Artin vermutete und Helmut Hasse bewies:
Satz 6 (Hasse 1933). Sei p prim und E eine elliptische Kurve über Z/pZ,
dann gilt
√
|p + 1 − N (p)| < 2 p.
Der Satz von Hasse gilt auch für elliptische Kurven über endlichen Körpern
Fq , bloß ist hier die Ungleichung des Satzes zu ersetzen durch
√
|q + 1 − N (q)| ≤ 2 q.
Auch dieses Ergebnis wurde von Weil (1948) auf beliebige nicht-singuläre Kurven verallgemeinert; auf ihn zurückgehende höherdimensionale Vermutungen
über die Anzahl von Punkten auf algebraischen Varietäten über endlichen
Körpern wurden von Dwork, Grothendieck und Deligne (1974) bewiesen; Pierre Deligne wurde für seine Arbeiten 1978 mit der Fields-Medaille ausgezeichnet.
Wir wollen einen Spezialfall des Satzes 6 von Hasse beweisen. Ein Blick in
die Liste der ersten Gruppenordnungen der durch die Gleichung Y 2 = X 3 + X
4. Reduktion modulo p
29
Abbildung 16. Helmut Hasse, ∗ 1898 in Kassel, - † in Ahrensburg
bei Hamburg; bedeutender Mathematiker, der hauptsächlich zur algebraischen Zahlentheorie arbeitete und das ’Lokal-Global-Prinzip’ für quadratische Formen entdeckte. Rechts: André Weil, ∗ 1906 in Paris, - † 1998
in Princeton; weltreisende Berühmtheit und Bourbaki-Mitglied mit einem
bewegten Lebenslauf und sehr tiefliegenden Ergebnissen in algebraischer
Geometrie und Zahlentheorie.
definierten Kurve bei Reduktion modulo kleiner Primzahlen offenbart eine
gewisse Gesetzmäßigkeit:
5 7 11 13 17 19 23 29
p
N (p) 4 8 12 20 16 20 24 20
Offensichtlich gilt hier:
für jede Primzahl p ≡ 3 mod 4.
N (p) = p + 1
Beweis. Mit dem ersten Ergänzungsgesetz (siehe etwa [6]),
p−1
−1
= (−1) 2 = −1,
p
zeigt sich (zusammen mit den Rechenreglen für das Legendre-Symbol)
(−x)3 + (−x)
−(x3 + x)
=
p
p
3
3
x +x
x +x
−1
=−
.
=
p
p
p
Also folgt
0 =
X
06≡x mod p
= 2
X
06≡x mod p
(−x)3 + (−x)
p
3
x +x
,
p
+
x3 + x
p
30
ELLIPTISCHE KURVEN
denn mit x durchläuft auch −x alle primen Restklassen modulo p. Es folgt
also N (p) = p + 1. •
In diesem Beweis eines wirklich einfachen Spezialfalles des Satzes von Hasse
haben wir eine Symmetrie der elliptischen Kurve E : Y 2 = X 3 −X ausgenutzt,
die nicht alle elliptische Kurven teilen. Neben den üblichen Endomorphismen
der Multiplikation mit einer ganzen Zahl,
E → E,
P 7→ n · P = P
. . ⊕ P}
| ⊕ .{z
n−mal
für n ∈ Z,
besitzt diese spezielle elliptische Kurve den zusätzlichen Endomorphismus
√
ψ : E → E, (x, y) 7→ (−x, y −1),
√
wobei −1 hier für eine primitive vierte Einheitswurzel steht (also im komplexen Fall gleich der imaginären Einheit ist); eine solche zusätzliche Symmetrie
nennt man komplexe Multiplikation, manifestiert sich diese doch stets als
ein Element eines Ganzheitsrings eines imaginär-quadratischen Zahlkörpers
(siehe [11]).
Bei der Kurve gegeben durch die Gleichung Y 2 = X 3 + 17 bei Reduktion modulo Primzahlen p ≡ 2 mod 3 erhält man mit einem ganz ähnlichen
Argument ebenfalls N (p) = p + 1.
Von besonderem Interesse ist auch die Frage, inwieweit sich lokale Information für globale Fragen nutzbar machen lässt. Hierzu sei zunächst der berühmte
Satz von Hasse–Minkowski über nicht-triviale Darstellungen rationaler Zahlen durch über Q definierte quadratische Formen erwähnt, welcher zeigt, dass
jene äquivalent zur nicht-trivialen Darstellbarkeit in allen lokalen p-adischen
Körpern Qp zuzüglich R ist (siehe [9]). Ein einfaches Beispiel für diese geheimnisvolle Beziehung,
globale Information
ist:
x ist ein rationales Quadrat
←→
lokale Information ,
x ist ein Quadrat über den reellen Zahlen und modulo allen Primzahlen.
Es ist bekannt, dass diese ebenfalls auf Hasse zurückgehende Idee, das so
genannte Lokal-Global-Prinzip, also lokale Informationen aus den p-adischen
Vervollständigungen des globalen Körpers Q für die Arithmetik von Q zu gewinnen, bereits für kubische Formen i.A. scheitert. Allerdings mag man im
Falle elliptischer Kurven hoffen, trotzdem ein Analogon dieser Idee zu finden:
Betrachten wir beispielsweise die Kurve zur Gleichung
⇐⇒
E : Y 2 = X3 − 2
von oben, so ist (3, 5) ∈ E(Q) ein rationaler Punkt und bei Reduktion modulo p folgt (3, 5) ∈ E(Z/pZ) für alle Primzahlen p guter Reduktion. (Hier
nutzen wir nur aus, dass Kongruenzen gewissermaßen Abschwächungen der
Gleichheitsrelation sind!) Wir fragen: Gilt auch die Umkehrung? Genauer:
5. Assoziativität des Gruppengesetzes
31
Gibt es ’relativ viele’ Punkte in ’vielen’ Kurven E(Z/pZ),
so sollten sich viele von diesen zu rationalen Punkten auf
E(Q) zusammenfügen!
Und dies wäre letztlich ein Indiz dafür, dass E(Q) unendlich viele Punkte
enthält. Es geht hier also wie beim Satz von Hasse–Minkowski um das Schlagen einer Brücke zwischen lokaler und globaler Information (d.h. Punkte bei
Reduktion modulo Primzahlen vs. rationale Punkte). Tatsächlich steht hier
im Hintergrund eine der sieben Millennium-Vermutungen, die offene
Vermutung von Birch & Swinnerton–Dyer (1963/65). Ist E eine über
Z definierte elliptische Kurve, so gilt
Y N (p)
πE (x) :=
∼ CE (log x)rg(E)
p
p≤x
mit einer nur von E abhängigen Konstanten CE 6= 0 bei x → ∞.
Dies ist eine schwache Form der Vermutung von Birch & Swinnerton–Dyer;
eine stärkere Version wird uns später noch beschäftigen. Ist also die Gruppenordnung N (p) bei Reduktion modulo p für viele Primzahlen signifikant größer
als der Erwartungswert, so sollte der Rang der Kurve rg(E) positiv sein. Numerische Daten für viele elliptische Kurven unterstützen diese Vorhersage.
5. Die Assoziativität des Gruppengesetzes
Für den vollständigen Beweis des Poincaréschen Satzes 3 fehlt nur noch
der Nachweis der Assoziativität bei der Addition von Punkten, also
(P ⊕ Q) ⊕ R = P ⊕ (Q ⊕ R)
für beliebige endliche Punkte P, Q, R auf einer elliptischen Kurve E(K) mit
einem fixierten Körper K. Hierfür gibt es verschiedene Beweise: Ein eleganter
Ansatz benutzt Divisoren und den Satz von Riemann-Roch aus der algebraischen Geometrie, die wir hier nicht voraussetzen wollen. Am einfachsten ist
vielleicht der komplexe Beweis, welcher allerdings den Makel hat, das Gruppengesetz nur für C und Teilkörper zu liefern. Wir möchten Satz 3 jedoch für
beliebige Körper (insbesondere für die in der Kryptographie so wichtigen endlichen Körper) vollständig beweisen.‡ Dazu machen wir einen kurzen Abstecher
in die projektive Geometrie (vgl. auch §1).
Gegeben ein Körper K, betrachten wir die zugehörige projektive Ebene
P2 (K) = (K3 \ {0})/ ∼,
wobei die Quotientenstruktur durch die Äquivalenzrelation
(x, y, z) ∼ (λx, λy, λz)
für λ ∈ K∗
entsteht. Damit werden alle skalaren Vielfachen eines Vektors (x, y, z) miteinander identifiziert und wir notieren die Äquivalenzklassen als (x : y : z).
‡
Prinzipiell könnte man sich auch einen Beweis mittels Computer-Algebra vorstellen...
32
ELLIPTISCHE KURVEN
Jede Gerade durch den Ursprung 0 in K3 steht also für einen Punkt in der
projektiven Ebene. Aus der affinen Kurve enststeht die zugehörige projektive
Kurve durch ’Homogenisierung’
affine elliptische Kurve:
Y 2 = X 3 + aX + b
−→
projektive elliptische Kurve:
Y 2 Z = X 3 + aXZ 2 + bZ 3 .
Offensichtlich genügen mit (x, y, z) auch λ(x, y, z) der homogenisierten projektiven Gleichung. Die projektive Kurve enthält den zusätzlichen Punkt (0 : 1 :
0), welchen wir als den unendlich fernen Punkt O auffassen. Die affine Kurve gewinnt man aus der projektiven Kurve einfach durch Projektion Z = 1
zurück. Ferner stellt sich ein affiner Punkt P = (x, y) auf der projektiven
Kurve dar als
(x : y : 1) = ( xy : 1 : y1 )
und mit y, x → ∞ ergibt sich der unendlich ferne Punkt O.
Eine affine Kurve C, gegeben durch eine polynomielle Gleichung P (X, Y ) =
0, heißt bekanntlich irreduzibel, falls das Polynom P irreduzibel ist, sich also
nur trivial faktorisieren lässt. Projektive Kurven C1 und C2 besitzen keine gemeinsame Komponente, wenn ihre irreduziblen Komponenten verschieden
sind, also kein gemeinsamer polynomieller Faktor (von einem positiven Grad)
in beiden definierenden Polynomen aufgeht. Insbesondere ist der Schnitt zweier solcher Kurven notwendig eine endliche Punktmenge und wir definieren für
einen Punkt P ∈ C1 ∩ C2 die Schnittmultiplizität als
ı(C1 ∩ C2 , P ) = 1,
falls C1 und C2 sich transversal in P schneiden, bzw. als ı(C1 ∩ C2 , P ) = m,
wenn die Vielfachheit m ist (und natürlich null für P ∈
6 C1 ∩ C2 ). Damit
formuliert sich nun der
Satz von Bezout. Für zwei projektive Kurven C1 und C2 ohne gemeinsame
Komponenten gilt
X
ı(C1 ∩ C2 , P ) = deg C1 · deg C2 .
P ∈C1 ∩C2
Sind C1 und C2 beide glatt ohne nicht transversale Schnitte, so gilt
♯(C1 ∩ C2 ) = deg C1 · deg C2 .
Insbesondere schneiden sich zwei parallele Geraden im Unendlichen (denn Geraden haben Grad deg C = 1; man erinnere sich an die Definition des Grades
in §1). Ferner zeigt sich, wie bereits erwähnt, dass eine Gerade eine elliptische
Kurve stets in genau drei Punkten schneidet. Für einen Beweis des Bezoutschen Satzes verweisen wir auf [4] bzw. [8].
Neunpunktesatz. Seien C, C1 und C2 drei kubische Kurven und C enthalte
acht der neun Schnittpunkte von C1 ∩ C2 , dann liegt auch der neunte Schnittpunkt auf C.
5. Assoziativität des Gruppengesetzes
33
Abbildung 17. Die Assoziativität der Addition von Punkten auf einer
elliptischen Kurve; das Bild ist dem schönen Buch [8] entnommen, weshalb
hier auch’+’ statt ’⊕’ steht.
Der Beweis funktioniert so ähnlich, wie die für folgende Sätze der analytischen
Geometrie: Durch zwei verschiedene Punkte im Euklidischen geht genau Gerade; oder höherdimensional: Eine Quadrik in allgemeiner Lage ist durch fünf
Punkte eindeutig bestimmt.
34
ELLIPTISCHE KURVEN
Beweis. Eine projektive kubische Kurve ist gegeben durch eine kubische Gleichung der Form
aX 3 +bX 2 Y +cXY 2 +dY 3 +eX 2 Z +f XZ 2 +gY 2 Z +hY Z 2 +iZ 3 +jXY Z = 0.
Jede solche kubische Kurve C ist also durch die zehn Koeffizienten a, b, c, . . . , i, j
bestimmt; Multiplikation der Gleichung mit einem von null verschiedenen Skalar verändert nicht die Kurve. Also ist C bis auf ein Vielfaches der Koeffizienten
eindeutig bestimmt, definiert also einen eindeutigen Punkt (a : b : c : . . . : i : j)
im projektiven Raum P9 (den man analog zum P2 definiert). Darüberhinaus
ist die Menge aller kubischen Kurven isomorph zum P9 . Nun fragen wir, wann
ein Punkt P = (x : y : z) auf einer kubischen Kurve C liegt. Dies ist genau
dann der Fall, wenn die lineare homogene Gleichung
ax3 + bx2 y + cxy 2 + dy 3 + ex2 z + f xz 2 + gy 2 z + hyz 2 + iz 3 + jxyz = 0.
in den unbekannten Koeffizienten a, b, c, . . . , i, j erfüllt ist. Also ist für einen
gegebenen Punkt P die Menge aller Kurven C, die P enthalten, durch eine homogene lineare Gleichung in P9 determiniert. Entsprechend ist die Menge aller
Kurven C, welche die n verschiedenen Punkte P1 , . . . , Pn enthalten, eindeutig
durch ein System von n homogenen linearen Gleichungen in P9 festgelegt.
Haben wir also zwei kubische Kurven C1 , C2 mit mindestens neun gemeinsamen Punkten gegeben, so sei C die Menge aller kubischen Kurven C, welche
durch irgendwelche fest gewählten acht der neun Punkte laufen. Diese Menge
korrespondiert mit einer Lösung eines Systems von acht homogenen linearen
Gleichungen in zehn Unbekannten. Der Lösungsraum besteht nun aus allen
Linearkombinationen λ1 v + λ2 w zweier linear unabhängiger Lösungen v, w
von Zehntupeln. Da nun sowohl C1 als auch C2 in C enthalten sind, liefern die
Koeffizienten ihrer definierenden Gleichungen F1 = 0 bzw. F2 = 0 jeweils ein
Zehntupel, welches dieses homogene lineare Gleichungssystem löst und deshalb
den gesamten Lösungsraum aufspannen. Ist nun C eine weitere kubische Kurve
in C, die also jene ausgezeichneten acht Punkte trifft, so ist die C definierende
Gleichung von der Form
λ1 F1 (X, Y, Z) + λ2 F2 (X, Y, Z) = 0
für gewisse
λ1 , λ2 ∈ K.
Damit enthält aber C sicher auch den neunten Punkt (x : y : z) (denn für
jenen gilt Fj (x, y, z) = 0). •
Damit gelingt nun der Beweis der Assoziativität wie folgt: Gegeben seien
P, Q, R ∈ E(K), dann bezeichnen P ∗ Q und Q ∗ R den dritten Schnittpunkt
der Sekante durch P und Q bzw. durch Q und R mit der elliptischen Kurve
E(K); im Falle P = Q bzw. Q = R handelt es sich dabei um die Tangente.
Auf jeden Fall existiert jedoch dieser dritte Schnittpunkt dank des Satzes von
Bezout. Können wir
(7)
(P ⊕ Q) ∗ R = P ∗ (Q ⊕ R)
6. Fermats ’descente infinie’
35
zeigen, so folgt bereits
(P ⊕ Q) ⊕ R = P ⊕ (Q ⊕ R)
und damit die Assoziativität des Gruppengesetz. Dabei haben wir gewissermaßen O gekürzt, denn aus der Definition der Addition folgt
P ⊕ Q = O ∗ (P ∗ Q).
Wir notieren eine Gerade beispielsweise durch die Punkte P und Q nun
kurz mit P Q. Wir starten mit den Geraden P (Q ⊕ R) (die durgezogene Linie
in Abbildung 17) und (P ⊕ Q)R (gestrichelt in Abbildung 17). Wir haben zu
zeigen, dass deren Schnitt auf der elliptischen Kurve liegt. In dem Falle folgt
nämlich (7). Hierzu betrachten wir die neun Punkte
•
•
•
•
O, P, Q, R,
P ∗ Q, P ⊕ Q,
Q ∗ R, Q ⊕ R, sowie
den Schnittpunkt beider Geraden.
Nun definieren die drei Geraden RQ sowie P (Q ⊕ R) und (P ⊕ Q)(P ∗ Q)
als jeweils lineare Gleichung (die jeweils durchgezogenen Linien) eine kubische Kurve C1 . Analog definieren die drei Geraden P Q sowie R(P ⊕ Q) und
(Q ⊕ R)(Q ∗ R) (die jeweils gestrichelten Linien) eine kubische Kurve C2 . Nach
Konstruktion liegen die neun Punkte auf beiden kubischen Kurven. Unsere
elliptische Kurve E trifft acht dieser Punkte des Schnittes C1 ∩ C2 und nach
dem Neunpunktesatz liegt dann auch der neunte Punkt, der Schnittpunkt der
Geraden P (Q⊕R) und (P ⊕Q)R, auf der elliptischen Kurve. Dies zeigt (7) und
letztlich also die Assoziativität der Punkteaddition auf elliptischen Kurven. •
6. Fermats ’descente infinie’
Pierre de Fermat las Bachets lateinische Übersetzung Diophants ’Arithmetica’ und notierte auf dem sehr schmalen Rand neben Euklids Parametrisierung der pythagoräischen Tripel (Satz 1), dass er für die Unmöglichkeit eines
analogen Resultates mit Kuben oder Biquadraten oder gar höheren Potenzen
statt der Quadrate einen wunderbaren Beweis besitze (siehe §1).
Fermat’s last theorem. [Andrew Wiles, 1995] Die Gleichung
Xn + Y n = Zn
mit
n≥3
besitzt nur triviale Lösungen in ganzen Zahlen, d.h. xyz = 0.
Wiles gefeierter Beweis basiert auf der Theorie der Modulformen und elliptischen Kurven. Tatsächlich bewies Wiles einen Spezialfall der so genannten
’Shimura-Taniyama-Vermutung’ (aus dem Jahre 1957), welche eine Brücke
zwischen eben diesen Gebieten spannt. Die Idee, auf diese Art und Weise die
Fermatsche Vermutung zu beweisen (im Englischsprachigen auch ’Fermats last
theorem’ genannt, weil es lange das letzte unbewiesene Resultat aus Fermats
Briefen an seine Zeitgenossen war), geht zurück auf Hellegouarch und Frey,
36
ELLIPTISCHE KURVEN
Abbildung 18. Oben: Yutaka Taniyama, ∗ 1927 - † 1958 in Tokio
(links) und Goro Shimura, ∗ 1930 in Hamamatsu (rechts); unten: Andrew
Wiles, ∗ 1953 in Cambridge. Das erste Indiz für die Richtigkeit der bemerkenswerten Shimura-Taniyama-Vermutung aus dem Jahre 1955 war Weils
Umkehrsatz von 1967.
die beide (unabhängig voneinander) in den siebziger Jahren folgenden Ansatz
proklamierten: Angenommen, es gäbe eine nicht-triviale Lösung der FermatGleichung für ein festes n ≥ 3,
(8)
xn + y n = z n ,
so betrachte man die elliptische Kurve
E : Y 2 = X(X − xn )(X − z n )
mit der nach unserer Annahme nicht verschwindenden Diskriminante ∆ =
16(xyz)2n . Hier ist E zwar noch nicht in Weierstraßscher Normalform gegeben, lässt sich aber leicht in diese transformieren. Bei der Berechnung der
Diskriminante legt man am besten die algebraische Definition als Produkt der
Quadrate über die Differenzen der Nullstellen zu Grunde und berechnet mit
Hilfe von (8)
∆ = 16(xn )2 (z n − xn )2 (z n )2 = 16x2n y 2n z 2n .
Die Idee ist nun, zu zeigen, dass diese so definierte elliptische Kurve nicht modular sein kann, also bei Reduktion modulo Primzahlen nicht von so genannten
6. Fermats ’descente infinie’
37
Modulformen herrührt (was von Ribet um 1990 bewiesen wurde). Tatsächlich
besagt die mittlerweile von Wiles et al. komplett bewiesene Shimura-TaniyamaVermutung, dass alle über den rationalen Zahlen definierten elliptischen Kurven von gewissen Modulformen herrühren. Wiles genügte ursprünglich ein Spezialfall dieser Vermutung um Fermats ’letzten Satz’ auf folgendem Umweg zu
beweisen: Wenn Fermats letzter Satz falsch ist, so auch die Taniyama-ShimuraVermutung; ist die Taniyama-Shimura-Vermutung hingegen richtig, so muss
auch Fermats letzter Satz richtig sein!§
Wir kehren zurück zu Fermat. Sicher ist, dass er einen Beweis für den Exponenten n = 4 hatte und womöglich glaubte Fermat, dass seine Beweismethode – die Methdode des unendlichen Abstiegs (descente infinie) – für beliebige
Exponenten n ≥ 3 anwendbar sei. Allerdings bereitet bereits n = 3 Probleme, welche Euler teilweise und schließlich Gauß gänzlich behoben. Es scheint
jedoch aussichtslos, den allgemeinen Fall mit elementaren Methoden zu behandeln. Hier geben wir nun Fermats Argument für den Exponenten n = 4 im
Gewand elliptischer Kurven:
Satz 7. Die elliptische Kurve
E : Y 2 = X3 − X
besitzt über Q Rang null, enthält also nur ’triviale’ Punkte, d.h.
E(Q) = {O, (0, 0), (−1, 0), (1, 0)}.
Bevor wir diesen Satz beweisen, zeigen wir, dass hieraus tatsächlich die Gültigkeit der Fermatschen Vermutung für n = 4 folgt: Angenommen, es gibt eine
nicht-triviale Lösung, also x4 + y 4 = z 4 mit o.B.d.A. x, y, z ∈ N. Dann folgt
äquivalent x4 = z 4 − y 4 bzw. nach Multiplikation mit z 2 y −6
2 2 2 3
z
z2
x z
=
−
.
y3
y2
y2
Also folgte die Existenz eines rationalen Punktes auf der elliptischen Kurve
mit nichtverschwindender y-Koordinate, ein Widerspruch zu Satz 7.
Für den elementaren Beweis von Satz 7 bemühen wir Fermats Idee des
’descente infinie’. Ein wichtiges Hilfsmittel ist hierbei eine Größe, die wir später
(in §7) auch bei Mordell finden! Gilt α = ab ∈ Q mit gekürzten Zähler und
Nenner, so sei die Höhe von α 6= 0 definiert durch
H(α) := max{|a|, |b|}
und
H(0) := H( 10 ) = 1.
Die Fermatsche Beweisidee lässt sich nun kurz so formulieren:
Erziele einen Widerspruch durch Abstieg von einer ’kleinsten’ Lösung bzgl. der Höhe zu einer noch kleineren!
§
Einstiegsliteratur bietet der lesenswerte Artikel ’Über die Fermat-Vermutung’, Elem.
Math. 50 (1995), 12-25, von J. Kramer, mehr Details bietet [11]; in beiden Quellen finden
sich auch Zitate für die Originalarbeiten von Wiles et al.
38
ELLIPTISCHE KURVEN
Abbildung 19. Die elliptische Kurve Y 2 = X 3 −X mit ihren drei endlichen rationalen Punkten (0, 0), (±1, 0), welche man sofort aus der Faktorisierung Y 2 = (X − 1)X(X + 1) abliest.
Wir starten mit einigen Vorüberlegungen. Ist (0, 0) 6= (x, y) ein Punkt auf
E(Q), so auch (− x1 , xy2 ) denn insbesondere ist x 6= 0 und
y 2 −1 3 −1
−
⇐⇒
y 2 = −x + x3 .
=
x2
x
x
Wir gehen nun von einem Punkt (x1 , y1 ) ∈ E(Q) ungleich den trivialen
Punkten (0, 0), (±1, 0) aus. Dann ist
(x1 − 1)x1 (x1 + 1) = y12 > 0.
Wegen H(x) = H(− x1 ) dürfen wir annehmen, dass x1 > 1. Wir zeigen zuerst:
x1 − 1, x1 , x1 + 1 sind allesamt Quadrate rationaler Zahlen.
Sei also x1 = m
n mit teilerfremden natürlichen Zahlen m, n. Angenommen,
m und n sind ungerade, so folgt
x1 + 1
(m + n)/2
=
,
x1 − 1
(m − n)/2
x′1 =
wobei jeweils (m ± n)/2 ∈ Z. Nach einer langweiligen Rechnerei,
2
x1 + 1 3 x1 + 1
2y1
=
−
(x1 − 1)2
x1 − 1
x1 − 1
⇐⇒
4y12
folgt damit
=
(x1 + 1)(x1 − 1){(x1 + 1)2 − (x1 − 1)2 },
x′1 ,
2y1 ∈ E(Q).
(x1 − 1)2
6. Fermats ’descente infinie’
39
Nun ist
nm + n m − no
< max{m, n} = H(x1 ).
,
2
2
Setzen wir die natürliche Zahl H(x1 ) als minimal voraus, so ergibt sich ein
Widerspruch!
Also ist m gerade oder n gerade, aber nicht beide (da diese ja teilerfremd
sind). Eine einfache Rechnung zeigt
H(x′1 ) ≤ max
(m − n)mn(m + n)
,
n4
ein Quadrat! Nun sind die Zahlen m − n, m, n, m + n paarweise teilerfremd;
eigentlich bereitet nur der Fall m + n, m − n etwas Kopfzerbrechen. Wegen
y12 = (x1 − 1)x1 (x1 + 1) =
2m = (m + n) + (m − n)
und
2n = (m + n) − (m − n)
kommen hier als größter gemeinsamer Teiler nur 1 oder 2 in Frage, wobei
letzteres aber auf Grund der Teilerfremdheit von m und n unmöglich ist.
Mit der eindeutigen Primfaktorzerlegung (in Q) sind also alle Zahlen m −
n, m, n, m + n Quadrate rationaler Zahlen. Insbesondere gilt dies für
m
m+n
m−n
, x1 = , x1 + 1 =
,
x1 − 1 =
n
n
n
was zu zeigen war.
Diese Konstellation von drei Quadraten ist etwas besonderes, wie der folgende wichtige Satz zeigt, der Aufschluss über die Teilbarkeit eines Punktes
durch zwei gibt:
Satz 8 (’Multiplication by 2’-map). Sei K ein Körper einer Charakteristik
6= 2, 3 und
E : Y 2 = (X − α)(X − β)(X − γ)
mit paarweise verschiedenen Wurzeln α, β, γ ∈ K eine elliptische Kurve. Dann
gibt es zu jedem Punkt (x1 , y1 ) ∈ E(K) genau dann einen Punkt (x0 , y0 ) ∈
E(K) mit 2(x0 , y0 ) = (x1 , y1 ), wenn x1 − α, x1 − β, x1 − γ Quadrate in K sind.
Beweis. Wir nehmen an, dass (x1 , y1 ) = 2(x0 , y0 )(:= (x0 , y0 ) ⊕ (x0 , y0 )). Sei
Y = mX+b die Tangente an (x0 , y0 ) ∈ E(K), dann genügen die Punkte (x0 , y0 )
und (x1 , −y1 ) (Spiegeln an der x-Achse nicht vergessen!) der Gleichung
(X − α)(X − β)(X − γ) = (mX + b)2
bzw.
(X − α)(X − β)(X − γ) − (mX + b)2 = (X − x1 )(X − x0 )2
(dabei steht der Exponent zwei rechts beim Linearfaktor X − x0 , weil wir es
ja mit der Tangente zu tun haben). Im Folgenden bezeichne ein Quadrat in
K (nicht notwendig dasselbe bei jedem Auftreten). Dann ergibt sich speziell
für X = α
− = (α − x1 ) 6= 0
⇐⇒
x1 − α = sowie analog x1 − β, x1 − γ = mit paarweise verschiedenen Quadraten.
40
ELLIPTISCHE KURVEN
Für die Umkehrung sei nach einer etwaigen Variablentransformation o.B.d.A.
x1 = 0, dann gilt
y12 = −αβγ = t
für ein t ∈ K. Zusammen mit −α = α21 , −β = β12 , −γ = γ12 für gewisse
α1 , β1 , γ1 ∈ K (nach Voraussetzung) ergibt sich bei geeigneter Wahl der Vorzeichen
y1 = α1 β1 γ1 .
Damit bilden wir nun die Tangente Y = mX + y1 an den unbekannten Punkt
(x0 , y0 ) durch (0, y1 ) und erhalten durch Einsetzen
(X − α)(X − β)(X − γ) − (mX + y1 )2 = X(X − x0 )2 .
Setzen wir
(X − α)(X − β)(X − γ) = X 3 + rX 2 + sX + t,
so gilt
r = −α − β − γ,
(9)
s = αβ + αγ + βγ
Zusammen mit y1 = α1 β1 γ1 folgt oben also
3
1
X (X
+ rX 2 + sX + t − m2 X 2 − 2my1 X − y12 ) = (X − x0 )2 .
Ein Koeffizientenvergleich liefert t = y12 und die Diskriminante des quadratischen Polynoms
(10)
X 2 + (r − m2 )X + s − 2my1
verschwindet also (auf Grund der doppelten Nullstelle x0 ), d.h.
(11)
(r − m2 )2 = 4(s − 2my1 ).
Letzteres ist eine biquadratische Gleichung in m und wir suchen eine Lösung
in K, um einen Punkt (x0 , y0 ) mit Koordinaten in K zu finden! Mit Blick auf
die Cardanosche Formel spendieren wir eine Unbekannte u und fragen, wann
(m2 − r + u)2 = 2um2 − 8y1 m + (u2 − 2ru + 4s)
ein Quadrat ist? (Hierbei haben wir gegenüber (11) lediglich Null addiert.)
Nun soll das quadratische Polynom in m auf der rechten Seite eine doppelte
Nullstelle besitzen, entsprechend setzen wir dessen Diskriminante gleich Null:
0 = 64y12 − 8u(u2 − 2ru + 4s)
bzw. mit ein wenig Rechnerei und (9)
0 = u3 − 2ru2 + 4su − 8y12 = (u + 2α)(u + 2β)(u + 2γ).
Setzen wir also u = −2α, ergibt sich
(m2 − r − 2α)2 = −4αm2 − 8y1 m + (4α2 + 4rα + 4s)
und nach Substitution von (9) folgt
(m2 − α + β + γ)2 = 4(α1 m − β1 γ1 )2
7. Der Satz von Mordell
41
bzw.
m = ±α1 ± (β1 ∓ γ1 ).
Damit besitzt (11) wie gewünscht eine Lösung m0 ∈ K und, wie man sofort
nachrechnet, ist x0 = 21 (m20 − r) eine doppelte Nullstelle des Polynoms (10)
bzw. ebenso von
(X − α)(X − β)(X − γ) − (mX + y1 )2 .
Es folgt 2(x0 , −m0 x0 − y1 ) = (0, y1 ) und der Satz ist bewiesen. •
Nun geben wir den
Beweis von Satz 7. Hierzu wenden wir Satz 8 mit α = 1, β = 0 und γ = −1
an. Nach unseren Vorüberlegungen sind die Voraussetzungen von Satz 8 erfüllt
und somit existiert zu einem gegebenen Punkt (x1 , y1 ) auf E ein weiterer
(x0 , y0 ) mit 2(x0 , y0 ) = (x1 , y1 ). Es genügt nun zu zeigen, dass H(x0 ) < H(x1 )
gilt, denn dann ergibt sich der gewünschte Widerspruch unter Annahme der
Minimalität von H(x1 ).
Mit der Verdopplungsformel (dem Gruppengesetz bei Tangenten) zeigt sich
für x0 = ab mit teilerfremden a, b nach einer kleinen Rechnerei
x1 =
(a2 + b2 )2
(x20 + 1)2
=
.
4ab(a2 − b2 )
4(x30 − x0 )
Hier ist der größte gemeinsame Teiler von Zähler und Nenner des Bruches
rechts ≤ 4 (denn diese sind teilerfremd bis auf eine Zweierpotenz). Also folgt
tatsächlich
H(x1 ) ≥ 41 (a2 + b2 )2 ≥
1
4
max{|a|, |b|}4 > max{|a|, |b|} = H(x0 )
und H(x0 ) ≥ 2 (da x0 6= 0, ±1). Damit ist Satz 7 bewiesen. •
Man vergleiche diesen Beweis mit Fermats Originalbeweis (siehe [9] bzw. §IV.1
in [4]). Das obige Argument benutzt interessante Konzepte, die eine tragende Rolle in der Theorie elliptischer Kurven spielen: Die Höhe wird sich u.a.
im Beweis des Mordellschen Satzes als wichtig erweisen; ebenso die Gruppenstruktur, die sich insbesondere im Satz 8 wiederspiegelt. Diese Ideen lassen
sich auf gewisse ähnliche elliptische Kurven Y 2 = X 3 − n2 X ausdehnen, doch
dies ist ein Thema, welches wir in §10 besprechen werden.
7. Der Satz von Mordell
Nun wollen wir den Mordellschen Satz 4 aus §3 beweisen. Wir erinnern
seine Aussage: Die Gruppe der rationalen Punkte einer über Q definierten
elliptischen Kurve ist endlich erzeugt, d.h.
E(Q) ≃ Zr × T,
wobei r = rg(E) der Rang von E(Q) und T = Etors (Q) die Torsionsgruppe aller Elemente endlicher Ordnung ist. Wir beschränken uns aber auf den
42
ELLIPTISCHE KURVEN
Spezialfall
E : Y 2 = X 3 + aX + b = (X − θ1 )(X − θ2 )(X − θ3 )
mit ganzzahligen Wurzeln θj . Im Beweis werden uns tatsächlich viele alte Ideen
wieder begegegnen...¶
Y2 =X3 -62 X
20
P=H-3,9L
9360006 15120493920
P+Q=H €€€€€€€€€€€€€€€€€€€€€ , €€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€ L
1324801 1524845951
10
1074902978 394955797978664
Q=H- €€€€€€€€€€€€€€€€€€€€€€€€€€€€€ , €€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€€€ L
2015740609 90500706122273
-5
5
15
10
-10
-20
Abbildung 20. Die elliptische Kurve Y 2 = X 3 − 62 X mit etlichen
rationalen Punkten.
Seien zunächst zwei Punkte Pj = (xj , yj ) ∈ E(Q) mit x1 6= x2 gegeben.
Die Sekante durch P1 und P2 wird dann beschrieben durch
y2 − y1
Y = mX + c
mit m =
, c = y1 − mx1
x2 − x1
und P3 = P1 ∗ P2 sei der dritte Schnittpunkt mit E(Q). Wir führen neue
Parameter ein und setzen xj = uj + θ. Die kubische Gleichung
(mX + c)2 = X 3 + aX + b
wird gelöst von den x-Koordinaten der Punkte (x, y) = (xj , yj ) für j = 1, 2, 3.
Setzen wir xj = θj +uj ein, so ergibt sich durch Einsetzen in die Schnittpunktgleichung von Kurve und Gerade (nach ein wenig Rechnerei)
u3 + (3θ − m2 )u2 + (3θ 2 + a − 2m2 θ − 2mc)u + |θ 3 + {z
aθ + }b −(mθ + c)2 = 0
=0
¶
Unser Beweis geht auf Andre Weil zurück. In der Darstellung folgen wir dem Buch
mit dem irreführenden Namen The Riemann hypothesis and Hilbert’s tenth problem von S.
Chowla, Gordon & Breach, 1965; jener schreibt dort übrigens, dieser Beweis wäre ”nothing
beyond the capacity or ability of a ten-year old”.
7. Der Satz von Mordell
43
für u = uj . Das Polynom links faktorisiert sich als (u − u1 )(u − u2 )(u − u3 ),
so dass ein Koeffizientenvergleich auf
u1 u2 u3 = (mθ + c)2
bzw.
(12)
1
x3 − θ =
(x1 − θ)(x2 − θ)
(y2 − y1 )θ + x2 y1 − x1 y2
x2 − x1
führt. Falls P1 = P2 findet man analog
2
2
x1 − a − 2θx1 − 2θ 2
(13)
x3 − θ =
.
2y1
2
Lemma 1. Zu O =
6 (x, y) ∈ E(Q) gibt es x, y, z ∈ Z mit
y
x
x = 2, y = 3,
z
z
wobei ggT(x, z) = ggT(y, z) = 1.
Beweis. Sei x = nℓ , y = m
n mit o.B.d.A. ggT(ℓ, m, n) = 1. Dass dies wirklich
keine Einschränkung ist, zeigt Einsetzen in die E definierende Gleichung:
ℓ3
ℓ
m2
=
+a +b
2
3
n
n
n
bzw.
ℓ3 = n(m2 − aℓn − bn2 )
Sei jetzt d := ggT(ℓ, n), sowie ℓ = dℓ′ und n = dn′ mit also ggT(ℓ′ , n′ ) = 1.
Dann folgt
d2 ℓ′3 = n′ (m2 − aℓn − bn2 )
und ggT(d, m2 − aℓn − bn2 ) = 1.
Somit ist n′ = d2 n′′ für eine ganze Zahl n′′ und obige Gleichung lässt sich
umschreiben zu
ℓ′3 = n′′ (m2 − aℓn − bn2 )
mit
ggT(ℓ′ , n′′ ) = 1.
Mit der Teilerfremdheit folgt n′′ = 1 bzw. n′ = d2 und es ergibt sich
dℓ′
ℓ′
m
=
und
y = 3,
d3
d2
d
jeweils in offensichtlich gekürzter Form. Das Lemma ist bewiesen. •
x=
Sei nun O =
6 P = (x, y) ∈ E(Q) mit eben x = zx2 , y = zy3 . Dann ist
y2
x
x
x
2
y = 6 =
− θ1
− θ2
− θ3 ,
z
z2
z2
z2
bzw.
y2 = (x − θ1 z2 )(x2 − (θ2 + θ3 )xz2 + θ2 θ3 z4 ).
Die Koeffizienten einer algebraischen Gleichung sind elementarsymmetrische
Funktionen der Wurzeln der Gleichung. In unserem Fall bedeutet dies
θ1 + θ2 + θ3 = 0,
θ1 θ2 θ3 = −b
und θ2 θ3 = θ12 + a.
44
ELLIPTISCHE KURVEN
Unter Berücksichtigung der E definierenden Gleichung ergibt sich daher
y2 = (x − θ1 z2 )(x2 + θ1 xz2 + (θ12 + a)z4 ).
(14)
Lemma 2. Für θ ∈ {θ1 , θ2 , θ3 } seien
P = x − θz2
und
Q = x2 + θxz2 + (θ 2 + a)z4
(also P Q = y2 nach (14)). Dann gilt
ggT(P, Q) | (3θ 2 + a).
Man beachte, dass alle θj und damit auch a ganzzahlig sind!
Beweis. Zunächst gilt
−P (x + 2θz2 ) + Q = −x2 + θxz2 − 2θxz2 + 2θ 2 z4 + x2 + θxz2 + (θ 2 + a)z4
= (3θ 2 + a)z4
bzw. (wiederum nach einiger Rechnerei)
P (θ 2 + a)x + (θ 2 + a)θz2 + 2θ 2 Q = (3θ 2 + a)x2 .
Mit dem vorangegangenen Lemma folgt ggT(x, z) = 1 und damit die Behauptung des Lemmas. •
Nun seien mit M := ggT(P, Q) die Zahlen P ′ , Q′ erklärt durch P = M P ′
und Q = M Q′ mit ggT(P ′ , Q′ ) = 1. Es folgt daher aus (14)
y 2
y
y2 = P Q = M 2 P ′ Q′
bzw.
P ′ Q′ =
mit
∈ Z.
M
M
Da P ′ , Q′ teilerfremd sind und ihr Produkt ein Quadrat ist, folgt
P ′ = p2 , Q′ = q2
(15)
für gewisse
p, q ∈ Z
(was man mit der Argumentation im Beweis des Fermatschen Satzes 7 in §6
vergleiche.).
Lemma 3. Ist O =
6 (x, y) ∈ E(Q), dann gilt
x − θ = µα2
für
θ = θj ,
wobei α ∈ Q und µ entstammt einer endlichen Teilmenge ZE ⊂ Z.
Beweis. Es gilt
x−θ =
x
x − θz2
P
−θ =
= 2 =M
2
z
z2
z
2
p
.
z
Mit M = µ und pz = α zeigt sich vermöge Lemma 2 nun, dass µ ein Teiler von
3θ 2 + a ist. Da letztere Zahl nur endlich viele Teiler besitzt, entstammt µ also
einer endlichen Teilmenge von Z. •
Zu jedem (x, y) ∈ E(Q) \ {O} assoziieren wir nun ein Tripel (µ1 , µ2 , µ3 )
gemäß
x − θi = µi α2i ,
so dass
ZE ∋ µi | (3θi2 + a), αi ∈ Q.
7. Der Satz von Mordell
45
Dann folgt mittels Gleichung (12) bzw. im Tangentialfall (13) sofort µ1 µ2 µ3 =
β 2 für ein β ∈ Q. Ist nun ferner der Punkt P1 assoziiert mit (µ1 , µ2 , µ3 ) und
der Punkt P2 assoziiert mit (µ′1 , µ′2 , µ′3 ), so ist P3 = P1 ∗ P2 assoziiert mit
(µ1 µ′1 , µ2 µ′2 , µ3 µ′3 ), denn eben mit (12) bzw. (13) gilt
x3 − θ j =
1
1
· = µj µ′j · ,
·=
(x1 − θj )(x2 − θj )
µj µ′j
wobei das Quadratsymbol hier für nicht notwendig gleiche rationale Quadrate steht. Im Falle P1 = P2 ist P3 = P1 ∗ P2 assoziiert mit (1, 1, 1).
Im Folgenden geben wir nun den Beweis des Mordellschen Satzes (frei von
jeglicher Gruppentheorie, allerdings unter der Annahme der Ganzzahligkeit
der Wurzeln θi ). Wir zeigen hierzu:
Es gibt endlich viele Punkte aus denen sich jeder Punkt
P ∈ E(Q) durch endlich viele Anwendungen der SekantenTangenten-Methode konstruieren lässt.
Seien A1 , . . . , Aw die endlich vielen Punkte, die mit allen (endlich vielen) möglichen Tripeln (µ1 , µ2 , µ3 ) mit µj | (3θj2 + a) assoziiert sind. Sei P = ( zx2 , zy3 ) 6= O
nun irgendein Punkt aus E(Q) \ {O} (hierbei benutzen wir implizit Lemma 1
für die Form der Koordinaten). Dann existiert ein Punkt Av , so dass Av und
P mit demselben Tripel assoziiert sind, was wir kurz wie folgt ausdrücken:
P ∼ Av .
Dann ist nach unseren obigen Überlegungen Q := P ∗Av assoziiert mit (1, 1, 1)
und nach Satz 8 (multiplication by 2-map) gibt es
x1 y1
P1 =
,
∈ E(Q)
mit P1 ∗ P1 = Q
z21 z31
(denn x − θj = (x − θj ) · = ). Die Tangente an P1 geht also durch Q. Wir
führen nun diese Konstruktion fort:
xn yn
P 7→ P1 7→ P2 7→ . . . 7→ Pn =
,
,
z2n z3n
wobei jeweils Pj+1 sich aus Pj durch Tangentenbildung ergibt, wie zuvor P1
aus P0 = P .
Als wesentliches Werkzeug betrachten wir dabei nun die Höhe, definiert
durch
xn H(Pn ) = H 2 := max{|xn |, |z2n |}
zn
(vgl. §6). Wir wollen zeigen:
bzw.
p
H(P1 ) ≤ c H(P ),
p
H(Pn ) ≤ c H(Pn−1 )
mit einer Konstanten c, die nur von E und A1 , . . . , Aw abhängt.
46
ELLIPTISCHE KURVEN
Hierzu nehmen wir nun an, dass
ℓ m
P ∼ Av =
,
und
n2 n3
Q = P ∗ Av =
ξ η
,
ζ2 ζ3
.
Dann folgt (mit ein wenig Rechnerei)
ξ
(ℓx + an2 z2 )(ℓz2 + n2 x) + 2bn4 z4 − 2mnyz
=
;
ζ2
(ℓz2 − n2 x)2
im Gegensatz zu (12) setzt man hier wiederum die elliptische Kurvengleichung
mit der Tangentengleichung Y = mX + c gleich, ersetzt aber die unbekannte
Steigung m mittels eines Koeffizientenvergleichs. Man findet unschwer
(ℓx + an2 z2 )(ℓz2 + n2 x) + 2bn4 z4 − 2mnyz = O(H(P )2 )
mit einer nur von E und den Punkten A1 , . . . , Aw abhängigen impliziten Konstanten. Ferner gilt mit der E definierenden Gleichung
y2 = x3 + axz2 + bz4 = O(H(P )3 )
sowie yz = O(H(P )2 ). Insgesamt folgt daher
|ξ| ≤ cH(P )2
mit einer absoluten nur von E abhängigen Konstanten c. Eine analoge Abschätzung
gilt für den Nenner ζ 2 der x-Koordinate von Q und es folgt daher
H(Q) = max{|ξ|, |ζ 2 |} ≤ cH(P )2 .
Jetzt betrachten wir P1 ∗ P1 = Q mittels (13) machen wir den Ansatz
q
für j = 1, 2, 3,
(16)
± ξ − θj ζ 2 = e1 + e2 θj + e3 θj2
und erhalten also
e1 =
ζ(x21 − az41 )
−ζx1 z21
−ζz41
, e2 =
, e3 =
.
2y1 z1
y1 z1
y1 z1
Wir können (16) als ein lineares Gleichungssystem mit drei Gleichungen in
drei Unbekannten e1 , e2 , e3 auffassen, welches mit Hilfe der Cramerschen Regel
explizit gelöst werden kann. Bezeichnet nämlich


1 θ1 θ12
∆ := det 1 θ2 θ22  ,
1 θ3 θ32
so gilt sicherlich ∆ 6= 0 (da die θj paarweise verschiede sind). Die Cramersche
Regel zeigt
p
∆ej ∈ Z
und
∆ej = O( H(Q)) = O(H(P )).
Ferner folgt
∆(2e1 − ae2 ) =
∆ζ 2
x ,
y1 z1 1
−∆e3 =
∆ζ 4
z ∈ Z
y1 z1 1
7. Der Satz von Mordell
47
und also teilt y1 die Zahl ∆ζ (da y1 und z1 teilerfremd sind nach Lemma 1)
und ferner eilt z1 die Größe ∆ζ (da x1 und z1 teilerfremd sind nach Lemma 1).
Ausserdem sind y1 und z1 teilerfremd, womit also y∆ζ
ganzzahlig ist und
1 z1
p
∆ζ 2
x1 = ∆(2e1 − ae2 ) = O( H(Q))
y1 z1
p
4
2
bzw.
p x1 = O( H(Q)) gilt. Mit einem analogen Argument gewinnt man z1 =
O( H(Q)). Also folgt
p
1
H(P1 ) = max{|x1 |, |z21 |} = O(H(Q) 4 ) = O( H(P )).
Per Induktion ergibt sich
bzw.
q p
1
1
H(P2 ) ≤ c c H(P ) = c1+ 2 H(P ) 4
r q
p
1
1
−n
H(Pn ) ≤ c c . . . c H(P ) = c1+ 2 + 4 +...H(P )2 ≤ 2c2
1
für alle hinreichend großen n (denn limm→∞ H m = 1 für alle positiven H).
Damit sind sowohl xn als auch zn beschränkt durch die Konstante 2c2 ; gleiches
gilt für yn , denn auf Grund der E definierenden Gleichung gilt y2n = x3n +
axn z3n + bz4n . Dieser Teil des Beweises ist eine natürliche, wenn auch im Detail
sehr technische Fortführung der ermatschen Abstiegsmethode!
Also gehört Pn zu einer endlichen Menge rationaler Punkte auf E, etwa
B1 , . . . , Bk jeweils von der Form
s u
mit s, t, u ∈ Z, H(Bj ) ≤ 2c2 .
Bj = 2 , 3
t t
Sei also etwa Pn = Bj , dann ist Qn−1 = Bj ∗ Bj und Pn−1 = Qn−1 ∗ Ai mit
Ai ∼ Pn−1 . Nun definieren wir Qn−2 = Pn−1 ∗ Pn−1 sowie Pn−2 = Qn−2 ∗
Ak mit Ak ∼ Pn−2 . Fortführung dieses Arguments liefert mit Sekanten- und
Tangentenbildung also einen ’Startpunkt’ P = P0 und der Mordellsche Satz 4
ist bewiesen. •
Eine genaue Analyse des Beweises (mit zahlentheoretischen und algebraischen
Methoden) liefert eine Schranke für den Rang einer elliptischen Kurve E =
E(Q), nämlich
rg(E) ≤ n1 + 2n2 − 1,
wobei n1 die Anzahl der Primzahlen ist, die genau eine der Zahlen θi − θj mit
i 6= j teilen und n2 die Anzahl der Primzahlen, welche alle Zahlen θ1 − θ2 , θ1 −
θ3 , θ2 − θ3 teilen. (Einen Beweis findet man etwa in [4].) Diese Abschätzung
ist erstaunlich gut; beispielsweise gilt für die elliptische Kurve E : Y 2 =
(X − 1)X(X + 1) die Abschätzung
rg(E) ≤ 1 + 2 · 0 − 1 = 0,
in Übereinstimmung mit Satz 7.
48
ELLIPTISCHE KURVEN
8. Torsion
Unser nächstes Ziel ist die Beschreibung der rationalen Punkte endlicher
Ordnung einer elliptischen Kurve bzw. – gruppentheoretisch formuliert – der
Torsionsuntergruppe
T := {P ∈ E(Q) : nP = O für ein n ∈ N},
wobei 0 · P = O sei. Tatsächlich betrachten wir den Fall elliptischer Kurven,
die in Weierstraßscher Normalform durch ganzzahlige Koeffizienten gegeben
sind und wollen den Satz 5 von Nagell-Lutz aus §3 beweisen: Sei E eine elliptische Kurve mit definierender Gleichung Y 2 = X 3 + aX + b mit ganzzahligen
Koeffizienten a und b. Ist dann P = (x, y) ∈ T = Etors (Q) ein Torsionspunkt,
so gilt x, y ∈ Z und
y | (4a3 + 27b2 ) = −∆
falls
y 6= 0.
Tatsächlich kann man Satz 5 sogar mit der verschärften Bedingung y 2 | ∆
beweisen, uns genügt hier jedoch diese schwächere Form.
Abbildung 21. Links: Trygve Nagell, ∗ 1895 - † 1988; norwegischer
Zahlentheoretiker, der sich hauptsächlich im schwedischen Uppsala diophantischen Gleichungen widmete. Rechts: Hypatia aus dem vierten Jahrhundert; die womöglich erste Frau in der Mathematik, welche von fanatischen Christen ermordet wurde. Leider habe ich kein Foto der französischen Mathematikerin Élisabeth Lutz, ∗ 1914 - † 2008, gefunden; sie war
eine Schülerin von André Weil und arbeitete zu elliptischen Kurven über
p-adischen Körpern.
8. Torsion
49
Dieser Satz erlaubt die effektive Berechnung der Torsionsuntergruppe. Wir
starten mit einem Beispiel:
E1 : Y 2 = X 3 − X;
in diesem Fall ist die Diskriminante ∆ = 4 und als Kandidaten von Torsionspunkten P = (x, y) mit y 6= 0 kommen nur solche in Frage, für die also
y ∈ {±1, ±2, ±4}
gilt. Damit ist es ein Leichtes, die Torsionsgruppe zu bestimmen:
T1 = {O, (0, 0), (−1, 0), (+1, 0)}.
Ohne Beweis geben wir für die allgemeinere Kurve
En : Y 2 = X 3 − n2 X
mit n ∈ N
deren Torsionsgruppe durch
Tn = {O, (0, 0), (−n, 0), (+n, 0)}
an; die Torsionspunkte sind also in diesen Fällen neben dem unendlich fernen
Punkt O stets genau die Punkte mit verschwindender y-Koordinate und die
Torsionsgruppe ist stets isomorph zur Kleinschen Vierergruppe. (Ein Beweis
hierfür findet sich in [4].)
Der Beweis des Satzes von Nagell-Lutz benutzt das Konzept der p-adischen
Zahlen, welche von Hensel 1893 als Parallelwelt zu den reellen Zahlen eingeführt wurde. Hierzu sei p eine feste Primzahl; auf Grund der eindeutigen
Primfaktorzerlegung in Q existieren zu jedem 0 6= α ∈ Q von null verschiedene, teilerfremde ganze Zahlen a, b, so dass
a
α = · pνp (α)
mit ab 6≡ 0 mod p,
b
wobei νp (α) der Exponent von p in der Primfaktorzerlegung von α ist, den wir
im Folgenden die Ordnung von α nennen und mit
ord(α) = νp (α)
notieren wollen. Tatsächlich definiert
−νp (α)
p
|α|p =
0
falls
falls
α 6= 0,
α = 0.
einen nicht-archimedischen Absolutbetrag auf Q und |α|p ist genau dann ’klein’,
wenn α durch eine ’große’ Potenz von p teilbar ist. Diese Brücke zwischen
Analysis bzw. Topologie einerseits und Zahlentheorie andererseits erlaubt tiefe Einblicke in die Arithmetik, wie wir kurz skizzieren wollen.
Der Satz von Ostrowski liefert zunächst eine Charakterisierung aller topologisch inäquivalenter Absolutbeträge auf Q: Jeder nicht-triviale Absolutbetrag
auf Q ist äquivalent zu genau einem p-adischen Absolutbetrag | . |p oder aber
äquivalent zum Standardabsolutbetrag. Vervollständigt man nun den Körper
50
ELLIPTISCHE KURVEN
der rationalen Zahlen der Cantorschen Methode folgend (mit dem Quotienten der konvergenten rationalen Cauchy-Folgen modulo den Nullfolgen), so
ergeben sich neben den reellen Zahlen bzgl. der p-adischen Absolutbeträge für
jede Primzahl p der so genannte Körper Qp der p-adischen Zahlen. Insgesamt
entsteht also folgendes Bild:
Q
Vervollständigung
−→
Q2 , Q3 , Q5 , . . .
and
R.
Hierbei sind die Vervollständigungen paarweise verschiedenen und also jeweils
gleichberechtigte Zahlenuniversen (von denen sich jedoch außerhalb der Zahlentheorie der Körper der reellen Zahlen durchgesetzt hat).
Das Lokal-Global-Prinzip ist nun die Idee, globale Informationen (das sind
solche über den globalen Körper Q) aus lokalen Informationen (der lokalen
Körper Qp ) zu gewinnen. Ein einfaches Beispiel, welches sich sofort aus der
eindeutigen Primfaktorzerlegung ergibt, ist etwa, dass eine rationale Zahl genau dann ein Quadrat in Q ist, wenn es ein Quadrat in allen Qp und auch
(wegen des Vorzeichens) in R ist.
Ein tieferliegendes Beispiel ist der berühmte Satz von Hasse-Minkowski,
welcher besagt, dass eine quadratische Form q über Q eine rationale Zahl α
genau dann darstellt, also q(x) = α für ein x mit insbesondere x 6= 0 für
α = 0, wenn q die Zahl α über allen Qp sowie R darstellt. Diese Äquivalenz
ist tatsächlich nützlich, da die Darstellbarkeit durch quadratische Formen über
den lokalen Körpern i.A. leichter zu entscheiden ist, als über dem globalen Q.
Eine weitere Anwendung des Lokal-Global-Prinzips stellt die Vermutung
von Birch & Swinnerton–Dyer bereits (die wir in §9 behandeln werden). Mehr
zu dem faszinierenden Thema der p-adischen Zahlen findet der geneigte Leser
in [9]. Jetzt kehren wir zum Beweis des Satzes 5 von Nagell-Lutz zurück, der
einige Ideen p-adischer Zahlen in sich trägt.
Zu einem Punkt P = (x, y) ∈ E(Q) \ {O} gibt es nach Lemma 1 aus §7
ganze Zahlen x, y, z mit
y
x
x = 2, y = 3,
z
z
wobei ggT(x, z) = ggT(y, z) = 1. Angenommen, p ist eine Primzahl, welche
den Nenner von x oder den Nenner von y teilt, so folgt unmittelbar aus der
obigen Darstellung, dass p dann sowohl den Nenner von x als auch den von y
teilt sowie
3ord(x) = 2ord(y).
Wir definieren nun für ν ∈ N die Menge
E(pν ) := {(x, y) ∈ E(Q) \ {O} : ord(x) ≤ −2ν, ord(y) ≤ −3ν} ∪ {O}.
Dann gilt offensichtlich
. . . ⊂ E(pν+1 ) ⊂ E(pν ) ⊂ . . . ⊂ E(p2 ) ⊂ E(p) ⊂ E(Q);
beispielsweise ist hier E(p) die Menge aller rationalen Punkte (x, y) mit mindestens dem Teiler p2 des Nenners von x und mindestens dem Teiler p3 des
8. Torsion
51
Nenners von y sowie dem unendlich fernen Punkt. Unser erstes Ziel ist zu
zeigen, dass ein Punkt endlicher Ordnung (also ein Element der Torsionsuntergruppe) in keiner Menge E(p) für beliebige Primzahlen p liegen kann, denn
dann sind offensichtlich x und y ganzzahlig. Der p-adische Hintergrund besteht
darin, dass mit wachsendem ν die Punkte (x, y) ∈ E(pν ) p-adisch wachsende
Koordinaten besitzen und sich also dem unendlich fernen Punkt O annähern.
Hierzu vollziehen wir einen Koordinatenwechsel: Vermöge der Substitution
t = xy , s = y1 schreibt sich die E definierende kubische Gleichung
y 2 = x3 + ax + b
um zu
s = t3 + ats2 + bs3 ;
die Abbildung x = st , y = 1s ist bijektiv für y, s 6= 0 und bildet O auf den
Punkt (0, 0) in der (t, s)-Ebene ab. Die Punkte in der (t, s)-Ebene entsprechen
also eineindeutig den Punkten in der (x, y)-Ebene ohne O und den Punkten
der Ordnung zwei (denn 2P = O ist äquivalent zu y = 0). Der Geraden
Abbildung 22. Die Kurve y 2 = x3 +x+2 (links) und s = t3 +ts2 +2s3
nach dem Koordinatenwechsel (rechts). Aus der Achsensymmetrie der elliptischen Kurve in Weierstrass Normalform wird dabei eine Punktsymmetrie bzgl. des Nullpunktes.
y = λx + µ
in der (x, y)-Ebene entspricht dabei die Gerade
λ
1
s=− t+ .
µ
µ
in der (t, s)-Ebene. Wir untersuchen zunächst die Schnittpunkte von solchen
Geraden mit E bzgl. E(pν ):
52
ELLIPTISCHE KURVEN
Lemma 4. Die Menge
Rp := {x ∈ Q : ord(x) ≥ 0}
ist ein Ring, wobei ord( . ) die Ordnung bzgl. einer Primzahl p sei. Ferner
besitzt Rp eine eindeutige Primzerlegung und die Einheiten sind alle x ∈ Q
mit ord(x) = 0.
Insbesondere gilt für x ∈ Rp , dass x einen Nenner besitzt, der nicht durch p
teilbar ist.
Beweis durch Nachrechnen: Mit x, y ∈ Rp sind auch x ± y, x · y ∈ Rp . Die
Aussage über die Primzerlegung ist trivial, denn p ist das einzige Primelement.
Die Aussage über die Einheiten ist trivial. •
Sei nun (x, y) ∈ E(pν ) \ {O}, dann ist (s.o.)
m
d
x = p−2(ν+i)
und
y = p−3(ν+i)
n
e
für ein i ∈ N0 mit nicht durch p teilbaren ganzen Zahlen d, e, m, n. Also folgt
x
me ν+i
1
e
t= =
p
und
s = = p3(ν+i) ,
y
nd
y
d
d.h. es ist genau dann (t, s) ∈ E(pν ), wenn t ∈ pν Rp und s ∈ p3ν Rp .
Lemma 5. Für jedes ν ∈ N ist E(pν ) eine Untergruppe von E(Q) und die
Abbildung
x
ϕ : E(pν )/E(p3ν ) → pν Rp /p3ν Rp , P = (x, y) 7→ t(P ) = t = , O 7→ 0
y
ist ein Isomorphismus.
Beweis. Seien gegeben zwei verschiedene Punkte Pj = (tj , sj ) ∈ E(pν ). Angenommen t1 = t2 , so folgt über s1 6= s2 und damit y1 = −y2 sofort P1 = −P2
und P1 ⊕ P2 ∈ E(pν ). Der Fall t1 6= t2 ist schwieriger zu behandeln: Sei
s = αt + β die Gerade durch die Punkte P1 und P2 , so gilt
sj = t3j + atj s2j + bs3j
für j = 1, 2
und damit
s2 − s1 = t32 − t31 + a
(t2 s22 − t1 s21 )
|
{z
}
+b(s32 − s31 )
=(t2 −t1 )s22 +t1 (s22 −s21 )
Wegen t32 − t21 = (t2 − t1 )(t22 + t2 t1 + t21 ) folgt nach einiger Rechnerei für die
Steigung der Geraden durch P1 und P2
(17)
α=
t22 + t1 t2 + t21 + as22
s2 − s1
=
t2 − t1
1 − at1 (s2 + s1 ) − b(s22 + s1 s2 + s21 )
Auf Grund der 1 im Nenner dieses Ausdrucks ist α eine Einheit in Rp . Im
Falle P1 = P2 entsteht aus (17) durch Grenzübergang t2 → t1 , s2 → s1 die
Formel
3t21 + as21
.
α=
1 − 2at1 s1 − 3bs21
8. Torsion
53
Sei nun P3 = (t3 , s3 ) der dritte Schnittpunkt der Geraden mit E(Q). Substitutieren wir s = αt + β, so entsteht
αt + β = t3 + at(αt + β)2 + b(αt + β)3
bzw.
0 = (1 + aα2 + bα3 )t3 + (2aαβ + 3bα2 β)t2
(18)
+(aβ 2 + 3bαβ 2 − α)t + bβ 3 − β
= (1 + aα2 + bα3 )(t − t1 )(t − t2 )(t − t3 )
und ein weiterer (und nicht letzter) Koeffizientenvergleich zeigt
(19)
t1 + t2 + t3 = −
2aαβ + 3bα2 β
.
1 + aα2 + bα3
Abbildung 23. Die Addition auf der Kurve s = t3 + ts2 + 2s3 nach
dem Koordinatenwechsel.
Wir addieren nun P1 ⊕ P2 ähnlich wie in der (x, y)-Ebene, bloß unter Ersetzung des unendlich fernen Punktes O durch den Ursprung (0, 0) (entsprechend unserer Substitution) wie folgt: Bezeichnet P1 ∗ P2 = (t3 , s3 ) den dritten
Schnittpunkt der Geraden durch P1 und P2 , so sei
P1 ⊕ P2 = (−t3 , −s3 ),
also der dritte Schnittpunkt der Geraden durch P1 ∗ P2 und (0, 0). (Dies liefert
tatsächlich einen Punkt auf der elliptischen Kurve, denn mit (t, s) ist auch
(−t, −s) ein Punkt auf E).
Zurück zu α, gegeben durch (17); für t1 , s1 , t2 , s2 ∈ pν Rp ist der Zähler von
α ein Element in p2ν Rp und ebenso
−at1 (s2 + s1 ) − b(s22 + s2 s1 + s21 ) ∈ p2ν Rp .
54
ELLIPTISCHE KURVEN
Insbesondere ist der Nenner von α also eine Einheit in Rp und somit α ∈
p2ν Rp . Mit s1 ∈ p3ν Rp und t1 ∈ p2ν Rp folgt daher
β = s1 − αt1 ∈ p3ν Rp ,
wobei β der konstante Term in der Geradengleichung s = αt+β ist. Mit Formel
(18) ergibt sich analog t1 + t2 + t3 ∈ p3ν Rp und ferner mit t1 , t2 ∈ pν Rp folgt
−t3 ∈ pν Rp . Liegen also die t-Koordinaten von P1 , P2 in pν Rp , so auch die tKoordinate von P1 ⊕ P2 . Selbiges gilt für P = (t, s) und −P = (−t, −s). Damit
ist E(pν ) abgeschlossen bzgl. der Addition und der Bildung des Inversen, also
eine Gruppe! Tatsächlich haben wir
P1 , P2 ∈ E(pν )
=⇒
t(P1 ) + t(P2 ) − t(P1 ⊕ P2 ) ∈ p3ν Rp
bzw.
(20)
t(P1 ⊕ P2 ) ≡ t(P1 ) + t(P2 ) mod p2 Rp
gezeigt (hier ist die Addition links die auf E, während rechts in Rp ⊂ Q addiert
wird). Nun ist die Abbildung
φ : E(pν ) → Q,
P 7→ t(P )
kein Gruppenhomomorphismus (da i.A. die Kongruenz (20) keine Gleichung
ist), wohl aber, wenn wir nach dem Kern austeilen:
Ker φ = {P ∈ E(pν ) : t(P ) ∈ p3ν Rp }.
Damit ist das Lemma bewiesen. •
Nun sind wir bereit für den
Beweis von Satz 5. Sei m die Ordnung von P 6= O, also m 6= 1, sowie p
irgendeine Primzahl. Wir wollen zeigen, dass P 6∈ E(p) gilt.
Angenommen, P ∈ E(p). Dann kann P nicht in allen Mengen E(pν ) bei
ν ∈ N bestehen (klar), also existiert eine natürliche Zahl ν mit
(21)
P ∈ E(P ν ) \ E(P ν+1 ).
Im Falle p ∤ m folgt aus (20)
t(mP ) ≡ mt(P ) mod p3ν Rp
bzw., wegen mP = O,
0 = t(O) ≡ mt(P ) mod p3ν Rp .
Da aber m nach Voraussetzung invertierbar ist (da teilerfremd mit p), ergibt
sich notwendigerweise
0 = t(P ) mod p3ν Rp
und damit P ∈ E(p3ν ), der gewünschte Widerspruch zu (21).
Falls p | m, wenn also m = pn für ein n ∈ N, so betrachten wir den Punkt
′
P = nP ; dieser besitzt die Ordnung p (klar). Mit der Gruppeneigenschaft ist
mit P auch P ′ ein Element von E(p). Nehmen wir nun ferner
P ′ ∈ E(P ν ) \ E(P ν+1 )
8. Torsion
55
für ein ν ∈ N in Analogie zu (21) an, so folgt ähnlich
0 = t(O) = t(pP ′ ) ≡ pt(P ′ ) mod p3ν Rp
bzw. (nach Kürzen des Faktors p)
t(P ′ ) ≡ 0 mod p3ν−1 Rp
und wiederum der gewünschte Widerspruch zu (21).
Wir haben bislang also gezeigt, dass P 6∈ E(p) für alle Primzahlen p gilt,
wonach E(p) also keine Punkte endlicher Ordnung enthält. Ist also P = (x, y)
ein Punkt endlicher Ordnung, so sind die Nenner von x und y durch keine
Primzahl teilbar, also ganzzahlig!
Es verbleibt zu zeigen, dass im Falle y 6= 0 die Diskriminante ∆ = −(4a3 +
27b2 ) ein Vielfaches von y ist. Die Diskriminante ∆ ist dabei die Diskriminante
des kubischen Polynoms
f (X) := X 3 + aX + b = (X − α1 )(X − α2 )(X − α3 )
und damit auch
∆ = −(4a3 + 27b2 ) = (α1 − α2 )2 (α1 − α3 )2 (α2 − α3 )2
(das ist aus der Algebra bekannt, kann aber auch durch Nachrechnen sofort
verifiziert werden). Ferner ist aus der Algebra bekannt, dass für ein Polynom
f ∈ Z[X] mit Leitkoeffizient 1 dessen Diskriminante im von f und dessen
Ableitung f ′ erzeugten Ideal im Polynomring Z[X] liegt. In unserem Fall kann
man leicht eine entsprechende Linearkombination mit
(22) ∆ = −(4a3 + 27b2 ) = (18aX − 27b)f (X) + (−6aX 2 + 9bX − 4a2 )f ′ (X)
direkt angeben (wenn es auch mal wieder auf Rechnerei hinausläuft). Nun ist
wegen y 6= 0 sicherlich 2P = (x, y) 6= O. Mit P ist auch 2P von endlicher
Ordnung, besitzt also nach dem bereits Gezeigten ganzzahlige Koordinaten
x, y. Die Verdopplungsformel (Spezialfall des Gruppengesetzes) liefert nun
′ 2
f (x)
f ′ (x)
2x + x =
mit
∈ Z.
2y
2y
Insbesondere ist y ein Teiler von f ′ (x) und nach (22) somit auch von
(18aX − 27b)f (x) + (−6aX 2 + 9bX − 4a2 )f ′ (x)
= (18aX − 27b)y 2 + (−6aX 2 + 9bX − 4a2 )f ′ (x) = ∆.
Damit ist der Satz 5 von Nagell-Lutz bewiesen. •
Tatsächlich kann man zeigen, dass die elliptische Kurve E, gegeben durch
die Gleichung Y 2 = X 3 + dX mit d ∈ Z von einer Form d 6= m4 k für irgendwelche m, k ∈ Z über Q die Torsionsgruppe isomorph zu
• Z/2Z × Z/2Z, falls −d ein Quadrat ist,
• Z/4Z, falls d = 4,
• Z/2Z, sonst,
56
ELLIPTISCHE KURVEN
ist. Der Beweis benutzt etwas tieferliegende Konzepte p-adischer Zahlen (nämlich
so genannte ganze p-adische Zahlen) und wir verweisen für den nicht ganz einfachen Beweis auf [4].
9. Die Vermutung von Birch & Swinnerton-Dyer
Wir starten mit einer über Z definierten elliptischen Kurve E in Weierstraß
Normalform. Arithmetisch interessant ist u.a. die Größe der Gruppe der rationalen Punkte auf E, z.B. ob der Rang positiv ist und also E(Q) unendlich ist
oder aber der Rang gleich null ist und nur endlich viele rationale Punkte existieren. Hierzu mag man die Hoffnung hegen, mit einem Lokal-Global-Prinzip
durch Studium der Kurve über lokalen Körpern Z/pZ zu einer Primzahl p,
globale Informationen über etwa den Rang von E(Q) zu sammeln. Nach Reduktion modulo einer Primzahl p > 2 (welche die Diskriminante nicht teilt,
um eine glatte elliptische Kurve zu haben) sind dabei also die Lösungen der
Kongruenz
Y 2 ≡ X 3 + aX + b mod p
zu untersuchen. Für die Anzahl ♯E mod p dieser Lösungen modulo p wissen
wir mit dem Satz 6 von Hasse
√
(23)
|p + 1 − ♯E mod p| < 2 p.
In einem gewissen Sinne ist also p+1 der Erwartungswert für die Gruppenordnung ♯E mod p der reduzierten Kurve. Nun bilden wir (in gewisser Analogie
zum Problem der Primzahlverteilung in der Zahlentheorie) das Produkt
πE (x) :=
Y ♯E mod p
.
p
p≤x
Hier ist ein Faktor groß, wenn die elliptische Kurve bei Reduktion modulo
der entsprechenden Primzahl p viele Punkte enthält, also ♯E mod p größer als
der Erwartungswert p + 1 ausfällt. Nun mag man hoffen, dass viele Punkte
bei Reduktion modulo vieler Primzahlen sich zu vielen rationalen Punkten
zusammenfügen lassen! (Die Umkehrung gilt trivialerweise.) In eben diesem
Sinne vermuteten Birch & Swinnerton-Dyerk (auf der Basis von numerischem
Material):
Vermutung von Birch & Swinnerton–Dyer (1963/65). Ist E eine über
Z definierte elliptische Kurve, so gilt
Y ♯E mod p
∼ CE (log x)rg(E)
πE (x) =
p
p≤x
mit einer nur von E abhängigen Konstanten CE 6= 0 bei x → ∞.
k
B. Birch, H.P.F. Swinnerton–Dyer, Notes on elliptic curves, I+II, Journal für reine
und angewandte Mathematik 212 (1963), 7-25; 218 (1965), 79-108
9. Die Vermutung von Birch & Swinnerton-Dyer
57
Das Symbol ’∼’ bedeutet hierbei, dass der Quotient beider Seiten für gegen
unendlich wachsendes x sich immer mehr dem Wert eins annähert, also gewissermaßen beide Ingredienzen von derselben Größenordnung sind. Ist also
die Gruppenordnung ♯E mod p bei Reduktion für viele Primzahlen signifikant
größer als der Erwartungswert, so sollte πE (x) bei x → ∞ groß ausfallen, was
nur der Fall sein kann, wenn der Rang rg(E) der Kurve positiv ist. Dies ist
die so genannte schwache Form der Vermutung von Birch & Swinnerton-Dyer;
eine stärkere Form dieser Vermutung beinhaltet eine genaue Beschreibung der
Konstanten CE , in die weitere Strukturgrößen der elliptischen Kurve E eingehen. Diese Vermutung ist eines der sieben Millenniumsprobleme! Bislang
kennt man nur Teillösungen, die allerdings bereits beachtliche Konsequenzen
für die Mathematik liefern.
Nun wollen wir die Vermutung von Birch & Swinnerton-Dyer in eine analytische Gestalt bringen (wobei rudimentäre Vorkenntnisse in Funktionentheorie
und/oder analytischer Zahlentheorie ganz hilfreich sind). Bei der Frage der
Verteilung der Primzahlen studiert man die Riemannsche Zetafunktion
ζ(s) =
∞
X
Y
n−s
(1 − p−s )−1 =
p
n=1
als eine Funktion einer komplexen Veränderlichen s = σ + it; die Identität
zwischen dem so genannten Euler-Produkt links, das über alle Primzahlen erhoben ist, und der so genannten Dirichlet-Reihe rechts, ist eine analytische
Version der eindeutigen Primfaktorzerlegung der ganzen Zahlen (und beweist
sich leicht mittels der geometrischen Reihe). Diese Objekte konvergieren in der
Halbebene σ > 1 absolut und gleichmäßig auf jeder kompakten Teilmenge. Aus
der Existenz der Singularität in s = 1 (wenn die Dirichlet-Reihe zur divergenten harmonischen Reihe wird) folgt bereits die Unendlichkeit der Menge der
58
ELLIPTISCHE KURVEN
Primzahlen (ansonsten wäre ja das Produkt für s = 1 konvergent) und mit
mehr funktionentheoretischem Werkzeug sogar der Primzahlsatz
x
♯{p ≤ x : p prim} ∼
bei x → ∞.
log x
In diesem Zusammenhang sei mit der Riemannschen Vermutung ein anderes
Millennium-Problem erwähnt: Liegen alle nicht-reellen Nullstellen von ζ(s)
auf der so genannten kritischen Geraden s = 12 + iR? Ein Nachweis hiervon
würde eine erheblich bessere Abschätzung des Fehlerterms im Primzahlsatz
liefern. Tatsächlich besteht ein enger Zusammenhang zwischen der Lage der
Nullstellen von ζ(s) und der Verteilung der Primzahlen.
In Analogie zur Riemannschen Zetafunktion definieren wir – Hasse folgend
– die zu einer elliptischen Kurve assoziierte L-Funktion durch
Y
Y
(24)
L(s; E) =
(1 − ap p−s )−1 (1 − ap p−s + p1−2s )−1 ,
p∤∆
p|∆
wobei
ap := p + 1 − ♯E mod p
und ∆ die Diskriminante ist; dabei gibt es natürlich nur endlich viele Primteiler
p | ∆. Bekanntlich konvergiert ein Euler-Produkt genau dann absolut und
gleichmäßig,
Y
(1 − ap p−s ) < ∞,
p
wenn
X
p
log |1 − ap p−s | < ∞
bzw.
X
p
|ap |p−σ < ∞
(hier haben wir im Wesentlichen Beträge gesetzt, den Logarithmus und anschließend die Taylorentwicklung angewandt). Im Falle der L-Funktion einer
elliptischen Kurve liefert Hasses Abschätzung (23) daher die Konvergenz für
σ > 32 .
Vergessen wir zunächst unsere gute Schule (sprich: Vorsicht bei Konvergenz) und nehmen an, das L(s; E)-definierende Produkt sei konvergent für s =
1, dann ließe sich das Produkt aus der Birch & Swinnerton-Dyer-Vermutung
aus einem Wert der L-Funktion ablesen: Lassen wir die Teilerbedingung für
die Primzahlen außer acht, gilt nämlich
Y
p
≈ lim πE (x)−1 .
L(1; E) ≈
x→∞
♯E
mod
p
p
Unglücklicherweise ist das Euler-Produkt links der absoluten Konvergenzhalbebene nicht konvergent und somit der Wert L(1; E) zunächst ohne weiteren Sinn. Hasse vermutete, dass L(s; E) in die ganze komplexe Ebene analytisch fortsetzbar ist (wenn auch leider nicht durch obiges Produkt) und einer bestimmten Funktionalgleichung genügt (ähnlich der der Zetafunktion;
siehe (25) weiter unten). Damit lässt sich nun die Vermutung von Birch &
Swinnerton–Dyer auch über die zu einer elliptischen Kurve E assoziierten LFunktion erklären, nämlich:
9. Die Vermutung von Birch & Swinnerton-Dyer
59
Analytische Version der Vermutung von Birch & Swinnerton–Dyer.
Ist E eine über Z definierte elliptische Kurve, so gilt
rg(E) > 0
⇐⇒
L(1; E) = 0.
Eine genauere Version dieser Vermutung besagt, dass die Ordnung der Nullstelle von L(s; E) in s = 1 (im funktionentheoretischen Sinne) genau mit
dem Rang der elliptischen Kurve übereinstimmt – ein interessantes Wechselspiel zwischen Analysis und Arithmetik! Ist die Vermutung von Birch &
Swinnerton-Dyer richtig, so liefert sie letztlich einen Algorithmus, der erlaubt
sämtliche rationalen Punkte einer elliptischen Kurve zu bestimmen.
Jetzt wollen wir die Frage untersuchen, was genau Hasse auf diese Form
L(s; E) einer erzeugenden Funktion gebaut aus den lokalen Daten der elliptischen Kurve geführt hat. Gegeben eine Primzahl p erklären wir die lokale
Zetafunktion durch
!
∞
X
♯E(Fpn ) n
u .
Z(u; Ep ) := exp
n
n=1
Tatsächlich zeigte Hasse über Satz 6 hinaus
♯E(Fpn ) = pn + 1 − (αn + β n ),
wobei X 2 − ap X + p = (X − α)(X − β) mit zwei komplexen Wurzeln α, β.
Damit determiniert der Fall der Reduktion modulo p (wenn also n = 1) den
Rest (d.h. n ≥ 2) und es berechnet sich nun
∞
X
1
(pu)n + un − (αu)n − (βu)n .
log Z(u; Ep ) =
n
n=1
Mit Hilfe der Taylorentwicklung des Logarithmus,
− log(1 − z) =
folgt daher
Z(u; Ep ) =
∞
X
zn
n=1
n
,
1 − ap u + pu2
(1 − αu)(1 − βu)
=
,
(1 − u)(1 − pu)
(1 − u)(1 − pu)
Die lokale Zetafunktion ist somit eine rationale Funktion. Die Nullstellen des
Zählers berechnen sich damit als Paar komplex konjugierter Nullstellen
q
1
1
mit |uk |2 = u1 u2 =
u1,2 = (ap ± a2p − 4p)
2p
p
1
und also |u1 | = |u2 | = p− 2 (innerhalb des Konvergenzbereiches der obigen
Reihenentwicklung). Setzen wir nun u = p−s , so liegen die Nullstellen von
Z(p−s ; Ep ) auf der kritischen Geraden Re s = 21 und unsere lokale Zetafunktion erfüllt das Analogon der Riemannschen Vermutung für die Riemannsche
Zetafunktion. Entsprechend nennt man den Satz von Hasse auch die ’Riemannsche Vermutung für Kurven’ und dies wird oft auch als Indiz für die Richtigkeit
60
ELLIPTISCHE KURVEN
der klassischen Riemannschen Vermutung ins Spiel gebracht.∗∗ Der Realteil der
kritischen Geraden entspricht dabei genau dem Exponenten in Hasses Relation
(23).
Es gibt eine weitere Analogie: Für ζ(s) besteht bekanntlich die Funktionalgleichung
s
π − 2 Γ( 2s )ζ(s) = π −
(25)
1−s
2
Γ( 1−s
2 )ζ(1 − s).
Ganz ähnlich besitzt auch unsere lokale Zetafunktion eine Funktionalgleichung: Es gilt nämlich
Z(p−s ; Ep ) =
=
1 − Ap−s + p1−2s
(1 − p−s )(1 − p1−s )
p1−2s 1 − Aps−1 + p2s−1
= Z(ps−1 ; Ep );
p1−2s (1 − ps−1 )(1 − ps )
dies ist wie bei der Riemannschen Zetafunktion eine Punktsymmetrie s ↔
1 − s und die Nullstellen von Z(p−s ; E) liegen also auf der Symmetrieachse
dieser Funktionalgleichung. Nun erklären wir die globale Zetafunktion einer
elliptischen Kurve E formal durch das Euler-Produkt
Y
Z(s; E) :=
Z(p−s ; Ep ),
p
wobei wir für Primteiler p der Diskriminante
Z(p−s ; Ep ) = (1 − p−s )−1 (1 − p1−s )−1
setzen (diese Faktoren enthalten keine Informationen über E, erweisen sich
aber weiter unten als recht natürlich). Damit gilt also
Y
Y
(1 − ap p−s + p1−2s ).
Z(s; E) =
(1 − p−s )−1 (1 − p1−s )−1
p
p∤∆
Dieser Ausdruck ist annähernd
Y
Y
Y
(1 − ap p−s ) (1 − ap p−s + p1−2s )
≈
(1 − p−s )−1 (1 − p1−s )−1
p
p|∆
p∤∆
= ζ(s)ζ(s − 1)L(s; E)−1
mit der Hasse L-Funktion L(s; E), definiert in (24). Hasse vermutete für
L(s; E)
• eine analytische Fortsetzung in die ganze komplexe Ebene,
• eine Funktionalgleichung (mit einer Symmetrie s ↔ 2 − s):
√ !2−s
√ !s
N
N
Γ(s)L(s; E) = ω
Γ(2 − s)L(2 − s; E)
2π
2π
mit einem Vorzeichen ω = ±1 und einer natürlichen Zahl N .
∗∗
Weitreichende Verallgemeinerungen gehen zurück auf Weil und Deligne und ihre Beweise sind keineswegs trivial. Da jedoch ζ(s) eine transzendente Funktion ist, sollte die
ursprüngliche Riemannsche Vermutung viel schwieriger zu beweisen sein...
9. Die Vermutung von Birch & Swinnerton-Dyer
61
Ist übrigens das Vorzeichen negativ, so folgt unmittelbar L(1; E) = 0 und
unter der weiteren Annahme der analytischen Form der Birch & Swinnerton–
Dyer-Vermutung somit ein positiver Rang der elliptischen Kurve E(Q), bzw.
die Existenz unendlich vieler rationaler Punkte.
Wir blicken nun kurz auf einen Beweis der Funktionalgleichung für die
Riemannsche Zetafunktion, und zwar einen der beiden, die Riemann selbst
gab: Für σ > 1 findet man durch eine geeignete Substitution im definierenden
Integral der Gammafunktion
Z ∞
s
− 2s
−s
s
π Γ( 2 )n =
x 2 −1 exp(−πn2 x) dx
0
und nach Summation über alle natürlichen Zahlen n
Z ∞
∞
∞
X
X
s
s
exp(−πn2 x) dx;
x 2 −1
n−s =
(26)
π − 2 Γ( 2s )
n=1
0
n=1
hier ist die Reihe links die ζ-definierende Dirichlet-Reihe, während rechts die
’halbe’ Thetafunktion
∞
X
exp(πin2 τ )
ϑ(τ ) =
n=−∞
vermindert um den konstanten Term auftritt. Aus dieser Integraldarstellung
gewinnt man nun leicht die analytische Fortsetzung von ζ(s) nach C \ {1} und
die Funktionalgleichung (25). Hierzu benutzt man die Modularitätseigenschaft
der Thetafunktion, insbesondere die Transformationsformel
q
ϑ(− τ1 ) = τi ϑ(τ )
für komplexe τ der oberen Halbebene, welches die Invarianz des Integrals in
(26) bzgl. der Transformation s 7→ 1 − s impliziert. Es sind nicht viele Methoden zur analytischen Fortsetzung von Dirichlet-Reihen bekannt und tatsächlich
kann man auch Beispiele konstruieren, die sich nicht über eine gewisse Barriere hinweg fortsetzen lassen. Für die wichtige Klasse der Dirichlet-Reihen
zu Modulformen gelang jedoch Hecke 1936 der Nachweis einer tiefliegenden
Korrespondenz:
Dirichlet-Reihen mit
Funktionalgleichung
⇐⇒
Modulformen der
oberen Halbebene
Hierbei sind Modulformen definiert als holomorphe Funktionen f der oberen
Halbebene H := {τ = x + iy : y > 0}, welche den folgenden Eigenschaften
genügen.
• Funktionalgleichungen: Für alle τ ∈ H gilt
a b
aτ + b
k
= (cτ + d) f (τ )
für alle
∈ SL2 (Z);
f
cτ + d
c d
• Regularitätsbedingung: Die Abbildung τ := x + iy 7→ y k |f (τ )|2 ist
beschränkt auf H.
62
ELLIPTISCHE KURVEN
Hierbei heißt k das Gewicht (und ist zunächst eine gerade natürliche Zahl). Oft
ist es auch sinnvoll, Modulformen zu Untergruppen der SL2 (Z) zu definieren,
etwa zur Kongruenzuntergruppe
a b
Γ0 (N ) :=
∈ SL2 (Z) : c ≡ 0 mod N
c d
zur Stufe N . Wegen ( 10 11 ) ∈ Γ0 (N ) besitzen solche Modulformen für τ ∈ H
insbesondere eine Fourier-Reihenentwicklung
∞
X
c(n) exp(2πinτ )
f (τ ) =
n=1
mit gewissen komplexen Koeffizienten c(n). Hecke folgend lässt sich zu einer
solchen Modulform f eine L-Funktion vermöge
∞
X
c(n)
L(s; f ) =
ns
n=1
assoziieren. Unter gewissen Umständen sind die Fourier-Koeffizienten c(n)
multiplikativ, so dass dann die definierende Dirichlet-Reihe in Analogie zu
zeta eine Darstellung als Euler-Produkt besitzt:
−1
Y
c(p) −1 Y
c(p)
1
L(s; f ) =
1− s
1 − s + 2s+1−k
.
p
p
p
p|N
p∤N
Ferner verifizierten Hecke bzw. Atkin & Lehner das Bestehen einer Funktionalgleichung der Form
s
N 2 (2π)−s Γ(s)L(s, f ) = ±N
k−s
2
(2π)s−k Γ(k − s)L(k − s, f ).
In den 1960er Jahren formulierten die japanischen Mathematiker Shimura & Taniyama einen erstaunlichen Zusammenhang zwischen prinzipiell verschiedenen L-Funktionen: Demnach sollte es zu über Q definierten elliptischen
Kurve E eine Modulform f vom Gewicht k = 2 zu einer bestimmten Stufe N
geben, so dass die assoziierten L-Funktionen übereinstimmen:
L(s; E) = L(s; f );
insbesondere stimmen damit auch die Koeffizienten in den Reihenentwicklungen überein (auf Grund des Identitätssatzes für Dirichlet-Reihen), was wichtige arithmetische Informationen über die elliptische Kurve via den analytischen Modulformen liefert. Diese erstaunliche Brücke zwischen elliptischen
Kurven einerseits und Modulformen andererseits wurde schließlich durch den
Beweis der Shimura-Taniyama-Vermutung von Wiles et al. sicher gestellt (wobei auch sein Beweis der Fermatschen Vermutung abfiel; siehe §6). Kurz: elliptische Kurven sind modular! Insbesondere wurden so die Vermutungen Hasses über die analytische Fortsetzbarkeit und die Funktionalgleichung von LFunktionen zu elliptischen Kurven verifiziert. Speziell für die elliptische Kurve
E : Y 2 = X 3 − X ergeben sich so die L-Funktion
L(s; E) = (1 + 31−2s )−1 · (1 + 2 · 5−s + 51−2s )−1 · . . .
10. Das Kongruenzzahlproblem
63
und die Modulform
f (τ ) = q − 2q 5 − 3q 9 + . . .
mit
q = exp(2πiτ ),
welche Gewicht k = 2 und Stufe N = 32 besitzt. Dieser und weitere Spezialfälle
wurden vor Wiles von Eichler, Shimura und Tunnell bewiesen. Eine wichtige
ungelöste Frage in diesem Kontext: Falls eine Euler-Produktdarstellung für
L(s; E) (bzw. L(s; f )) besteht, gilt dann ein Analogon der Riemannschen Vermutung, wie es für ζ(s) angenommen wird?
Was ist bekannt hinsichtlich der Vermutung von Birch & Swinnerton–Dyer?
Beispielsweise zeigte Kolyvagin 1989, dass ein Nichtverschwinden von L(s; E)
für s = 1 nach sich zieht, dass der Rang der Kurve null ist; ferner zeigte er,
dass eine einfache Nullstelle in s = 1 (also L(1; E) = 0 6= L′ (1; E)) den Rang
eins impliziert. Für spezielle elliptische Kurven (mit komplexer Multiplikation)
sind weitere Ergebnisse bekannt, u.a. von Coates & Wiles sowie Gross & Zagier
und einigen weiteren. Eine vollständige Lösung der Vermutung von Birch &
Swinnerton-Dyer scheint jedoch noch in weiter Ferne zu liegen.
10. Das Kongruenzzahlproblem
Eine natürliche Zahl n heißt Kongruenzzahl, falls es ein rechtwinkliges
Dreieck mit rationalen Seitenlängen und Flächeninhalt n gibt, wenn also mit
Blick auf den Satz des Pythagoras a, b, c ∈ Q existieren, so dass
(27)
a2 + b2 = c2
und
n = 12 ab.
Diese Fragestellung ist ca. eintausend Jahre alt und wurde von arabischen
Mathematikern gestellt. Mit Euklids Parametrisierung der pythagoräischen
Tripel (Satz 1) findet man bereits unendlich viele Beispiele für Kongruenzzahlen: Z.B. liefert das Tripel 3, 4, 5 ein rechtwinkliges Dreieck mit Flächeninhalt
6 und sogar ganzzahligen Seitenlängen. Ein weiteres Beispiel ist n = 5, wie
bereits Fibonacci wusste und wir leicht der Gleichung
2 2 2
20
41
3
+
=
2
3
6
entnehmen. Viel schwieriger ist es aber, wenn man für eine gegebene Zahl
entscheiden soll, ob diese eine Kongruenzzahl ist oder nicht. Dies ist das so genannte Kongruenzzahlproblem. Alle Kongruenzzahlen ergeben sich letztendlich aus pythagoräischen Tripeln, allerdings liegt eine tückische Schwierigkeit darin, dass nicht nur ganzzahlige sondern allgemeiner rationale Seitenlängen zugelassen sind!
Um dieses Problem nicht zu unterschätzen, fragen wir ganz explizit: Ist 1
eine Kongruenzzahl oder aber 157? Das Dreieck in Abbildung 24 verifiziert
sofort, dass letztere 157 tatsächlich eine Kongruenzzahl ist. Doch wie findet
man ein solches Dreieck? Ein anderes Problem ist es, auszuschließen, dass eine
gegebene Zahl n keine Kongruenzzahl ist, es also kein Dreieck mit rationalen
64
ELLIPTISCHE KURVEN
224403517704336969924557513090674863160948472041
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€
8912332268928859588025535178967163570016480830
411340519227716149383203
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
21666555693714761309610
157
6803298487826435051217540
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€
411340519227716149383203
Abbildung 24. Ein rechtwinkliges Dreieck mit rationalen Seitenlängen und Fläche 157. Dieses Dreieck ist das kleinst mögliche in dem
Sinne, dass die Nenner und Zähler der Seitenlängen minimal sind mit dieser
Eigenschaft. (Das Beispiel wird Don Zagier zugeschrieben.)
Seiten und Fläche n gibt. Die Zahl 1 ist beispielsweise von diesem Typ, wie bereits Fermat mit seinem Verfahren des unendlichen Abstieges beweisen konnte
(was wir weiter unten in einer anderen Form reproduzieren wollen). Glücklicherweise für die Mathematik hat er für dieses Mysterium, wie Weil äußerte,
genügend Platz gefunden, um es irgendwo am Rande niederzuschreiben.
Zunächst gilt es jedoch, das Kongruenzzahlproblem in die Theorie elliptischer Kurven zu übersetzen. Hierzu zeigen wir
Lemma 6. Eine natürliche Zahl n ist genau dann eine Kongruenzzahl, wenn
es drei Quadrate rationaler Zahlen in arithmetischer Progression und gemeinsamer Differenz n gibt, d.h. es existieren x, y, z ∈ Q mit
(28)
y2 = x2 − n
und
z2 = x2 + n.
Beweis. Angenommen, (27) gilt, so folgt wegen b =
c 2 a 2 n 2
=
+
2
2
a
2n
a
bzw.
c 2
n 2
±n=
;
±
2
2 a
damit sind die drei Quadrate in arithmetischer Progression gefunden. Umgekehrt gilt mit (28)
a
2n = z2 − x2 + x2 − y2 = z2 − y2
bzw. n = 12 (z − y)(z + y). Damit zeigt sich
(z + y)2 + (z − y)2 = 2(z2 + y2 ) = (2x)2 .
Also gilt auch die Umkehrung. •
10. Das Kongruenzzahlproblem
65
Der Beweis ist konstruktiv! Beispielsweise übersetzt sich das pythagoräische
Tripel 3, 4, 5 in die drei Quadrate
2
2
2
1
5
7
1
25
49
= ,
= ,
=
2
4
2
4
2
4
mit gemeinsamer Differenz 6.
Projektiv beschreibt (28) den Schnitt zweier Quadriken und definiert damit eine Raumkurve vom Grad vier, was projiziert in die Ebene eine glatte
kubische Kurve liefert:
Satz 9. Eine natürliche Zahl n ist genau dann eine Kongruenzzahl, wenn die
elliptische Kurve
En : Y 2 = X 3 − n2 X
einen rationalen Punkt (x, y) mit y 6= 0 besitzt bzw. der Rang von En positiv
ist.
Im Hinblick auf unsere Untersuchungen aus §8 im Umfeld des Satzes 5 von
Nagell-Lutz sind die Punkte endlicher Ordnung von En gegeben durch O,
(0, 0), (−n, 0) und (n, 0), weshalb sich das Kriterium des Satzes auch durch
den Rang von En ausdrücken lässt.
Beweis. Angenommen, n ist eine Kongruenzzahl, so liefert das vorangegangene Lemma die Existenz einer arithemtischen Progression rationaler Quadrate
mit gemeinsamer Differenz n. Mit der obigen Schreibweise folgt daher durch
Multiplikation derselben
(xyz)2 = (x2 − n)x2 (x2 + n).
Setzen wir nun y = xyz und x = x2 , so folgt
y 2 = (x − n)x(x + n) = x3 − n2 x
und damit ist ein Punkt (x, y) auf En (Q) gefunden. Aus y = 0 folgt sofort
x = 0 oder x = ±n, was xyz = 0 impliziert und kein Dreieck liefert.
Definieren umgekehrt die rationalen Zahlen a, b, c ein rechtwinkliges Dreieck
mit Fläche n, so seien
x=
a(a − c)
2
und
y=
a2 (a − c)
.
2
Dann ist y 6= 0 (wegen a 6= c) und durch Nachrechnen verifiziert sich leicht
(x, y) ∈ En (Q), was wir dem geneigten Leser überlassen wollen. •
Es ist erstaunlich, dass sich das gut eintausend Jahre alte Kongruenzzahlproblem äquivalent in die Sprache der elliptischen Kurven übersetzen lässt.
Diese Theorie ermöglicht nun sofort tiefere Einblicke: Zunächst einmal ist die
Korrespondenz zwischen rechtwinkligen Dreiecken mit rationalen Seitenlängen
66
ELLIPTISCHE KURVEN
a, b, c und Flächeninhalt n und Punkten (x, y) unendlicher Ordnung auf der
elliptischen Kurve En (Q) explizit (wenngleich auch nicht eindeutig):
a(a − c) a2 (a − c)
(a, b, c) 7→
,
,
2
2
y 2nx n2 + x2
(x, y) 7→
,
,
,
x y
y
wobei die Seitenlängen natürlich immer mit einem positiven Vorzeichen auszustatten sind. Beispielsweise korrespondiert so Fibonaccis rechtwinkliges Dreieck zur Kongruenzzahl n = 5 (s.o.) mit dem rationalen Punkt (−4, 6) ∈ E5 .
Ferner folgt, dass bereits mit einem einzigen rechtwinkligen Dreieck mit rationalen Seiten und Fläche n automatisch unendlich viele solcher existieren, da
ein jedes dieser Art einem rationalen Punkt unendlicher Ordnung entspricht!
So liefert eine Punktverdopplung in Fibonaccis Beispiel
1681 62 279
,−
,
2(−4, 6) =
144
728
was auf das rechtwinklige Dreieck mit Seitenlängen
Flächeninhalt n = 5 führt. (Bitte Nachrechnen!)
1519 4920 334 4161
492 , 1519 , 747 348
Y2 =X3 -62 X
20
P=H-3,9L
9360006 15120493920
P+Q=H €€€€€€€€€€€€€€€€€€€€€ , €€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€ L
1324801 1524845951
10
1074902978 394955797978664
Q=H- €€€€€€€€€€€€€€€€€€€€€€€€€€€€€ , €€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
€€€€€€€€€€€ L
2015740609 90500706122273
-5
5
10
15
-10
-20
Abbildung 25. Die Addition gewisser Punkte auf der elliptischen Kurve Y 2 = X 3 − 62 X; den Punkten P und Q entsprechen die Dreiecke mit
Seitenlängen 3, 4, 5 bzw. 8518220204
, 3122541453 , 18428872963986767525 , jeweils
104084715 2129555051 2216541307731009701
mit Flächeninhalt 6. Jeder weitere rote Punkt steht für ein weiteres Vielfaches von (−3, 9) bzw. einem Dreieck mit Fläche 6.
und
10. Das Kongruenzzahlproblem
67
Korollar 1 (Fermat). Eine Quadratzahl ist nie eine Kongruenzzahl.
Beweis. Auf Grund der Homogenität der Polynome in a, b, c in (27) genügt
es die Quadratzahl 1 zu betrachten. Ist nämlich n = m2 eine Kongruenzzahl,
so folgte aus (27)
a2 + b2 = c2
und
2m2 = ab
für gewisse a, b, c ∈ Q. Nach Division durch m2 ergäbe sich dann aber ein
a b c
rechtwinkliges Dreieck mit Seitenlängen m
, m , m und Flächeninhalt 1. Dass
n = 1 aber keine Kongruenzzahl sein kann, folgt mit Hilfe von Satz 9 sofort
aus Satz 7, da E1 keine rationalen Punkte unendlicher Ordnung enthält. •
Die Verbindung zu elliptischen Kurven lässt hoffen, das Kongruenzzahlproblem durch die gut ausgebaute Theorie elliptischer Kurven zu lösen. Und
tatsächlich gelang Tunnell∗ ein bemerkenswertes Resultat in dieser Richtung.
Mit Hilfe elliptischer Kurven und der Theorie der Modulformen fand er einen
einfachen Algorithmus, der in endlicher Zeit entscheidet, ob eine gegebene Zahl
eine Kongruenzzahl ist oder nicht. Allerdings basiert dieser Algorithmus auf
der Richtigkeit der bislang ungelösten Vermutung von Birch & SwinnertonDyer:
Satz von Tunnell. Ist n ∈ N quadratfrei, so gilt
Z
dx
a(N − 2M )2 ∞
√
√
,
L(1; En ) =
16 n
x3 − x
1
wobei a gleich eins oder zwei ist, je nachdem ob n ungerade oder gerade ist,
und N für die Anzahl der ganzzahligen Lösungen der quadratischen Gleichung
2X 2 + Y 2 + 8Z 2 = na sowie M die Anzahl der ganzzahligen Lösungen der
quadratischen Gleichung 2X 2 + Y 2 + 32Z 2 = na steht.
Wir dürfen annehmen, dass n quadratfrei ist. Der Satz von Tunnell besagt,
dass für eine Kongruenzzahl n die Relation N = 2M für die Anzahl der Darstellungen von n durch gewisse quadratische Formen bestehen muss; ansonsten
wäre L(1; En ) 6= 0 nach einem oben erwähnten Resultat von Coates & Wiles
im Widerspruch zu dem positiven Rang von En (Q) nach Satz 9. Die Richtigkeit der Vermutung von Birch & Swinnerton-Dyer würde auch die Umkehrung
dieser Aussage erlauben: Wenn N = 2M gilt, so ist zunächst also L(1; En ) = 0
und damit der Rang von En (Q) positiv und also n eine Kongruenzzahl. Übrigens wäre damit jede Zahl n ≡ 5, 6 oder 7 mod 8 als Kongruenzzahl nachgewiesen. Da die involvierten quadratischen Formen positiv definit sind, und
das Kriterium sich auf ganzzahlige Darstellungen bezieht, kommen letztlich
nur endlich viele Tripel (x, y, z) überhaupt bei der Darstellbarkeit von n in
Frage. Der Tunnellsche Beweis ist leider nicht einfach, weshalb wir auf [6]
verweisen.
∗
J. Tunnell, A classical diophantine problem and modular forms of weight 3/2, Inventiones math. 72 (1983), 323-334.
68
ELLIPTISCHE KURVEN
Als Nächstes wollen wir Chahal† folgend eine unendliche Familie von Kongruenzzahlen angeben:
Satz 10 (Chahal, 2006). Für jedes m ∈ N ist n = m(4m2 + 1) eine Kongruenzzahl.
Beweis. Wir starten mit einer (wirklich) alten Identität von Desboves:‡
(Y 2 + 2X Y − X 2 )4 + (2X 3 Y + X 2 Y 2 )(2X + 2Y)4
= (X 4 + Y 4 + 10X 2 Y 2 + 4X Y 3 + 12X 3 Y)2 .
Mit der Substitution X = 1 − 2λ, Y = 4λ ergibt sich
(1 − 12λ + 4λ2 )4 + 8λ(2λ − 1)2 (2(1 + 2λ))4
= (1 + 40λ − 104λ2 + 160λ3 + 16λ4 )2
und es entsteht ein Punkt P = (x, y) mit den Koordinaten
(1 − 12λ + 4λ2 )2
,
4(1 + 2λ)2
(1 − 12λ + 4λ2 )(1 + 40λ − 104λ2 + 160λ3 + 16λ4 )
y = y(λ) =
8(1 + 2λ)3
auf der elliptischen Kurve
x = x(λ) =
(29)
Y 2 = X 3 + dX
mit
d = d(λ) = 8λ(2λ − 1)2 .
Genügt nun n der Gleichung −n2 = 8λ(2λ − 1)2 mit λ = −2m2 , so ist die
obige elliptische Kurve vom Typ En und wir haben gemäß Satz 9 nur noch
nachzuweisen, dass der rationale Punkt P unendliche Ordnung besitzt. Dies
liefert aber sofort der Satz 5 von Nagell-Lutz. •
Im Verbleibenden wollen wir das Unmögliche möglich machen und nun doch
noch ein rechtwinkliges Dreieck mit Fläche eins konstruieren! Dabei können
wir nach obigem Korollar keine rationalen Seitenlängen fordern, wohl aber
algebraische. So ist das Dreieck mit den Seitenlängen √36 , √46 , √56 rechtwinklig
und besitzt Fläche eins. Allerdings war uns das zu einfach: Wir haben hier die
quadratische Homogenität von (27) ausgenutzt. Interessanter ist, ob uns dies
auch mit algebraischen Seitenlängen höheren Grades gelingen kann? Dieser
Frage sind Girondo et al.§ nachgegangen.
Wir beweisen nun (skizzenhaft) den folgenden Satz: Jede natürliche Zahl
n ist eine Kongruenzzahl über einem geeigneten reell-kubischen Zahlkörper.
Hierbei heißt eine endliche algebraische Erweiterung von Q ein Zahlkörper
†
J.S. Chahal, Congruent numbers and elliptic curves, American Mathematical Monthly
113 (2006) 308–317.
‡
A. Desboves, Sur l’emploi des identités algébriques dans la résolution, en nombres
entiers, des équations d’un degré supérieur au second, Comptes Rendus LXXXVII (1879)
159–161, 321-322.
§
E. Girondo, G. González-Diez, E. González-Jiménez, R. Steuding, J. Steuding, Right triangles with algebraic sides and elliptic curves over number fields, Math. Slovaca 59 (2009), 299-306.
10. Das Kongruenzzahlproblem
69
und tatsächlich lässt sich vieles aus der Theorie der elliptischen Kurven von
Q auf solche Zahlkörper übertragen. Wir nennen dabei eine natürliche Zahl n
eine Kongruenzzahl bzgl. eines Zahlkörpers K, wenn es unendlich viele
rechtwinkliges Dreiecke mit Fläche n und Seitenlängen in K gibt. Für den
Beweis des oben angebeenen Satzes erklären wir zu n ∈ N die Zahl λ = λ(n)
als die eindeutige reelle Lösung der kubischen Gleichung (29), also
32λ3 − 32λ2 + 8λ + n2 = 0.
Dann gilt
λ = λ(n) =
wobei
κ = κ(n) =
q
3
1
1
1
+ κ+
,
3 12
3κ
p
−8 − 27n2 + 3 48n2 + 81n4 ;
dabei wählen wir κ als die eindeutige reelle dritte Wurzel, welche für alle n
negativ ausfällt. Mit ein wenig Rechnerei finden wir den Punkt P = (x, y) auf
der elliptischen Kurve En (Q(λ)), wobei die Koordinaten durch
1
x =
{256 + 992n2 + 65n4 + (1024 − 2688n2 − 28n4 )λ
4(n2 − 16)2
+(1024 + 1920n2 + 4n4 )λ2 },
1
{−16384 + 72704n2 + 80960n4 + 2868n6 − n8
y =
2
32(n − 16)3
+(196608 − 462848n2 − 145152n4 − 1456n6 )λ
+(196608 + 421888n2 + 100608n4 + 208n6 )λ2 }
gegeben sind. Es verbleibt zu zeigen, dass der Punkt Pλ ∈ En (Q(λ)) unendliche Ordnung besitzt. Tatsächlich ist das Torsionsverhalten über Zahlkörpern
diffiziler als über Q, jedoch mag man hier ausnutzen, dass die Abbildung
√
(x, y) → (−x, iy) mit i = −1 ein Endomorphismus auf En definiert und also
En komplexe Multiplikation bzgl. Z[i] besitzt. Mit Schranken für die Ordnung
der Torsionsuntergruppe¶ zeigt sich, dass P wirklich von unendlicher Ordnung
auf En (Q(λ)) ist. (Tatsächlich benutzt man hierzu so genannte Divisionspolynome; die Details finden sich in dem entsprechenden Aufsatz von Girondo et
al.) Damit besitzt En (Q(λ(n))) positiven Rang und unser Satz folgt aus dem
Zahlkörperanalogon von Satz 9. Dank dieser expliziten Konstruktion ist also
etwa n = 1 eine Kongruenzzahl bzgl. des Zahlkörpers Q(α), wobei
q
√
1
1 3
1
−35 + 3 129 + p
.
α= +
√
3
3 12
3 −35 + 3 129
Das folgende Dreieck hat Seitenlängen in eben diesem Zahlkörper und besitzt
Flächeninhalt eins:
¶
D. Prasad and C.S. Yogananda, Bounding the torsion in CM elliptic curves. C. R.
Math. Acad. Sci. Soc. R. Can. 23 (2001), no. 1, 1–5.
70
ELLIPTISCHE KURVEN
15 817 675
6 642 426
138 048
62 195
380 736 Α2
151 008 Α
+
1
62 195
62 195
779
890
3776 Α2
1879 Α
-
+
1335
1335
76 896 448 Α2
5 151 011 Α
+
3 321 213
16 606 065
Literaturverzeichnis
[1] R. Crandall, C. Pomerance, Prime Numbers: A Computational Perspective, Springer
2005
[2] D. Hankerson, A. Menezes, S. Vanstone, Guide to Elliptic Curve Cryptography,
Springer 2004
[3] M. Hindry, J.H. Silverman, Diophantine Geometry: An Introduction, Springer 2000
[4] A.W. Knapp, Elliptic Curves, Princeton University Press 1992
[5] D.E. Knuth, The art of computer programming, vol. 2; Seminumerical Algorithms,
Addison-Wesley 1997, 3rd ed.
[6] N. Koblitz, A Course in Number Theory and Cryptography, Springer 1987
[7] J.H. Silverman, The Arithmetic of Elliptic Curves, Springer 2009, 2nd edition
[8] J.H. Silverman, J. Tate, Rational points on elliptic urves, Springer 1992
[9] J. Steuding, Diophantine Analysis, CRC-Press/Chapman Hall 2005
[10] M. Stoll, Elliptische Kurven I + II, online -Skript erhältlich unter
http://www.faculty.iu-bremen.de/stoll/vorlesungen/Elliptische-Kurven-SS2000.pdf
[11] L.C. Washington, Elliptic Curves. Number Theory and Cryptography, CRCPress/Chapman Hall, 2nd ed. 2008
71