3.6 Marktnachfrage und Elastizität

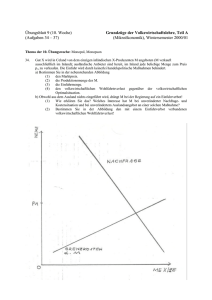
3.6 Marktnachfrage und Elastizität
Bisher haben wir uns ausschließlich mit dem Nachfrageverhalten einzelner Konsumenten
beschäftigt. Sowohl aus betriebswirtschaftlicher als auch aus volkswirtschaftlicher Sicht ist
aber das Nachfrageverhalten aller Konsumenten zusammengenommen interessant. Dieses
ergibt sich sehr einfach aus der Summe der Nachfrageverhalten der einzelnen
Konsumenten.
n
X ( p, m1, ... , mn) :=
∑ x k ( p, mk )
k =1
Diese Funktion wird auch Marktnachfragefunktion genannt. Die Marktnachfrage hängt
von den Preisen und der gesamten Einkommensverteilung ab.
Manchmal werden wir von der Annahme eines repräsentativen Konsumenten ausgehen.
Darunter versteht man eine Situation, in der die Marktnachfrage nur von der Summe der
Einkommen abhängt. Wenn es nur auf die Summe ankommt, ist die Verteilung der
Einkommen auf die einzelnen Konsumenten ohne Belang. Eine solche Situation tritt z.B.
auf, wenn wir von quasilinearen Präferenzen ausgehen, v(x1) + x2 . Dann ist die
Marktnachfragefunktion nach dem ersten Gut gar nicht vom Einkommen abhängig. Und
die Marktnachfragefunktion nach dem zweiten Gut hängt nur von der Summe der
Einkommen ab, solange alle Konsumenten alle Güter in positiven Mengen nachfragen (vgl.
Aufgabenblatt 5).
Wir können die Marktnachfrage aus den einzelnen Nachfragen der Konsumenten nach
einem Gut graphisch ermitteln, wenn wir die anderen Preise und alle Einkommen konstant
halten:
Nachfrage nach einem Gut
A+B
B
Xi(⋅)
A
C
D Preis
Hier haben wir die Nachfragefunktionen zweier Konsumenten abgetragen. Die des ersten
ist durch die Kurve von A nch C charakterisiert, die des zweiten durch die Kurve von B
nach D (zur Vereinfachung als Geraden). Die stark gezeichnete Kurve ist dann die
Marktnachfrage. Sie entsteht durch die graphische Addition der beiden einzelnen
Nachfragekurven über der Preisachse (hier also vertikal).
In manchen Anwendungen ist es jedoch hilfreich, den Preis an der vertikalen und die
Menge an der horizontalen Achse abzubilden. In einer solchen Graphik ergibt sich die
Marktnachfragefunktion natürlich als horizontale Addition (vgl. Varian).
Die Kurve, die in der obigen Graphik die Marktnachfrage wiedergibt, läßt uns graphisch
leicht herausfinden, wieviel von einem Gut, X, bei einem vorgegebenen Preis, p,
nachgefragt wird: X(p). Wir können jedoch auch anders herum fragen: Bei welchem Preis,
p, wird eine vorgegebene Menge des Gutes, X, nachgefragt. Auch darauf gibt die
Nachfragekurve eine Antwort. Wenn uns dieser Aspekt interessiert (welcher Preis gehört
zu welcher Menge?), interpretieren wir die Kurve als inverse Nachfragefunktion oder
Preis-Absatz-Funktion. Die Antwort wird dann mit P(X) gekennzeichnet. Der Name
"inverse Nachfragefunktion" kommt einfach daher, daß die Preis-Absatz-Funktion im
mathematischen Sinn die inverse (oder Umkehr-) Funktion der Nachfragefunktion ist.
Wenn die Interpretation der Nachfragekurve als Preis-Absatz-Funktion im Vordergrund
steht, trägt man naheliegenderweise die Menge horizontal ab.
Preis
P(⋅)
C
A+B
Menge
Zum Abschluß dieses Kapitels wollen wir noch auf den Begriff der Elastizität der
Nachfrage eingehen. Diesen Begriff kann man sowohl auf die Marktnachfrage als auch auf
die Nachfrage der einzelnen Konsumenten beziehen. Man kann ihn auf die Preise und auf
das Einkommen beziehen. Beginnen wir mit der Preis-Elastizität der Nachfrage:
Sie gibt Antwort auf die Frage, um wieviel Prozent sich die Nachfrage eines Gutes ändert,
wenn sich der entsprechende Preis um ein Prozent erhöht. Die prozentuale Änderung des
Preises läßt sich als
∆p
p
schreiben, die prozentuale Änderung der Nachfrage nach z.B. dem ersten Gut als
∆ x1
.
x1
Die Nachfrage wird sich dann pro einprozentige Steigerung des Preises um
∆ x1 p
x1 ∆ p
Prozent ändern. Dies ist die Preis-Elastizität der Nachfrage nach dem ersten Gut. Sie mißt
demnach die Sensitivität der Nachfrage bezüglich ihres Preises. Es gibt natürlich noch ein
anderes Maß für diese Sensitivität: die Ableitung der Nachfrage nach ihrem Preis. Die
Elastizität hat den Vorteil, nicht von den Maßen abzuhängen, in denen Preis und Menge
gemessen werden. Dies hat z.B. bei internationalen Vergleichen einen großen Vorteil.
Die Elastizitäten werden später in der Vorlesung wie auch insgesamt im Studium eine
wichtige Rolle spielen. Beispielsweise werden sich bei wenig preiselastischen Nachfragen
hohe Preissetzungsspielräume für die Unternehmen ergeben. Außerdem hängt die
Überwälzungsmöglichkeit von Steuern wesentlich von dieser Elastizität ab usw.
Kommen wir kurz auf den Zusammenhang zwischen Ableitung der Nachfrage nach dem
Preis und dem Begriff der Preis-Elastizität zurück. Wir können den obigen Ausdruck für
diese Elastitzität auch schreiben als
∆ x1 p
∆ p x1
Der erste Faktor ist gerade die Ableitung der Nachfrage nach dem Preis. Wir haben bisher
den Preis, hier des ersten Gutes, mit p bezeichnet. Diesen werden wir jetzt wieder genauer
mit p1 angeben. Dann kann man die Preis-Elastizität auch schreiben als
∂x1
p1
( p1 , p2 , m)
.
∂p1
x1 ( p1 , p2 , m)
Über diese Formel läßt sich die Elastizität der Nachfrage nun berechnen, wenn man die
Nachfragefunktion kennt.
Man beachte, daß diese Elastizität bei normalen Gütern eine negative Größe ist. Oft werden
Nachfragefunktionen bzgl. ihrer Preis-Elastizität miteinander verglichen. Man sagt dann,
daß eine Nachfrage elastischer als eine andere ist, wenn der Betrag (Absolutwert) der
Elastizität der einen größer ist! In dieser Sprechweise sind also die elastischeren
Nachfragen diejenigen, die sensitiver auf Preisänderungen reagieren.
Eng verwandt mit der Preis-Elastizität ist die sogenannte Kreuzpreis-Elasitizität der
Nachfrage nach einem Gut, z. B. Gut 1. Damit wird die Frage beantwortet, um wieviel
Prozent sich die Nachfrage nach diesem Gut ändert, wenn sich der Preis eines anderen
Gutes, hier Gut 2, um ein Prozent erhöht:
∂x1
p2
( p1 , p2 , m)
∂p2
x1 ( p1 , p2 , m)
Die Begründung dafür, daß dieser Ausdruck die Antwort auf die erwähnte Frage ist, ergibt
sich völlig analog zu der Begründung für die Preis-Elastizität, die in diesem
Zusammenhang zur Klarstellung auch oft Eigenpreis-Elastizität genannt wird.
Schließlich haben wir noch die Einkommens-Elastizität der Nachfrage, die angibt, um
wieviel Prozent sich die Nachfrage ändert, wenn sich das Einkommen um ein Prozent
erhöht:
∂x1
m
( p1 , p2 , m)
∂m
x1 ( p1 , p2 , m)
Mit Hilfe dieses Maßes für die Sensitivität der Nachfrage bzgl. des Einkommens wird oft
eine Güterklassifizierung vorgenommen. Man sagt, ein Gut sei ein Luxusgut, wenn die
Einkommenselastizität der Nachfrage für dieses Gut größer als eins ist. Man kann dies
auch so ausdrücken, daß sich die Nachfrage nach Luxusgütern überproportional zum
Einkommen erhöht.