Uebungsblatt 4 - of Gerald Pech

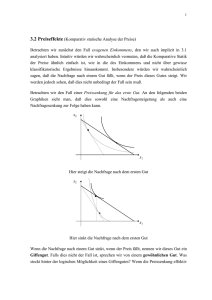
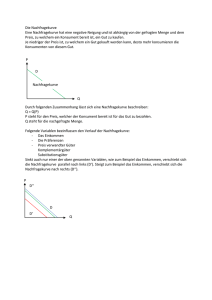
Johannes Gutenberg-Universität Mainz
Grundzüge der Mikroökonomie BA
SS 2010
Tutoriumsaufgaben
Übungsblatt 4
4.1. Verbraucherverhalten
Die Präferenzen eines Konsumenten für Benzin (x = Menge Benzin in Litern) und aller anderen
Konsumgüter (y) können durch die Nutzenfunktion U = x y repräsentiert werden. Ursprünglich
betrage der Preis von Benzin 1 $. Der Preis von y sei auf 1$ normiert. Durch eine Benzin-Steuer
erhöhe sich der Preis auf 4$ pro Liter Benzin. Der Konsument habe ein Einkommen von 10$.
a) Wie viel Benzin konsumiert der Verbraucher, wenn keine Steuer erhoben wird? Wie viel Benzin
konsumiert er, wenn die Steuer erhoben wird? Welchen Wert nimmt die Nutzenfunktion jeweils an?
b) Zeichnen Sie ein Diagramm in dem Sie die beiden Budgetrestriktionen und die Optimalpunkte
eintragen. Skizzieren Sie weiter zwei Indifferenzkurven mit denen Sie den Einkommens- und
Substitutionseffekt der steuerinduzierten Preiserhöhung darstellen können.
MU x ! p x

c) Benutzen Sie die Optimalitätsbedingung für den Konsumenten
und die
MU y p y
Budgetrestriktion I = px x + py y, um für die vorgegebenen Preise von px=4 und py = 1 die
Nachfrage des Konsumenten nach dem Gut x als Funktion des Einkommens zu schreiben.
Schreiben Sie ebenfalls die Nachfrage des Konsumenten nach y als Funktion des Einkommens!
d) (etwas schwieriger!) Benutzen Sie Ihre Ergebnisse aus Teil c) dieser Aufgabe, um die folgenden
Fragen zu beantworten: Wie groß müsste das Einkommen sein, damit der Konsument bei einem
Benzin-preis von 4$ im Optimum denselben Nutzenwert erzielt wie in der Situation in der der
Benzinpreis 1$ und das Einkommen 10$ betrug? Wie hoch ist das Einkommen, das der Konsument
bräuchte um sich bei einem Benzinpreis von 4$ dasselbe Güterbündel wie bei einem Benzinpreis
von 1$ zu kaufen? Tragen Sie auch diese Budgetgerade in den Graphen ein. Woher kommt der
Unterschied zwischen beiden Einkommensgrößen?
4.2. Nachfragekurve
Gut x1 und Gut x2 sind perfekte Komplemente (d.h. der Konsument will beide im gleichen
Verhältnis konsumieren).
a) Zeichnen Sie eine beliebige Indifferenzkurvenschar und kennzeichnen Sie für unterschiedliche
Preise für x1 die optimalen Konsumpunkte in einem Diagramm mit x2 auf der Ordinate und x1 auf
der Abszisse.
b) Geben Sie in allgemeiner Form die optimale Allokation des Einkommens I für die Güter x1 und
x2 an, wenn die Preise p1 und p2 betragen. D.h. drücken Sie die Nachfrage nach x1 als Funktion des
Einkommens I und den Preisen p1 und p2 aus.
c) Nehmen Sie an, das Einkommen sei I = 8 und p2 =1. Zeichen Sie die Nachfragekurve des
Konsumenten, indem Sie die Probewerte p1 = 5, p1 = 3 und p1= 1 einsetzen. Welches ist die
maximale Menge von Gut x1 welche bei einem Preis von p1=0 gekauft würde?