3.2 Preiseffekte (Komparativ statische Analyse der Preise
Werbung

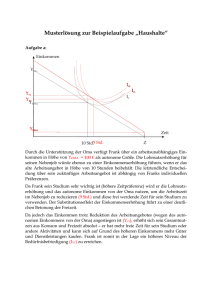
1 3.2 Preiseffekte (Komparativ statische Analyse der Preise) Betrachten wir zunächst den Fall exogenen Einkommens, den wir auch implizit in 3.1 analysiert haben. Intuitiv würden wir wahrscheinlich vermuten, daß die Komparative Statik der Preise ähnlich einfach ist, wie in die des Einkommens und nicht über gewisse klassifikatorische Ergebnisse hinauskommt. Insbesondere würden wir wahrscheinlich sagen, daß die Nachfrage nach einem Gut fällt, wenn der Preis dieses Gutes steigt. Wir werden jedoch sehen, daß dies nicht unbedingt der Fall sein muß. Betrachten wir den Fall einer Preissenkung für das erste Gut. An den folgenden beiden Graphiken sieht man, daß dies sowohl eine Nachfragesteigerung als auch eine Nachfragesenkung zur Folge haben kann. x2 • • x1 Hier steigt die Nachfrage nach dem ersten Gut x2 • • x1 Hier sinkt die Nachfrage nach dem ersten Gut Wenn die Nachfrage nach einem Gut sinkt, wenn der Preis fällt, nennen wir dieses Gut ein Giffengut. Falls dies nicht der Fall ist, sprechen wir von einem gewöhnlichen Gut. Was steckt hinter der logischen Möglichkeit eines Giffengutes? Wenn die Preissenkung effektiv 2 wird, ist die ursprüngliche marginale Zahlungsbereitschaft für das Gut 1 größer als der neue reale Preis des ersten Gutes. Daher lohnt es sich zunächst, mehr von dem ersten Gut zu kaufen. Aber implizit ist das Einkommen gestiegen. Durch den gesunkenen Preis kann man sich mehr leisten. Das Einkommen ist mehr wert. Dieses "zusätzliche" Einkommen kann nun darauf verwendet werden, mehr von beiden Gütern zu kaufen. Dabei ist es möglich, daß man lieber von dem ersten Gut weniger kaufen will, um "viel mehr" von dem zweiten Gut kaufen zu können. Dieser implizite "Einkommenseffekt" einer Preisänderung wird im folgenden Abschnitt näher untersucht. Wir werden dann auch leicht einsehen können, daß ein Gut nur dann ein Giffengut sein kann, wenn es ein inferiores Gut ist. Verbindet man alle Punkte, die sich als nachgefragte Güterbündel bei variierendem Preis für das erste Gut (cet.par.) ergeben, so nennt man das Ergebnis Preis-Konsum-Kurve. Betrachtet man die Abhängigkeit der Nachfrage nach einem Gut in Abhängigkeit des eigenen Preises, so legt dieser funktionale Zusammenhang die Nachfragekurve für dieses Gut fest. Bisher haben wir also definitionsgemäß festgelegt, daß für gewöhnliche Güter unsere Intuition richtig ist: ∂xi ≤0 ∂pi Es gibt jedoch die Möglichkeit, daß die Nachfrage nach einem Gut steigt, wenn der Preis steigt. Damit haben wir untersucht, wie die Nachfrage auf eine Änderung des "eigenen" Preises reagiert. Was passiert mit der Nachfrage eines Gutes, wenn der Preis eines anderen Gutes steigt? Darüber sagt die Theorie fast gar nichts aus. Es ist sowohl möglich, daß die Nachfrage nach Gut i steigt, wenn ein anderer Preis pj steigt, als auch, daß sie fällt. Wenn ∂xi >0 ∂p j gilt, sagt man, daß die Güter i und j Bruttosubstitute sind. Falls die umgekehrte Ungleichung gilt, spricht man von Bruttokomplementen. (Warum wohl?) Wir kommen nun zu der Analyse endogenen Einkommens. Hier ist also m = p1ω1 + p2ω2. Betrachten wir eine Preissenkung für das erste Gut. 3 Die Nachfragefunktion hängt nun über zwei Effekte von dem gesunkenen Preis p1 ab. Der erste Effekt entspricht gerade dem Effekt bei exogenem Einkommen. Aber hinzu tritt jetzt eine direkte und explizite Einwirkung auf das Einkommen. x2 A• • C • B x1 Der Übergang von A nach C entspricht dem oben besprochenen "üblichen" Preiseffekt. Der gesunkene Preis hat nun jedoch zusätzlich den Effekt, daß das Einkommen gesunken ist. Der Übergang von C nach B entspricht diesem Effekt, dem sogenannten AusstattungsEinkommenseffekt. Der gesamte Effekt der Preisänderung entspricht also dem Übergang von A nach B. Mathematisch lassen sich die beiden Effekte sofort herausfiltern, wenn man die Nachfragefunktion nach p1 ableitet: xi ( p1, p2, m ( p1, p2 )) ∂xi ∂xi ∂m ∂xi ∂xi + = + ω1 ∂p1 ∂m ∂p1 ∂p1 ∂m Wir wollen hier kurz auf die Arbeits-Konsum Entscheidung eingehen (Beispiel 5 aus 2.2). Dort war ω1 die Ausstattung mit Zeit. Gehen wir wie dort davon aus, daß ω2 = 0, und zusätzlich, daß das exogene Einkommen m = 0. In diesem Kontext ist x1(.,.,.) die Nachfrage nach Freizeit. Entsprechend ist a ( p1, p2, m ( p1, p2 )) = ω1 - xi ( p1, p2, m ( p1, p2 )) das Angebot an Arbeitszeit des Konsumenten. Wie reagiert nun das Arbeitsangebot des Konsumenten auf eine Erhöhung des Lohnsatzes p1 ? Die Antwort ergibt sich am einfachsten aus einer mathematischen Betrachtung: ∂x ∂x ∂a = − 1 − 1 ω1 ∂p1 ∂p1 ∂m Wie wir schon einmal in 2.4 im Zusammenhang mit der Betrachtung von steuerlichen Gesichtspunkten gesehen haben, ist die Antwort nicht eindeutig. Selbst, wenn wir 4 unterstellen, daß Freizeit ein normales Gut ist, daß also ∂x1 ∂x > 0 gilt, woraus dann 1 < 0 ∂m ∂p1 folgt, wie wir noch sehen werden, ist die Antwort nämlich nicht klar. Der erste Summand ist dann nämlich insgesamt positiv, während der zweite Summand negativ ist. Wissen wir nun mehr als in 2.4? Jedenfalls wissen wir nicht, ob das Arbeitsangebot steigt oder fällt. Aber wir wissen nun, vovon dies abhängt. Es hängt davon ab, ob der erste Term (der normale Preiseffekt) größer ist als der zweite (der Ausstattungs-Einkommenseffekt) oder vice versa. Und was steht nun hinter diesen beiden Effekten ökonomisch? Überlegen Sie mal! Wir sind hier wieder in einer Situation, in der wir durch ein Modell verschiedene Gesichtspunkte aufdecken können, die, wenn wir sie dann kennen, jedem einleuchten, so daß man versucht ist, zu sagen, daß man die Modellbetrachtung gar nicht gebraucht hat. Dies ist jedoch eine Form des "Nachher ist man schlauer". Versuchen Sie, sich nochmals in die Lage zu versetzen, bevor Sie die beiden Effekte kennengelernt haben. Welche Antwort hätten Sie dann gegeben? Hätten Sie überhaupt eine geben können? Seien Sie mal ganz ehrlich mit sich selbst.