2. Übung Aufgaben
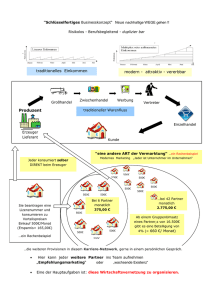
Werbung

Aufgabe 4 Es bezeichne pi den Preis des i-ten Gutes, xi die Menge des i-ten Gutes und m das Einkommen. a Stellen Sie die Budgetgerade des Haushalts im Zwei-Güterfall auf! b Wieviele Einheiten Gut 1 könnte sich der Haushalt leisten? c Skizzieren und beschriften Sie eine Budgetgerade im x1 -x2 -Raum! d Auf wieviele Einheiten Gut 1 hat der Haushalt zu verzichten, wenn er eine zusätzliche Einheit Gut 2 konsumieren möchte? e Wie ändert sich die Budgetgerade, wenn das Einkommen oder der Preis von Gut 1 steigt? 1 von 4 Aufgabe 5 Gegeben sind folgende Budgetgleichungen: 2x1 + 4x2 = 40, 2x1 + 4x2 = 20 und x1 + 4x2 = 20. a Bestimmen Sie die Anstiege und Schnittpunkte mit den Koordinatenachsen! b Zeichnen Sie die Budgetgeraden! c Existieren Güterkombinationen, welche mit jeder der drei Budgetgleichungen konsumierbar sind? 2 von 4 Aufgabe 6 Ein Haushalt kann sich gerade 2 Einheiten des Gutes 1 und 3 Einheiten des Gutes 2 leisten. Alternativ lässt sein Einkommen aber auch 3 Einheiten Gut 1 und eine Einheit Gut 2 zu. a Wieviele Einheiten Gut 2 könnte der Haushalt konsumieren, wenn er sein gesamtes Einkommen nur dafür ausgeben würde? 3 von 4 Aufgabe 7 Ein Haushalt verfügt über ein Einkommen von 120 Geldeinheiten. Er konsumiert 30 Einheiten Gut 1 und 15 Einheiten Gut 2. Gut 1 kostet 3 Geldeinheiten, Gut 2 2 Geldeinheiten. a Wenn das Einkommen um 20 Einheiten steigt, der Preis des Gutes 1 um 1 Geldeinheit steigt und der von Gut 2 um 20% sinkt, kann der Haushalt dann seine Konsumgewohnheiten beibehalten? 4 von 4