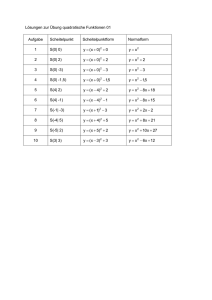
Aufgabe 1

Technische Universität München
Institut für Informatik
Prof. Tobias Nipkow, Ph.D.
Dr. Clemens Ballarin
Vorlesung Logik
Sommersemester 2003
Musterlösung zu Übungsblatt 1
Aufgabe 1
a) Nein.
Gegenbeispiel:
0 ← 1 ← 2 ← 3 ← ...
3
6
A
Q K
k
Q A
QA
⊥
R = {(⊥, n) | n ∈ N} ∪ {(n + 1, n) | n ∈ N}, R ⊆ (N ∪ {⊥}) × N
∗
R ist terminierend, für alle x ∈ N ∪ {⊥} gilt x −→ 0
R ist unbeschränkt, da es für das Elemente ⊥ keine obere Grenze der von ⊥
n
ausgehenden Pfade gibt: ∀n. ⊥ −→ 0
b) beschränkt ⇒ terminierend: trivial
terminierend ⇒ beschränkt: mit fundierter Induktion
Induktions-Hypothese
z
}|
{
+
Regel: ∀x ∈ A. (∀y ∈ A. x −→ y ⇒ P (y)) ⇒ P (x)
∀x ∈ A. P (x)
n
Definition von beschränkt: ∀x. ∃n. 6 ∃y. x −→ y
n
⇒ P (x) = ∃n. 6 ∃y. x −→ y
Beweis:
Vorraussetzung: −→ ist endlich verzweigt
+
n
Induktions-Hypothese (IH): ∀y. x −→ y ⇒ ∃n. 6 ∃y. x −→ y
n
zu zeigen: ∃n. 6 ∃y. x −→ y
Fallunterscheidung:
• x ist in Normalform (NF). Dann wählen wir n = 1.
• x ist nicht in NF. Nach IH gibt es für jeden Nachfolger von x (also
auch für jeden direkten Nachfolger) eine Schranke n0 , so daß es kein
y gibt, das n0 Schritte (oder mehr) von x entfernt ist. Da es nach
Vorraussetzung nur endlich viele direkte Nachfolger von x geben kann,
existiert das Maximum nmax dieser Schranken.
Wir wählen n = 1 + nmax
1
Aufgabe 2
a) Gilt nicht.
Gegenbeispiel: R = {(n, n + 1) | n ∈ N}, R ⊆ N × N
0 → 1 → 2 → ...
R ist azyklisch und endlich verzweigt, terminiert aber nicht.
b) Gilt. Zu zeigen ist:
+
−→ hat genau dann keine unendlich absteigende Kette,
wenn −→ keine hat.
+
⇔ −→ hat genau dann mindestens eine unendlich absteigende Kette,
wenn −→ mindestens eine unendlich absteigende Kette hat.
+
−→ ⇒ −→ :
+
+
+
Sei x −→ y −→ . . . eine unendlich absteigende Kette für −→. Nach
+
Definition von −→ gibt es Elemente xi mit x −→ x1 −→ · · · −→ y −→
x01 −→ . . . die eine unendlich absteigende Kette für −→ bilden.
+
−→ ⇒ −→ :
Sei x −→ y −→ . . . eine unendlich absteigende Kette für −→. Dann ist
+
+
+
x −→ y −→ . . . ebenfalls eine unendlich absteigende Kette für −→, da
+
−→ ⊆ −→.
Aufgabe 3
Die Relation lässt sich schreiben als
−→ = {2k −→ 3k | k ∈ N+ } ∪ {11k −→ 7]5k | k ∈ N+ }
a) alle reduzierbaren Zahlen haben die Form
2n 11m · x mit n, m ∈ N, x ∈ N+ , n + m > 0, 2 - x, 11 - x
m + n wird bei jeder Reduktion um genau 1 verringert, also terminiert −→.
b) die Menge der irreduziblen Elemente ist
{n ∈ N | ggT (n, 2) = 1 ∧ ggT (n, 11) = 1}
c) 726 = 2 · 3 · 112 −→ 32 · 112 −→ 32 · 5 · 11 −→ 32 · 52
32 52 ist irreduzibel, d.h. 32 52 ist eine NF von 726. Da −→ konfluent ist, ist es die
eindeutige NF von 726: 726 ↓= 32 52
d) 22 = 2 · 11 −→ 2 · 5 = 10, und damit auch 10 ←→ 22.
+
20 = 22 · 5 −→ 32 · 5
99 = 32 · 11 −→ 32 · 5
+
∗
also 20 −→ 32 · 5 ←− 99 und damit auch 20 ←→ 99
2
Aufgabe 4
Beweis
∗
1) ←→ ist Äquivalenzrelation:
Transitivität: per Defintion
Reflexivität: per Definition
Symmetrie:
←→ ist symmetrisch und ∗ erhält Symmetrie:
∗
a1 ←→ an ⇔ a1 ←→ a2 ←→ · · · ←→ an
⇔ an ←→ · · · ←→ a2 ←→ a1
∗
⇔ an ←→ a1
∗
2) ←→ ist die kleinste Äquivalenzrelation mit −→ ⊆ R:
Sei R Äquivalenzrelation mit −→ ⊆ R
∗
zu zeigen: ←→ ⊆ R
∗
a1 ←→ an ⇒
⇒
⇒
⇒
a1 ←→ a2 ←→ · · · ←→ an
(ai , ai+1 ) ∈ R ∨ (ai , ai+1 ) ∈ R−1 = R ∀i
(ai , ai+1 ) ∈ R
(a1 , an ) ∈ R
Aufgabe 5
eindeutige Normalform ⇒ normalisierend (nach Definition)
konfluent:
Wäre −→ nicht konfluent, gäbe es ein Element
mit mehr als einer Normalform
normalisierend + konfluent ⇒ eindeutige Normalform
Satz aus der Vorlesung:
Elemente konfluenter Relationen haben höchstens eine Normalform
normalisierend:
Jedes Element hat mindestens eine Normalform
=⇒ Jedes Element besitzt eine eindeutige Normalform.
3