Grundlagen der Theoretischen Informatik

1
2
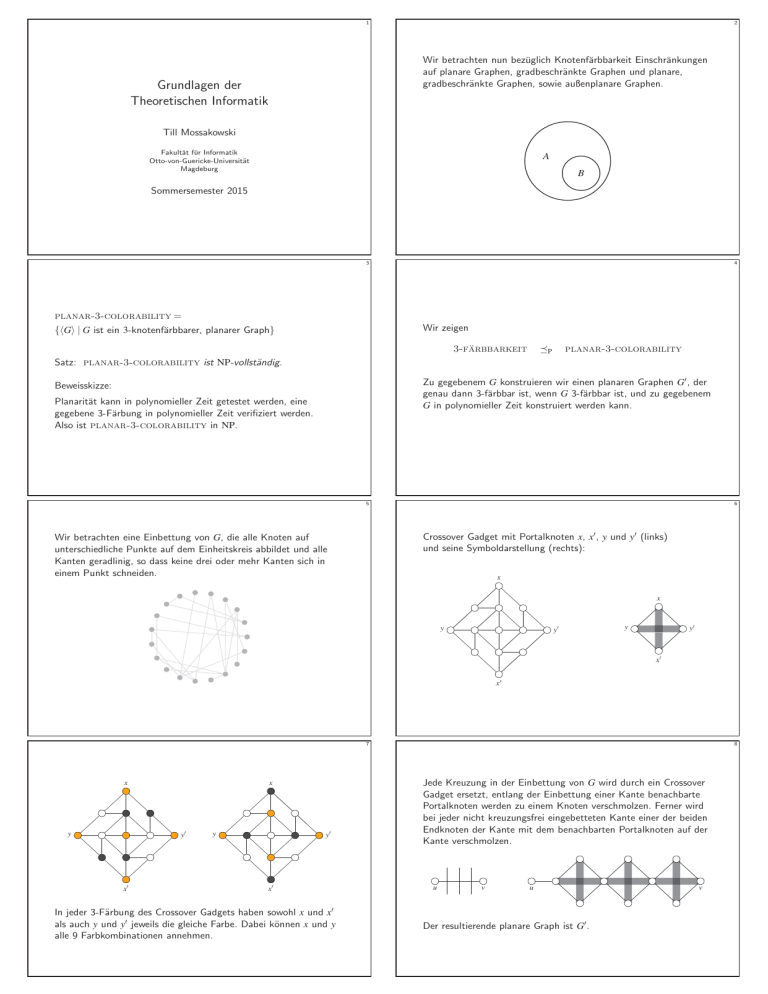
Wir betrachten nun bezüglich Knotenfärbbarkeit Einschränkungen
auf planare Graphen, gradbeschränkte Graphen und planare,
gradbeschränkte Graphen, sowie außenplanare Graphen.
Grundlagen der
Theoretischen Informatik
Till Mossakowski
Fakultät für Informatik
Otto-von-Guericke-Universität
Magdeburg
A
B
Sommersemester 2015
3
4
planar-3-colorability =
Wir zeigen
{G | G ist ein 3-knotenfärbbarer, planarer Graph}
P
3-färbbarkeit
planar-3-colorability
Satz: planar-3-colorability ist NP-vollständig.
Zu gegebenem G konstruieren wir einen planaren Graphen G , der
genau dann 3-färbbar ist, wenn G 3-färbbar ist, und zu gegebenem
G in polynomieller Zeit konstruiert werden kann.
Beweisskizze:
Planarität kann in polynomieller Zeit getestet werden, eine
gegebene 3-Färbung in polynomieller Zeit verifiziert werden.
Also ist planar-3-colorability in NP.
5
6
Crossover Gadget mit Portalknoten x, x , y und y (links)
und seine Symboldarstellung (rechts):
Wir betrachten eine Einbettung von G, die alle Knoten auf
unterschiedliche Punkte auf dem Einheitskreis abbildet und alle
Kanten geradlinig, so dass keine drei oder mehr Kanten sich in
einem Punkt schneiden.
x
x
y
y
y
y
x
x
7
x
x
y
y
x
y
y
x
In jeder 3-Färbung des Crossover Gadgets haben sowohl x und x
als auch y und y jeweils die gleiche Farbe. Dabei können x und y
alle 9 Farbkombinationen annehmen.
8
Jede Kreuzung in der Einbettung von G wird durch ein Crossover
Gadget ersetzt, entlang der Einbettung einer Kante benachbarte
Portalknoten werden zu einem Knoten verschmolzen. Ferner wird
bei jeder nicht kreuzungsfrei eingebetteten Kante einer der beiden
Endknoten der Kante mit dem benachbarten Portalknoten auf der
Kante verschmolzen.
u
v
u
Der resultierende planare Graph ist G .
v
9
10
Lemma: G ist genau dann 3-färbbar, wenn G 3-färbbar ist.
Definition:
Ein Graph heißt außenplanar, wenn er so kreuzungsfrei in die
Ebene eingebettet werden kann, dass alle Knoten auf dem Rand
des äußeren unbeschränkten Gebietes liegen.
Beweisskizze:
Eine 3-Färbung c von G liefert eine 3-Färbung von G und
umgekehrt, denn die Crossover Gadgets entlang einer Kante
propagieren die Farbe des verschmolzenen Endknotens zu dem zum
nicht verschmolzenen Endknoten benachbarten Portalknoten.
outerplanar-3-colorability =
{G | G ist ein 3-knotenfärbbarer, außenplanarer Graph}
u
Satz:
outerplanar-3-colorability ist in P.
v
11
12
Im Folgenden bezeichne Δ(G) den maximalen Grad eines Knotens
in einem Graphen G.
degree-restricted-3-colorability = {G, | G ist ein
Graph mit maximalem Knotengrad und G ist mit 3 Farben
knotenfärbbar}
Satz: [Brooks]
Ein Graph G, der weder vollständig noch ein Kreis ungerader Länge
ist, ist Δ(G)-knotenfärbbar, d.h.
Satz: degree-restricted-3-colorability ist NP-vollständig.
χ0 (G)
≤
Beweisskizze:
Δ(G)
Der maximale Knotengrad kann in polynomieller Zeit getestet
werden, eine gegebene 3-Färbung in polynomieller Zeit verifiziert
werden. Also ist degree-restricted-3-colorability in NP.
13
14
Gradreduktionsgadget mit 3 Portalknoten:
Wir zeigen
2
2
3-färbbarkeit
P
degree-restricted-3-colorability
Zu gegebenem G konstruieren wir einen Graphen G mit
maximalem Knotengrad = 4, der genau dann 3-färbbar ist, wenn
G 3-färbbar ist, und zu gegebenem G in polynomieller Zeit
konstruiert werden kann.
1
3
1
3
Das Gadget hat Maximalgrad 4. Bei allen 3-Färbungen des
Gadgets haben alle Portalknoten die gleiche Farbe.
15
Ein Gadget mit k Portalknoten lässt sich durch Kombination von
k − 2 Kopien des Gadget mit 3 Portalknoten erzeugen:
2
3
16
Jeden Knoten v in G mit Grad d > 4 ersetzen wir durch ein Gadget
mit d Portalknoten, die d inzidenten Kanten verbinden wir dabei
mit unterschiedlichen Portalknoten. Der resultierende Graph G hat
Maximalgrad höchstens 4.
4
Lemma: G ist genau dann 3-färbbar, wenn G 3-färbbar ist.
1
5
Beweisskizze:
Da stets alle Portalknoten eines Gadgets bei einer 3-Färbung die
gleiche Farbe haben, liefert eine 3-Färbung von G eine 3-Färbung
von G und umgekehrt.
17
Eine Färbung der Kanten eines Graphen G heißt zulässig, falls für
jeden Knoten alle zu ihm inzidenten Kanten verschiedene Farben
haben.
degree-4-restricted-planar-3-colorability = {G | G ist
ein mit 3 Farben knotenfärbbarer, planarer Graph, dessen Knoten
maximal Grad 4 haben}
Ein Graph ist k-kantenfärbbar, falls es eine zulässige
Kantenfärbung mit k Farben gibt.
Satz: degree-4-restricted-planar-3-colorability ist
NP-vollständig.
Das kleinste k, für das es eine zulässige Kantenfärbung von G mit
k Farben gibt, heißt der chromatische Index von G und wird mit
χ1 (G) bezeichnet.
Beweisskizze:
Zunächst wird Planarität forciert, dann der Grad reduziert.
Letzteres ist möglich, ohne die Planarität zu zerstören, da die
Gradreduktionsgadgets selbst planar sind und eine passende
Zuordnung der Portalknoten aus einer Einbettung abgeleitet
werden kann.
18
kantenfärbbarkeit = {G, k | G ist k-kantenfärbbar}
Satz: [Vizing] Sei G ein einfacher Graph. Dann gilt
χ1 (G) ∈ {Δ(G), Δ(G) + 1}
19
20
Starke NP-Vollständigkeit
Zur Erinnerung: Beim Problem partition sind a1 , a2 , . . . , an ∈ N
gegeben und es ist zu entscheiden, ob es I ⊆ {1, 2, . . . , n} gibt,
so dass
∑ ai = ∑ ai
Satz: [Holyer] kantenfärbbarkeit ist NP-vollständig.
Zum Beweis des obigen Satzes zeigt man
i∈I
Lemma: 3-sat P kantenfärbbarkeit.
i∈I
partition =
{bin(a1 )# · · · #bin(an ) | ∃ I ⊆ {1, 2, . . . , n} so dass
∑ ai = ∑ ai }
i∈I
i∈I
21
H=
1
2
Die Laufzeit des Algorithmus ist polynomiell in n und H,
aber nicht polynomiell in der Länge der Eingabe, in der die
ganzzahligen Größen binär dargestellt sind!
n
∑ aj
j=1
B(i) = {b ≤ H | ∃ Ii ⊆ {1, 2, . . . , i} so dass
22
∑ aj = b}
Algorithmen für Probleme, die Zahlen beinhalten, nennen wir
pseudopolynomiell, wenn ihre Laufzeit bei unärer Kodierung der
Zahlen in der Eingabe polynomiell ist.
j∈Ii
1 B(0) ← {0}
2 for i ← 1 to n
3
do B(i) ← B(i − 1)
4
for j ← ai , ai + 1, ai + 2, . . . , H
5
do if (j − ai ∈ B(i − 1))
6
then B(i) ← B(i) ∪ {j}
Für n ∈ N0 bezeichne un(n) die unäre Kodierung von n.
unary-partition =
{un(a1 )# · · · #un(an ) | ∃ I ⊆ {1, 2, . . . , n} so dass
i∈I
i∈I
unary-partition ∈ P
23
24
Beispiele für stark NP-vollständige Probleme:
Definition:
Ein Entscheidungsproblem heißt stark NP-vollständig, wenn es
auch dann noch NP-vollständig ist, wenn wir nur Probleminstanzen
betrachten, in denen die Größe der vorkommenden Zahlen
polynomiell in der Länge der Eingabe ist.
∑ ai = ∑ ai }
• sat
• 3-sat
• nae-3-sat
• vertex-cover
• hamilton-kreis
• knotenfärbbarkeit
25
26
Parametrisierte Komplexität
3-cnf = {φ | φ ist eine Boolesche Formel in konjunktiver
Normalform, in der alle Klauseln aus drei Literalen
bestehen}
O(22k · n)
O(nk )
3-sat
⊆
3-cnf
⊆
Σ∗
⎧
⎪
⎨ k falls x = φ ∈ 3-cnf und in φ
kommen k Variablen vor
κ(x) =
⎪
⎩ 1 sonst
Definition:
Eine Parametrisierung der Wörter über einem Alphabet Σ ist eine
in polynomieller Zeit berechenbare Abbildung κ : Σ∗ → N.
Definition:
Ein parametrisiertes Problem ist gegeben durch eine Sprache
L ⊆ Σ∗ und eine Parametrisierung κ : Σ∗ → N.
(3-sat, κ)
27
28
Fixed-Parameter Tractability
Beweisskizze:
Für jede der 2k möglichen Belegungen der k Variablen können wir
jeweils in Linearzeit testen, ob die Formel bei der Belegung erfüllt
ist.
Definition:
Ein parametrisiertes Problem (L, κ) ist festparameterhandhabbar
(fixed-parameter tractable), falls es einen Algorithmus A, ein
Polynom p(n) und eine berechenbare Funktion f (n) gibt, so dass A
für alle x ∈ Σ∗ in Zeit
f (κ(x)) · p(|x|)
entscheidet, ob x ∈ L.
X1 = 0
Satz:
(3-sat, κ) ist festparameterhandhabbar.
29
knotenfärbbarkeit
κ(x) =
X1 = 1
⊆
Σ∗
k falls x = G, k
1 sonst
Satz:
Falls P = NP, so ist das parametrisierte Problem
(knotenfärbbarkeit, κ) nicht festparameterhandhabbar.