Hilfsblätter zu Automatisierte Antriebe - antriebstechnik.fh

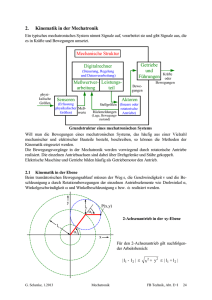
7.
Kinematik in der Mechatronik
Ein typisches mechatronisches System nimmt Signale auf, verarbeitet sie und gibt Signale aus, die
es in Kräfte und Bewegungen umsetzt.
Mechanische Struktur
Getriebe
und
Führungen
Digitalrechner
(Steuerung, Regelung
und Datenverarbeitung)
Meßwertver- Leistungsteil
arbeitung
physikalische
Größen
Sensoren
Bewegungen
Kräfte
oder
Bewegungen
Aktoren
(Erfassung
physikalischer MeßGrößen)
werte
Stellgrößen (lineare oder
rotatorische
Rückmeldungen
Antriebe)
(Lage, Bewegungszustand)
Grundstruktur eines mechatronischen Systems
Will man die Bewegungen eines mechatronischen Systems, das häufig aus einer Vielzahl
mechanischer und elektrischer Bauteile besteht, beschreiben, so können die Methoden der
Kinematik eingesetzt werden.
Die Bewegungsvorgänge in der Mechatronik werden vorwiegend durch rotatorische Antriebe
realisiert. Die einzelnen Antriebsachsen sind dabei über Drehgelenke und Stäbe gekoppelt.
Elektrische Maschine und Getriebe bilden häufig als Getriebemotor den Antrieb.
7.1 Kinematik in der Ebene
Beim translatorischen Bewegungsablauf müssen der Weg s, die Geschwindigkeit v und die Beschleunigung a durch Rotationsbewegungen der einzelnen Antriebselemente wie Drehwinkel α,
& realisiert werden.
Winkelgeschwindigkeit ω und Winkelbeschleunigung ε bzw. ω
y
l2
P(x,y)
α2
2-Achsenantrieb in der xy-Ebene
l1
α1
x
Für den 2-Achsenantrieb gilt nachfolgender Arbeitsbereich:
| l1 - l 2 | ≤
G. Schenke, 3.2003
Automatisierte Antriebe
2
x 2 + y ≤ | l1 + l 2 |
FB Technik, Abt. E+I
76
Durch die Geometrie ist der Weg mit seinen xy-Komponenten gegeben.
x = l1 ⋅ cos α1 + l 2 ⋅ cos (α1 + α 2 )
(7.1)
y = l1 ⋅ sin α1 + l 2 ⋅ sin (α1 + α 2 )
Die Geschwindigkeit mit den Komponenten x& und y& ist die 1. Ableitung des Weges nach der
Zeit.
x& = − l1 ⋅ ω1 ⋅ sin α1 − l 2 ⋅ (ω1 + ω 2 ) ⋅ sin (α1 + α 2 )
(7.2)
y& = l1 ⋅ ω1 ⋅ co s α1 + l 2 ⋅ (ω1 + ω 2 ) ⋅ co s (α1 + α 2 )
Die Beschleunigung mit den Komponenten &x& und &y& ist die 2. Ableitung des Weges nach der
Zeit.
& 1 ⋅ sin α1 − l 2 ⋅ (ω
&1 +ω
& 2 ) ⋅ sin (α1 + α 2 )
&x& = − l1 ⋅ ω
− l1 ⋅ ω12 ⋅ co s α1 − l 2 ⋅ (ω1 + ω 2 ) 2 ⋅ co s (α1 + α 2 )
& 1 ⋅ co s α1 + l 2 ⋅ (ω
&1 +ω
& 2 ) ⋅ co s (α1 + α 2 )
&y& = l1 ⋅ ω
(7.3)
− l1 ⋅ ω12 ⋅ sin α1 − l 2 ⋅ (ω1 + ω 2 ) 2 ⋅ sin (α1 + α 2 )
Für die Dimensionierung des Antriebes für jede Achse sind das entsprechende Widerstandsmoment MW(α), die Winkelgeschwindigkeit ω, die Winkelbeschleunigung und das Massenträgheitsmoment J(α) (bezogen auf die jeweilige Achse) erforderlich.
Da das Massenträgheitsmoment J(α) vom Drehwinkel α abhängt, ist es während des Bewegungsvorganges auch zeitabhängig.
Das Antriebsdrehmoment M der jeweiligen Achse muß exakt nach Gl. 7.4 berechnet werden.
dω 1
dJ(α )
M = M W (α) + J(α) ⋅
+ ⋅ω⋅
(7.4)
dt 2
dt
Das Massenträgheitsmoment J(α) wird mit Hilfe des Steiner´schen Satzes berechnet.
Für die Dimensionierung von Antrieben in der Mechatronik ist häufig nur das größte Antriebsdrehmoment von Interesse. Hieraus können die größten Winkelbeschleunigungen bei maximaler
Nutzlast bzw. abhängig von der Nutzlast berechnet werden.
Im allgemeinen bestimmen die Beschleunigungsmomente die maximalen Antriebsdrehmomente
in der Mechatronik.
Aus Gl. 7.1 kann zunächst der Drehwinkel α1 und anschließend der Drehwinkel α2 berechnet
werden.
Aus Gl. 7.2 können bei bekannten Drehwinkeln α1 und α2 die Winkelgeschwindigkeiten ω1 und
ω2 berechnet werden.
Für Servoantriebe sind damit die Lage (Drehwinkel α) und die Drehzahl n (Winkelgeschwindigkeit ω) bestimmt. Für die maximale Antriebsleistung der Servoantriebe (Dimensionierung des
& 1 und ω
& 2 aus Gl.
Servoantriebes) müssen zusätzlich die maximalen Winkelbeschleunigungen ω
7.3 ermittelt werden.
7.2 Kinematik im Raum
r
r
r
Im Newton´schen Grundgesetz m ⋅ a = Σ F präsentiert die Kraft F die Kinetik des Systems, die
r
Masse m die Trägheit und die Beschleunigung a die Kinematik.
r
Die Bewegung eines realen Systems ist vollständig beschrieben, wenn der Ortsvektor r (t) für
alle Systemteile bestimmt ist. Für die meisten technischen Systeme muß diese Aufgabe nur
näherungsweise durch Modelle gelöst werden. Das einfachste Modell eines Körpers ist der
Massenpunkt. Die aktuelle Position eines Massenpunktes zu einem Zeitpunkt t ist durch nachfolgenden Ortsvektor gegeben:
r
r
r
r
(7.5)
r (t) = x(t) ⋅ e x + y(t) ⋅ e y + z(t) ⋅ e z
G. Schenke, 3.2003
Automatisierte Antriebe
FB Technik, Abt. E+I
77
P (t)
∆r (t)
y
P (t + ∆t)
r (t)
Bewegung eines Massenpunktes P
in einem kartesischen
Koordinatensystem
r (t + ∆t)
y (t)
ey
ez
0
ex
x
Die aktuelle Position auf der Bahnkurve,
die der Massenpunkt im Raum beschreibt,
ergibt sich zu einem Zeitpunkt t + ∆t als
z
r
x (t)
der Ortsvektor r (t + ∆t) , der gegenüber
r
r
r (t) einen Zuwachs um ∆ r (t) aufweist.
r r
r
Die drei Einheitsvektoren e x , e y und e z stehen senkrecht aufeinander. Das kartesische Koordinatensystem wird als im Raum ruhend oder geradlinig gleichförmig bewegt angenommen.
In einem kartesische Koordinatensystem (Inertialsystem) sind die Einheitsvektoren von der Zeit
unabhängig, deren Ableitungen nach der Zeit sind gleich Null.
r
In Matrizenschreibweise gilt für den Ortsvektor r (t) :
z (t)
 x(t) 


r
r (t) =  y(t) 


 z(t) 
(7.6)
r
r
Durch Ableitung des Ortsvektors r (t) nach der Zeit erhält man die Geschwindigkeit v (t) des
Massenpunktes P auf der Bahnkurve.
 x& (t) 


r
r
r
r
v(t) = x& (t) ⋅ e x + y& (t) ⋅ e y + z& (t) ⋅ e z =  y& (t) 


 z& (t) 
r
r
Durch Ableitung der Geschwindigkeit v (t) erhält man die Beschleunigung a (t) :
(7.7)
 &x&(t) 


r
r
r
r
a(t) = &x&(t) ⋅ e x + &y&(t) ⋅ e y + &z&(t) ⋅ e z =  &y&(t) 
(7.8)


 &z&(t) 
Der Geschwindigkeitsvektor tangiert stets die Bahnkurve und kann auch in einem sogn. natürlichen Koordinatensystem dargestellt werden.
G. Schenke, 3.2003
Automatisierte Antriebe
FB Technik, Abt. E+I
78
y
eb
Bahnkurve
an
ey
0
Mitbewegtes, natürliches
Koordinatensystem
∆r (t)
en
r (t)
ez
a
et
∆s a
t
a
r (t + ∆t)
x
ex
z
Im natürlichen Koordinatensystem ist
ein dem Massenpunkt begleitendes
orthogonales Dreibein mit den Koordinatenachsen t, n und b, die die
sogn. Schmiegungsebene festlegen.
Hierbei ist t die Tangentenrichtung in
der Schmiegungsebene, n ist die
Normalenrichtung in der Schmiegungsebene und b ist die Binormalenrichtung senkrecht zu t und n.
Im natürlichen Koordinatensystem gilt:
r
r
r
r
d r (t)
d r ds
v(t) =
=
⋅
= et ⋅ v
dt
ds dt
r
Dabei ist e t der Tangenteneinheitsvektor. Der Betrag der Geschwindigkeit ist:
r
ds
|v| = v =
=
dt
v 2x + v 2y + v 2z =
2
x& 2 + y& + z& 2
In natürlichen Koordinaten ausgedrückt beträgt die Beschleunigung:
r
r
r dv de t
d r
a(t) =
+
⋅ (e t ⋅ v) = e t ⋅
⋅v
dt
dt
dt
(7.9)
(7.10)
(7.11)
Für die Ableitung des Einheitsvektors in Tangentenrichtung nach der Zeit gilt:
r
r
r
de t
de t
de t ds
1 r
dϕ r
⋅
⋅v =
⋅ en ⋅ v
(7.12)
en ⋅ v =
=
=
R
ds
ds
dt
ds dt
r
Der Beschleunigungsvektor a (t) liegt immer in der Schmiegungsebene. Seine Komponenten in
Tangential- und Normalrichtung heißen Tangential- und Normalbeschleunigung.
r
r
r
r
v2 r
a(t) = v& ⋅ e t + ⋅ e n = a t + a n
R
(7.13)
R ist der Krümmungsradius der Bahnkurve. Die Normalbeschleunigung ist stets zum Krümmungsmittelpunkt M gerichtet, also immer eine Zentripetalbeschleunigung. Für den Betrag der
Beschleunigung gilt:
r
|a| = a =
a 2x + a 2y + a 2z =
G. Schenke, 3.2003
v& 2 +
v4
=
R2
a 2t + a 2n
Automatisierte Antriebe
(7.14)
FB Technik, Abt. E+I
79
Die Bewegung des starren Körpers im Raum kann beschrieben werden, wenn die Lage von zwei
beliebigen Punkten P1 und P2 des starren Körpers verfolgt wird. Die voneinander abhängigen
r
r
Ortsvektoren r1 und r2 erfordern sechs Koordinatenangaben.
Die Lage des starren Körpers im Raum wird häufig durch die drei Koordinaten eines Punktes des
Starrkörpers in einem Bezugssystem und drei Winkelangaben beschrieben. Die Winkel geben die
Verdrehung der Achsen eines körpereigenen Koordinatensystems, zu den Achsen des ortsfesten
Bezugssystems an, und zwar für den betrachteten Punkt.
Man bezeichnet die drei kartesischen Koordinaten des Punktes P im Bezugssystem auch als
Position des Punktes und die drei Winkelkoordinaten als Orientierung des Punktes des starren
Körpers.
Die Absolutbewegung eines Starrkörpers wird durch vektorielle Überlagerung der Führungsbewegung (Position) und der Relativbewegung (Orientierung) ermittelt. Die einfachste räumliche
Bewegung erfolgt mit drei linearen Achsen, die orthogonal aufeinander stehen. Durch die reine
Translation im Raum verändert sich nur die Position P. Die Bewegung kann mit den Gleichungen
7.5 bis 7.8 berechnet werden.
Mit Linearantrieben oder Laufkränen mit Laufkranbrükke, Laufkrankatze und Laufkranhubwerk
werden diese Bewegungen technisch realisiert.
Der durch keine Bindungen gefesselte starre Körper hat im Raum 6 Freiheitsgrade. Um seine
Lage eindeutig zu beschreiben sind daher 6 Koordinatenangaben erforderlich.
Häufig sind die Bewegungsmöglichkeiten von einer Kette von starren Körpern durch Bindungen
an vorgegebene Bahnen oder durch Fixierung einzelner Punkte der Kette eingeschränkt.
Bei einem aus verschiedenen starren Körpern bestehenden Mehrkörpersystem kann jeder
einzelne Körper solchen Bindungen unterworfen sein, außerdem können sie untereinander
gekoppelt sein. Diese Kopplungen können starr (Gelenke, Stäbe) oder nicht starr (elastische
Federn) sein.
Kopplungen, die nicht starr sind schränken die Anzahl der Freiheitsgrade des Einzelkörpers nicht
ein, es wirken aber über die Kopplungselemente Kräfte zwischen den Körpern, die bei Problemen
in der Kinetik berücksichtigt werden müssen.
Starre Kopplungen (kinematische Kopplungen) schränken die Anzahl der Freiheitsgrade ein, da
zwischen den Koordinaten, die die Lage der Körper beschreiben, feste Beziehungen, sogn.
Zwangsbedingungen, bestehen. Die Anzahl der Koordinaten, die dann mindestens erforderlich
ist, um die Lage eines Systems starrer Körper zu beschreiben, entspricht der Anzahl der Freiheitsgrade des Systems.
Besteht ein Roboterarm aus
α1
einer kinematischen Kette
l3
von Einzelkörpern (Glieder),
l1
α3
die jeweils durch ein Drehgelenk miteinander gekopα2
pelt sind, so hat jeder Einzelkörper aufgrund der Einl2
schränkung der Bewegungsα4
l4
möglichkeit auf eine Rotation nur einen Freiheitsgrad.
l0
y
Roboterarm als
kinematische Kette
P (x, y, z)
mit
5 Freiheitsgraden
x0, y0, z0
α5
x
z
G. Schenke, 3.2003
Automatisierte Antriebe
FB Technik, Abt. E+I
80
x = (l1 + l 2 ⋅ cos α 2 + l 3 ⋅ cos (α 2 + α 3 ) + l 4 ⋅ cos (α 2 + α 3 + α 4 )) ⋅ cosα1
y = l 0 + l 2 ⋅ sin α 2 + l 3 ⋅ sin (α 2 + α 3 ) + l 4 ⋅ sin (α 2 + α 3 + α 4 )
(7.15)
z = (l1 + l 2 ⋅ cos α 2 + l 3 ⋅ cos (α 2 + α 3 ) + l 4 ⋅ cos (α 2 + α 3 + α 4 )) ⋅ sinα1
Abhängig von der Zeit kann ein Punkt P im Raum mit den Koordinaten x, y, z durch den
r
Ortsvektor r (t) beschrieben werden. Da mit dem 5-Achsen-Roboter nur 5 Freiheitsgrade zur
Verfügung stehen, können neben den Raumkoordinaten P(x, y, z) im Arbeitsbereich nur zwei von
drei Orientierungen im Raum erreicht werden. Es sind dieses die Orientierungen α2 + α3 + α4 und
α5.
r
r
Mit den Gl. 7.15 und 7.5 bzw. 7.6 erhält man den Ortsvektor r (t) . Die Geschwindigkeit v (t)
r
erhält man entsprechend Gl. 7.7 und die Beschleunigung a (t) entsprechend Gl. 7.8. Das Antriebsdrehmoment M der jeweiligen Achse muß nach Gl. 7.4 berechnet werden.
Die Berechnung der Drehwinkel α (Lage) und der Winkelgeschwindigkeiten ω (Drehzahl) für die
einzelnen Achsen ist sehr aufwendig. Das Gleichungssystem wird im allg. in Matrizenschreibweise dargestellt und für die jeweiligen Bahnkurven gelöst.
& den Massenträgheitsmomenten J(α), den GeschwindigAus den Winkelbeschleunigungen ω,
keiten ω, den zeitlichen Änderungen der Massenträgheitsmomente dJ(α)/dt und den Widerstandsmomenten MW(α) wird für die Achsen die maximale Antriebsleistung der Servoantriebe
ermittelt.
Bei vielen Robotern wird die notwendige Antriebsleistung im wesentlichen durch die
Beschleunigungsmomente bestimmt.
G. Schenke, 3.2003
Automatisierte Antriebe
FB Technik, Abt. E+I
81