Kinematik in der Mechatronik

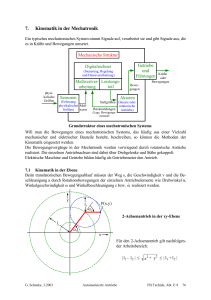
2.
Kinematik in der Mechatronik
Ein typisches mechatronisches System nimmt Signale auf, verarbeitet sie und gibt Signale aus, die
es in Kräfte und Bewegungen umsetzt.
Mechanische Struktur
Getriebe
und
Führungen
Digitalrechner
(Steuerung, Regelung
und Datenverarbeitung)
Meßwertver- Leistungsteil
arbeitung
physikalische
Größen
Sensoren
Kräfte
oder
Bewegungen
Bewegungen
Aktoren
(Erfassung
physikalischer MeßGrößen)
werte
Stellgrößen (lineare oder
rotatorische
Rückmeldungen
Antriebe)
(Lage, Bewegungszustand)
Grundstruktur eines mechatronischen Systems
Will man die Bewegungen eines mechatronischen Systems, das häufig aus einer Vielzahl
mechanischer und elektrischer Bauteile besteht, beschreiben, so können die Methoden der
Kinematik eingesetzt werden.
Die Bewegungsvorgänge in der Mechatronik werden vorwiegend durch rotatorische Antriebe
realisiert. Die einzelnen Antriebsachsen sind dabei über Drehgelenke und Stäbe gekoppelt.
Elektrische Maschine und Getriebe bilden häufig als Getriebemotor den Antrieb.
2.1 Kinematik in der Ebene
Beim translatorischen Bewegungsablauf müssen der Weg s, die Geschwindigkeit v und die Beschleunigung a durch Rotationsbewegungen der einzelnen Antriebselemente wie Drehwinkel ,
Winkelgeschwindigkeit und Winkelbeschleunigung bzw. realisiert werden.
y
P(x,y)
l2
2
2-Achsenantrieb in der xy-Ebene
l1
1
x
Für den 2-Achsenantrieb gilt nachfolgender Arbeitsbereich:
| l1 - l 2 |
G. Schenke, 1.2013
Mechatronik
2
x2 + y
| l1 + l 2 |
FB Technik, Abt. E+I
24
Durch die Geometrie ist der Weg mit seinen xy-Komponenten gegeben.
x = l1 cos
1
+ l 2 cos (
1
+
2)
(2.1)
y = l1 sin 1 + l 2 sin ( 1 + 2 )
Die Geschwindigkeit mit den Komponenten x und y ist die 1. Ableitung des Weges nach der
Zeit.
x =
l1
1
l1
2
1
sin
l2 (
1
1
+
2)
sin (
1
+
2)
(2.2)
y = l1 1 co s 1 l 2 ( 1 + 2 ) co s ( 1 + 2 )
Die Beschleunigung mit den Komponenten x und y ist die 2. Ableitung des Weges nach der
Zeit.
x = l1 1 sin 1 l 2 ( 1 + 2 ) sin ( 1 + 2 )
y = l1
1
co s
co s 1
1
l 2 ( 1 + 2 ) 2 co s ( 1 +
l 2 ( 1 + 2 ) co s ( 1 + 2 )
2)
(2.3)
l1 12 sin 1 l 2 ( 1 + 2 ) 2 sin ( 1 + 2 )
Für die Dimensionierung des Antriebes für jede Achse sind das entsprechende Widerstandsmoment MW ), die Winkelgeschwindigkeit , die Winkelbeschleunigung und das Massenträgheitsmoment J( ) (bezogen auf die jeweilige Achse) erforderlich.
Da das Massenträgheitsmoment J( ) vom Drehwinkel abhängt, ist es während des Bewegungsvorganges auch zeitabhängig.
Das Antriebsdrehmoment M der jeweiligen Achse muss exakt nach Gl. 2.4 berechnet werden.
d
1
dJ( )
M = M W ( ) + J( )
+
(2.4)
dt 2
dt
Das Massenträgheitsmoment J( ) wird mit Hilfe des Steiner´schen Satzes berechnet.
Für die Dimensionierung von Antrieben in der Mechatronik ist häufig nur das größte Antriebsdrehmoment von Interesse. Hieraus können die größten Winkelbeschleunigungen bei maximaler
Nutzlast bzw. abhängig von der Nutzlast berechnet werden.
Im Allgemeinen bestimmen die Beschleunigungsmomente die maximalen Antriebsdrehmomente
in der Mechatronik.
Aus Gl. 2.1 kann zunächst der Drehwinkel 1 und anschließend der Drehwinkel 2 berechnet
werden.
Aus Gl. 2.2 können bei bekannten Drehwinkeln 1 und 2 die Winkelgeschwindigkeiten 1 und
2 berechnet werden.
Für Servoantriebe sind damit die Lage (Drehwinkel ) und die Drehzahl n (Winkelgeschwindigkeit ) bestimmt. Für die maximale Antriebsleistung der Servoantriebe (Dimensionierung des
Servoantriebes) müssen zusätzlich die maximalen Winkelbeschleunigungen 1 und 2 aus Gl.
2.3 ermittelt werden.
2.2 Kinematik im Raum
Im Newton´schen Grundgesetz m a
F präsentiert die Kraft F die Kinetik des Systems, die
Masse m die Trägheit und die Beschleunigung a die Kinematik.
Die Bewegung eines realen Systems ist vollständig beschrieben, wenn der Ortsvektor r (t) für
alle Systemteile bestimmt ist. Für die meisten technischen Systeme muss diese Aufgabe nur
näherungsweise durch Modelle gelöst werden. Das einfachste Modell eines Körpers ist der
Massenpunkt. Die aktuelle Position eines Massenpunktes zu einem Zeitpunkt t ist durch nachfolgenden Ortsvektor gegeben:
r (t) = x(t) e x + y(t) e y + z(t) e z
(2.5)
G. Schenke, 1.2013
Mechatronik
FB Technik, Abt. E+I
25
P (t)
r (t)
y
P (t + t)
r (t)
Bewegung eines Massenpunktes P
in einem kartesischen
Koordinatensystem
r (t + t)
y (t)
ey
ez
0
ex
x
Die aktuelle Position auf der Bahnkurve,
die der Massenpunkt im Raum beschreibt,
ergibt sich zu einem Zeitpunkt t + t als
z
x (t)
der Ortsvektor r (t
t) , der gegenüber
r (t) einen Zuwachs um r (t) aufweist.
Die drei Einheitsvektoren e x , e y und e z stehen senkrecht aufeinander. Das kartesische Koordinatensystem wird als im Raum ruhend oder geradlinig gleichförmig bewegt angenommen.
In einem kartesischen Koordinatensystem (Inertialsystem) sind die Einheitsvektoren von der Zeit
unabhängig, deren Ableitungen nach der Zeit sind gleich Null.
In Matrizenschreibweise gilt für den Ortsvektor r (t) :
z (t)
x(t)
r (t) =
y(t)
(2.6)
z(t)
Durch Ableitung des Ortsvektors r (t) nach der Zeit erhält man die Geschwindigkeit v (t) des
Massenpunktes P auf der Bahnkurve.
x(t)
v(t) = x(t) e x + y(t) e y + z(t) e z =
(2.7)
y(t)
z(t)
Durch Ableitung der Geschwindigkeit v (t) erhält man die Beschleunigung a (t) :
x(t)
a(t) = x(t) e x + y(t) e y + z(t) e z =
(2.8)
y(t)
z(t)
Der Geschwindigkeitsvektor tangiert stets die Bahnkurve und kann auch in einem sog. natürlichen
Koordinatensystem dargestellt werden.
G. Schenke, 1.2013
Mechatronik
FB Technik, Abt. E+I
26
y
s a
t
eb
Bahnkurve
a
r (t + t)
an
ey
ez
r (t)
en
r (t)
Mitbewegtes, natürliches
Koordinatensystem
a
et
0
x
ex
z
Im natürlichen Koordinatensystem ist
ein dem Massenpunkt begleitendes
orthogonales Dreibein mit den Koordinatenachsen t, n und b, die die sog.
Schmiegungsebene festlegen. Hierbei
ist t die Tangentenrichtung in der
Schmiegungsebene, n ist die Normalenrichtung in der Schmiegungsebene und b ist die Binormalenrichtung senkrecht zu t und n.
Im natürlichen Koordinatensystem gilt:
v(t) =
d r (t)
d r ds
=
= et v
dt
ds dt
(2.9)
Dabei ist e t der Tangenteneinheitsvektor. Der Betrag der Geschwindigkeit ist:
|v| = v =
ds
=
dt
2
x 2 + y + z2
v 2x + v 2y + v 2z =
(2.10)
In natürlichen Koordinaten ausgedrückt beträgt die Beschleunigung:
a(t) =
d
dv de t
+
(e t v) = e t
v
dt
dt
dt
(2.11)
Für die Ableitung des Einheitsvektors in Tangentenrichtung nach der Zeit gilt:
de t
de t ds
de t
d
1
=
=
v =
en v =
en v
dt
ds dt
ds
ds
R
(2.12)
Der Beschleunigungsvektor a (t) liegt immer in der Schmiegungsebene. Seine Komponenten in
Tangential- und Normalrichtung heißen Tangential- und Normalbeschleunigung.
a(t) = v e t +
v2
en = a t + a n
R
(2.13)
R ist der Krümmungsradius der Bahnkurve. Die Normalbeschleunigung ist stets zum Krümmungsmittelpunkt M gerichtet, also immer eine Zentripetalbeschleunigung. Für den Betrag der
Beschleunigung gilt:
|a| = a =
a 2x + a 2y + a 2z =
G. Schenke, 1.2013
v
2+
v4 =
R2
a 2t + a 2n
Mechatronik
(2.14)
FB Technik, Abt. E+I
27
Die Bewegung des starren Körpers im Raum kann beschrieben werden, wenn die Lage von zwei
beliebigen Punkten P1 und P2 des starren Körpers verfolgt wird. Die voneinander abhängigen
Ortsvektoren r1 und r2 erfordern sechs Koordinatenangaben.
Die Lage des starren Körpers im Raum wird häufig durch die drei Koordinaten eines Punktes des
Starrkörpers in einem Bezugssystem und drei Winkelangaben beschrieben. Die Winkel geben die
Verdrehung der Achsen eines körpereigenen Koordinatensystems, zu den Achsen des ortsfesten
Bezugssystems an, und zwar für den betrachteten Punkt.
Man bezeichnet die drei kartesischen Koordinaten des Punktes P im Bezugssystem auch als
Position des Punktes und die drei Winkelkoordinaten als Orientierung des Punktes des starren
Körpers.
Die Absolutbewegung eines Starrkörpers wird durch vektorielle Überlagerung der Führungsbewegung (Position) und der Relativbewegung (Orientierung) ermittelt. Die einfachste räumliche
Bewegung erfolgt mit drei linearen Achsen, die orthogonal aufeinander stehen. Durch die reine
Translation im Raum verändert sich nur die Position P. Die Bewegung kann mit den Gleichungen
2.5 bis 2.8 berechnet werden.
Mit Linearantrieben oder Laufkränen mit Laufkranbrücke, Laufkrankatze und Laufkranhubwerk
werden diese Bewegungen technisch realisiert.
Der durch keine Bindungen gefesselte starre Körper hat im Raum 6 Freiheitsgrade. Um seine
Lage eindeutig zu beschreiben sind daher 6 Koordinatenangaben erforderlich.
Häufig sind die Bewegungsmöglichkeiten von einer Kette von starren Körpern durch Bindungen
an vorgegebene Bahnen oder durch Fixierung einzelner Punkte der Kette eingeschränkt.
Bei einem aus verschiedenen starren Körpern bestehenden Mehrkörpersystem kann jeder
einzelne Körper solchen Bindungen unterworfen sein, außerdem können sie untereinander
gekoppelt sein. Diese Kopplungen können starr (Gelenke, Stäbe) oder nicht starr (elastische
Federn) sein.
Kopplungen, die nicht starr sind schränken die Anzahl der Freiheitsgrade des Einzelkörpers nicht
ein, es wirken aber über die Kopplungselemente Kräfte zwischen den Körpern, die bei Problemen
in der Kinetik berücksichtigt werden müssen.
Starre Kopplungen (kinematische Kopplungen) schränken die Anzahl der Freiheitsgrade ein, da
zwischen den Koordinaten, welche die Lage der Körper beschreiben, feste Beziehungen, sog.
Zwangsbedingungen, bestehen. Die Anzahl der Koordinaten, die dann mindestens erforderlich
ist, um die Lage eines Systems starrer Körper zu beschreiben, entspricht der Anzahl der Freiheitsgrade des Systems.
Besteht ein Roboterarm aus
1
einer kinematischen Kette
l3
von Einzelkörpern (Glieder),
l1
die jeweils durch ein Dreh3
gelenk miteinander gekop2
pelt sind, so hat jeder Einzelkörper aufgrund der Einl2
schränkung der Bewegungs4
l4
möglichkeit auf eine Rotation nur einen Freiheitsgrad.
l0
y
Roboterarm als
kinematische Kette
P (x, y, z)
mit
5 Freiheitsgraden
x0, y0, z0
x
5
z
G. Schenke, 1.2013
Mechatronik
FB Technik, Abt. E+I
28
x = (l1
l 2 cos
y = l0
l 2 sin
2
2
+ l 3 cos (
+ l 3 sin (
2
2
+
+
3)
3)
l 4 cos (
l 4 sin (
2
2
+
+
3
3
4 ))
4)
cos
1
(2.15)
z (l1 l 2 cos 2 + l 3 cos ( 2 + 3 ) l 4 cos ( 2 + 3
4 )) sin 1
Abhängig von der Zeit kann ein Punkt P im Raum mit den Koordinaten x, y, z durch den
Ortsvektor r (t) beschrieben werden. Da mit dem 5-Achsen-Roboter nur 5 Freiheitsgrade zur
Verfügung stehen, können neben den Raumkoordinaten P(x, y, z) im Arbeitsbereich nur zwei von
drei Orientierungen im Raum erreicht werden. Es sind dieses die Orientierungen 2 + 3 + 4 und
5.
Mit den Gl. 2.15 und 2.5 bzw. 2.6 erhält man den Ortsvektor. Die Geschwindigkeit v (t) erhält
man entsprechend Gl. 2.7 und die Beschleunigung a (t) entsprechend Gl. 2.8. Das Antriebsdrehmoment M der jeweiligen Achse muss nach Gl. 2.4 berechnet werden.
Die Berechnung der Drehwinkel (Lage) und der Winkelgeschwindigkeiten (Drehzahl) für die
einzelnen Achsen ist sehr aufwendig. Das Gleichungssystem wird im allg. in Matrizenschreibweise dargestellt und für die jeweiligen Bahnkurven gelöst.
Aus den Winkelbeschleunigungen , den Massenträgheitsmomenten J( ), den Geschwindigkeiten , den zeitlichen Änderungen der Massenträgheitsmomente dJ( )/dt und den Widerstandsmomenten MW ) wird für die Achsen die maximale Antriebsleistung der Servoantriebe
ermittelt.
Bei vielen Robotern wird die notwendige Antriebsleistung im wesentlichen durch die
Beschleunigungsmomente bestimmt.
G. Schenke, 1.2013
Mechatronik
FB Technik, Abt. E+I
29