Ökonomie am 2.11.2005 - Webarchiv ETHZ / Webarchive ETH

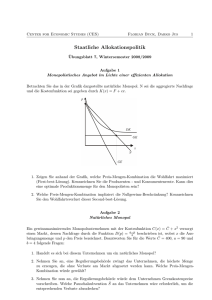
Ökonomie am 17.10.2012
Analyse von Märkten: Teil I
Vortrag: Die Schweiz in der Welt –
Chancen, Risiken, neue Konstellationen
 Bundesrat Johann SchneiderAmmann (Eidgenössisches
Volkswirtschaftsdepartement)
spricht zur globalen Finanz- und
Wirtschaftskrise und den
Handlungsoptionen der Schweiz
 22. Oktober 2012, 18.00h
 Universität Zürich, KOH-B-10
2
Hausaufgabe vom 03.10.2012
1. a) Nach einem Milchpreisanstieg von 2,00 Fr auf 2,50 Fr erhöht sich
die Milchproduktion von 80‘000l auf 120‘000l. Berechnen Sie die
Preiselastizität des Angebots und interpretieren Sie das Ergebnis.


Die Preiselastizität des Angebots, 𝜀𝑥𝐴 , gibt an, um wie viel Prozent
die angebotene Menge steigt oder sinkt, wenn der Preis um 1% steigt
oder sinkt.
In diesem Fall berechnet sich die Preiselastizität wie folgt:
𝜀𝑥𝐴

∆𝑥 𝐴 𝑝
120 000 − 80 000
2
=
∙
=
∙
=2
∆𝑝 𝑥 𝐴
2.5 − 2
80 000
Interpretation: Bei einer Preissteigerung von 1% steigt das Angebot um
2%. Da das Angebot stärker steigt als der Preis, ist das Angebot
elastisch.
3
Hausaufgabe vom 03.10.2012
b) Zeichnen und interpretieren Sie eine völlig elastische und eine
völlig unelastische Preiselastizität des Angebots.
(a) Völlig unelastisches Angebot
(b) Völlig elastisches Angebot
4
Hausaufgabe vom 03.10.2012
2. Lückentext: Vervollständigen Sie die Sätze mit der passenden
Kostenart.
a) Die Durchschnittskosten sinken, wenn Grenzkosten niedriger sind,
und steigen, wenn die Grenzkosten höher sind.
b) Kosten, die unabhängig von der produzierten Menge anfallen sind
Fixkosten.
c) In der kurzen Frist beinhalten die variablen Kosten der
Eiscremeproduktion die Kosten für Zucker und Sahne, aber
nicht die Kosten der Produktionsstätten.
d) Der Gewinn ist die Differenz zwischen Umsatz und Kosten
(Gesamtkosten).
e) Die Kosten zur Produktion eines weiteren Gutes sind die Grenzkosten.
5
Hausaufgabe vom 03.10.2012
3. Nehmen Sie an, dass die aggregierte Kostenfunktion aller
Unternehmen auf dem Markt für Ökonomielehrbücher durch
𝐊 𝐱 = 𝟐𝐱 𝟐 + 𝟓𝐱 + 𝟐𝟓 gegeben ist. Wie sieht dann die
Angebotsfunktion aus?

Bei vollständiger Konkurrenz gilt: Angebotskurve = Grenzkostenkurve
(ansteigender Teil)

Die Grenzkosten/das Angebot sind hier gegeben durch: 𝐾 ′ 𝑥 = 4𝑥 + 5
6
Hausaufgabe vom 03.10.2012
4. Nehmen Sie nun ausserdem an, dass der Marktpreis von
Ökonomielehrbüchern bei CHF 25 liegt. Wie viele Bücher werden dann
auf dem Markt angeboten und wie hoch ist der Gewinn aller
Unternehmen?

Bei vollständiger Konkurrenz gilt Grenzkosten=Preis: K‘(x) = p
Also 4x+5 = 25 → x = 5

Zum Preis von 25 CHF werden 5 Ökonomiebücher am Markt angeboten

Der Gewinn berechnet sich wie folgt:
𝐆 𝐱 = 𝐄 𝐱 − 𝐊 𝒙 = 𝟐𝟓𝐱 − 𝟐𝒙𝟐 − 𝟓𝐱 − 𝟐𝟓 → 𝐆 𝟓 = 𝟐𝟓

𝐆′ (𝟓) = 𝟎 und 𝐆′′ 𝟓 = −𝟒 < 𝟎 → Die notwendige und hinreichende
Bedingung für ein Gewinnmaximum bei x = 5 sind somit erfüllt.
7
Hausaufgabe vom 03.10.2012
8
9
Lernziele
 Sie kennen den Zusammenhang zwischen individuellen
Angebots- und Nachfragekurven und den MarktAngebots- und Nachfragekurven
 Sie wissen, wie die Preisbildung bei vollkommener
Konkurrenz funktioniert und können die verschiedenen
ökonomischen Renten bei vollkommener Konkurrenz
bestimmen
 Sie wissen, wie die Preisbildung im Monopol funktioniert
und welche Renten im Monopol entstehen
 Sie wissen, was ‘natürliche Monopole’ sind
10
Aggregation von Angebot und
Nachfrage

Bisher: Nachfragekurven einzelner Haushalte
und Angebotskurven einzelner Unternehmen

Jetzt: Zusammenfassung („Aggregation“) zu
Markt-Nachfrage- bzw. Angebotskurven

Prinzip dabei: Horizontaladdition
11
Aggregation von Angebot und
Nachfrage
12
Interpretation: Aggregierte
Angebotsfunktion
Bei vollständigem Wettbewerb gilt:
 Die Angebotsfunktion der einzelnen
Unternehmen entspricht bei vollständigem
Wettbewerb ihren Grenzkosten
 Die aggregierte Angebotsfunktion entspricht
bei vollständigem Wettbewerb somit den
gesamtgesellschaftlichen Grenzkosten für
die Herstellung des Gutes
13
Interpretation: Aggregierte
Nachfragefunktion
Analog gilt für die Nachfrageseite:
 Die Nachfragefunktion der einzelnen
Haushalte entspricht bei vollständigem
Wettbewerb ihren Grenznutzen
 Die aggregierte Nachfragefunktion
entspricht bei vollständigem Wettbewerb
somit den gesamtgesellschaftlichen
Grenznutzen eines Gutes
14
Preisbildung bei vollkommener
Konkurrenz

Basis: Im Wettbewerb gibt es viele kleine
Nachfrager und Anbieter

Marktgleichgewicht: Marktpreis hat
denjenigen Wert, bei dem angebotene und
nachgefragte Menge gleich gross sind

Bei Markt-Ungleichgewicht gibt es eine
Tendenz zurück zum Gleichgewicht
15
Preisbildung bei vollkommener
Konkurrenz
16
Aufgaben für Gruppenarbeit - A
Marktforscher haben für ein bestimmtes Gut die
folgende Nachfragefunktion ermittelt:
xN = 1‘600 – 300p. Die Angebotsfunktion lautet:
xA = 1‘400 + 700p. Berechnen Sie den Gleichgewichtspreis und die Gleichgewichtsmenge im
Wettbewerb!
Antwortmöglichkeiten:
A: p* = 0,2 und x* = 700
B: p* = 3,0 und x* = 700
C: p* = 0,2 und x* = 1540
D: p* = 3,0 und x* = 1540
17
18
„Effizienz“ bei vollkommener
Konkurrenz

Bei vollständigem Wettbewerb gilt:
Grenznutzen (Nachfrage)= Grenzkosten (Angebot)

Die notwendige Bedingung für ein soziales
Optimum (Pareto-Optimum) ist also bei
vollständigem Wettbewerb erfüllt:
max U(x) – K(x)  U‘(x) = K‘(x)

Dies ist bei eingeschränktem Wettbewerb,
zum Beispiel beim Monopol, nicht der Fall
19
Effizienz und Wohlfahrtsmaximum
bei vollkommener Konkurrenz


Pareto-Effizienz: (s. Kapitel 3, K-N-A)
Eine Güterverteilung ist effizient, wenn jede
andere Verteilung mindestens ein Individuum
schlechter stellen würde. Der Nettonutzen für
die Gesellschaft ist maximal
Potentielle Pareto-Effizienz:
Die besser Gestellten können die schlechter
Gestellten aus ihrem Gewinn kompensieren
20
Ökonomische Renten vollkommener
Konkurrenz: Konsumentenrente

Konzept: KR ist die nicht ausgeschöpfte
Zahlungsbereitschaft der Konsumenten
21
Ökonomische Renten vollkommener
Konkurrenz: Produzentenrente

Konzept: PR ist die Differenz zwischen Erlös
und (variablen) Kosten
22
Wohlfahrtsmaximum:
 Die Wohlfahrt
(Summe der
Konsumenten und
Produzentenrente)
ist maximal
 Keine ParetoVerbesserung
möglich
23
Welche Aussage ist falsch?
Eine potentielle Pareto-Verbesserung liegt vor,
wenn durch eine neue Verteilung
A) Die Konsumentenrente sinkt, die Produzentenrente in gleichem
Umfang oder stärker steigt
B) Die Produzentenrente sinkt, die Konsumentenrente in gleichem
Umfang oder stärker steigt
C) Die Konsumentenrente steigt, ohne dass die Produzentenrente
sinkt
D) Die Produzentenrente steigt, ohne dass die Konsumentenrente
sinkt
E) Die Summe aus Produzenten- und Konsumentenrente sinkt
24
25
Monopol

Gründe für Monopol:
Schlüsselressource im Besitz einer
Firma (Diamanten)/ Staatliche
Regulierung (staatlicher Auftrag oder
Patente bzw. Urheberschutz)/
Kostenstruktur der Industrie
(„natürliches Monopol“)
26
Monopol





Auch hier Annahme der Gewinnmaximierung
Aber: Preis ist kein Datum mehr!
Folglich: E(x) = p(x) ∙ x
Und: E‘(x) = x ∙ p‘(x) + p(x) ∙ 1 („Produktregel“)
Also: x p‘(x) + p(x) = K‘(x) für Gmax
27
Monopol


Beispiel: p(x) = b – ax
=> E(x) = p(x) x = bx - ax²
=> E’(x) = b – 2ax
=> b – 2ax = K’(x)
Dies ist die notwendige Bedingung für
Gmax
28
Monopol





Hinreichende Bedingung für Gmax:
=> in allgemeiner Form G’’(x) <0
Es ist: G’’(x) = E’’(x) – K’’(x)
Also: E’’(x) < K’’(x)
Im Beispiel: E’(x) = b – 2ax
E’’(x) = -2a
Also: -2a < K’’(x)
29
Preisbildung beim Monopol
30
Preisbildung beim Monopol

Der Monopolist bietet im Cournot-Punkt an
(GK = GE)

Der Preis im Monopol ist höher, die Menge
kleiner als bei vollkommener Konkurrenz

Dies dient häufig der Kritik am Monopol
31
Ökonomische Renten: Vergleich
Konkurrenz - Monopol
32
Ökonomische Renten: Vergleich
Konkurrenz - Monopol

Fazit 1: Monopol bringt Umverteilung
von Konsumentenrente zu
Produzentenrente mit sich (Fläche A)

Fazit 2: Monopol bedeutet
Wohlfahrtsverlust; Teile der Renten
fallen weg (Fläche C und D)
33
Richtig oder Falsch?

Die Umverteilung der Konsumentenrente zur Produzentenrente stellt aus
volkswirtschaftlicher Sicht ein Problem
dar.
Richtig (T) oder Falsch (F)?
34
Preisbildung beim Monopol

Argument zugunsten von Monopol: Die
Aussicht auf (vorübergehende) Monopolgewinne gibt Anreiz zur Innovation

Lizenzen, Patente zur Sicherung der
Amortisation von Forschungs- und
Entwicklungskosten

Wichtig aber: Befristung dieser Gewinn“Garantie“
35
Natürliches Monopol

Definition eines natürlichen Monopols:
„Eine Marktsituation, in der ein einzelnes
Unternehmen die Marktnachfrage besser bedienen
kann, als eine Gruppe aus mehreren Unternehmen“

Beispiele für natürliche Monopole:
–
–
–
–
Schienennetz
Stromnetz
Gas-Pipelines
Post
36
Natürliches Monopol

Charakteristika:
– Hohe Fixkosten
– Niedrige Grenzkosten
– Durchschnittskosten (DK) im Bereich der
Nachfrage grösser als die Grenzkosten (GK)
→ Wettbewerb führt zu Verlusten bei den
Unternehmen, da p=GK<DK
→ keine Bereitstellung des Gutes
37
Natürliches Monopol

Monopolist könnte das Gut produzieren, aber:
 Hoher Monopolpreis p>DK
 Wohlfahrtsverlust

Lösung:
 Staat produziert das Gut und bietet zu Durchschnittskosten an,
p=DK
 Monopolist produziert das Gut und muss das Gut zu p=DK anbieten
→ Erfordert staatlichen Markteingriff in Form eines Höchstpreises
38
39
Hausaufgaben für 24.10.2012
1. Ein Monopolbetrieb ist durch einen Erlös von
E(x) = -x(x-60) und Gesamtkosten
K(x) = 30x + 100 gekennzeichnet. Bei
welcher Stückzahl erreicht der Betrieb den
grössten Gewinn? Bei welchen fixen Kosten
würde er im Gewinnmaximum weder mit
Gewinn noch mit Verlust arbeiten?
40
Hausaufgaben für 24.10.2012
2. Henry, Bea und Romy betreiben die einzige
Kneipe in einer Stadt. H will so viele Drinks
wie möglich ohne Verlust verkaufen. B
möchte so viel Erlös wie möglich erzielen. R
möchte den maximalen Profit realisieren.
Welche Preis-Mengen-Kombinationen
entsprechen diesen drei Strategien?
Erläutern und begründen Sie Ihre Antworten
anhand von Grafiken.
41
Hausaufgaben für 24.10.2012
3. Ein Pharmaunternehmen hat ein neues
Medikament entwickelt. Das Unternehmen hat ein
Patent auf dieses Medikament bekommen und ist
daher einziger Anbieter dieses Medikaments. Die
Herstellungskosten sind gegeben durch K(x)=20x.
Das Unternehmen nimmt folgende Nachfragefunktion an: x=100-1/2 p.
Berechnen Sie den Preis und die angebotene
Menge im Gleichgewicht.
42
Hausaufgaben für 24.10.2012
4.
a.
b.
Die Firma SAP entwickelt einen neuen Chip, auf
den sie sofort ein Patent erhält.
Zeichnen Sie ein Diagramm, das
Produzentenrente, Konsumentenrente und
Gesamtrente für den Markt des neuen Chips zeigt
Wie ändern sich die Grössen aus a., wenn SAP
vollständige Preisdifferenzierung machen kann,
d.h. die unterschiedliche Zahlungsbereitschaft der
Nachfrager adäquat berücksichtigt?
43
Hausaufgaben für 24.10.2012
5. Bereiten Sie Kapitel 4 (speziell Kap. 4.3
und 4.4) im Skript vor
 wird nächste Woche weiter besprochen
44