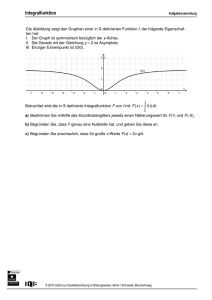
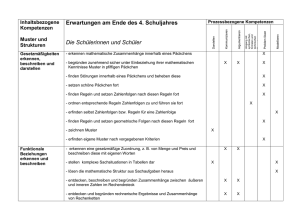
2 3√x

Fakultät für Mathematik
Campus Essen
Wieland Wilzek
22.8.-2.9.2016
Aufgabensammlung: Vertiefung der Schulmathematik
1.1
Handelt es sich bei den folgenden Zuordnungen um Funktionen? Begründen Sie ihre
Entscheidung.
a) Person → Körpergröße
b) Körpergröße → Person
c) x∈ℝ → y∈ℝ mit y 2=x
d) x∈ℝ → y 2
e) x∈ℝ → x
f) Sei f (x ) eine beliebige Funktion.
x∈ℝ → f ( f ( x ))
1.2
Versuchen Sie die folgenden Behauptungen zu begründen oder zu widerlegen.
a) Die Funktion, die jedem positivem x-Wert die 1 und jedem negativem x-Wert die Null
zuordnet, ist stetig.
b) Die Funktion, die jedem x-Wert ihren Betrag zuordnet, ist stetig.
c) Sei a∈ℝ und f (x ) eine stetige Funktion, dann ist a⋅ f (x ) auch eine stetige
Funktion.
d) Sei f ( x ) eine stetige Funktionen und g ( x) eine beliebige weitere Funktion, dann ist
auch f (x )+g ( x) eine stetige Funktion.
1.3
Wir betrachten die Funktion f (x )=x 2+1 . Berechnen Sie...
a) die Ableitung von f an der Stelle 2,
b) die Sekantensteigung im Intervall [1 ; 2] ,
c) und die Sekantensteigung im Intervall [1 ; 3] .
d) Hat Sie etwas verwundert? Wenn ja, warum? Könnte man die Ableitung nicht auch wie
folgt definieren?
f ( x 0+h)− f ( x 0−h)
f ' ( x)=lim
2h
h→0
e) Versuchen Sie diesen Ausdruck graphisch darzustellen.
2.1
Berechnen Sie die folgenden Ableitungen.
a) f (x )=2x 3−4x+9 b) f ( x )=−2 e x +3cos( x) c) f (x )=sin ( x 2−1)
d) f (x )=sin ( x)ln ( x) e) f ( x )=e x⋅cos( x) f) f (x )=tan( x )
3x 2
g) f (x )= 3
h) f (x )=xe x−4xe x +3xe x
2√x
2.2
Leiten Sie die Quotientenregel (
f ( x)
)' =? mithilfe der Produkt- und Kettenregel her.
g ( x)
2.3
Leiten Sie zweimal ab.
a) f (x )=x−
1
2 √ x+x
x 2−4
b) f ( x )= 2 c) f (x )=
d) f (x )=x−1 ( x+ x−3)
x
√x
x
2.4
Überprüfen Sie folgende Behauptungen für die Funktionen f und g.
a) Ist x 0 eine Nullstelle der Funktion g, dann ist x 0 auch eine Nullstelle der Funktion
f (g ( x)) .
b) Wenn die Funktion f eine Nullstelle hat, dann hat auch die Funktion f (g ( x)) eine
Nullstelle.
c) Hat der Graph von g eine waagerechte Tangente, so gilt dies auch für den Graphen von
f (g ( x)) .
3.1
a) Geben sie eine nicht zu einfache Funktion an, die zur Y-Achse symmetrisch ist.
b) Geben sie eine nicht zu einfache Funktion an, die zum Ursprung symmetrisch ist.
c) Gibt es Funktionen, die zur x-Achse symmetrisch sind?
1
d) Untersuchen Sie die Funktion f ( x )=sin( x− ) auf besondere Symmetrien.
x
e) Geben sie ein Kriterium an, mit dem man untersuchen kann, ob eine Funktion zu der
Geraden x=a symmetrisch ist.
3.2
Entscheiden sie, ob g dieselben Extremstellen und Extremwerte hat wie die Funktion f.
Begründen Sie ihre Entscheidung.
a) g ( x)= f ( x)+3
b) g ( x)=2⋅ f ( x ) c) g ( x)= f ( x−5)
3.3
Mit einem 100m langen Zaun soll ein möglichst großes
Rechteck abgesteckt werden. In den Fällen B und C
werden dabei noch vorhandene Mauern ausgenutzt.
Berechnen Sie die idealen Maße und den Flächeninhalt
a) mithilfe der Differentialrechnung und
b) mithilfe der quadratischen Ergänzung.
3.4
Diskutieren Sie die folgenden Funktionen:
a) f (x )=−x 3+6x 2
b) f (x )=( 2−x)e x
4.1
Berechnen Sie die folgenden Integrale:
a)
e)
∫ 2x2−3x+7 dx b) ∫ 3 e x dx c) ∫(2sin( x)−4cos (x ))dx
3
Π/ 2
Π
x 3−2x 2
3
dx
(sin(
x))
dx
f)
g)
∫ x
∫ −3 cos(2x)dx
∫
−Π
d)
∫ e x+2 dx
Π/ 4
−2
4.2
Versuchen Sie die folgenden Behauptungen zu begründen oder zu widerlegen.
a) Falls eine Funktion f auf ganz ℝ eine Stammfunktion besitzt, dann auch eine, deren
Graph durch den Ursprung geht.
b) Bildet man eine Stammfunktion von einer Funktion f und dann wieder eine
Stammfunktion, usw... erhält man nie wieder die Funktion f.
2
1
1
−1 2
] =−1<0 .
c) Obwohl 2 >0 für x≠0 , gilt ∫ 2 dx=[
x −2
x
−2 x
d) Sind die Funktionen f und g auf dem Intervall [a;b] stetig und ist f (x )≤g ( x) für alle x
b
aus [a;b], so gilt auch
b
∫ f ( x )dx≤∫ g ( x) dx
a
.
a
e) Sind M und m das Maximum bzw. das Minimum von f auf [a;b], so gilt
b
m(b−a )≤∫ f ( x ) dx≤M (b−a) .
a
4.3
Entscheiden Sie ohne Rechnung, ob das Integral positiv, negativ oder null ist.
4
1
1 2
a) ∫ −x +1 dx b) ∫ x −1 dx c)
0
−2 4
2
1
∫x
−1
20
3
dx d)
∫ √ x dx
0
4.4
Ist die Funktion f auf dem Intervall [a;b] stetig, so entsteht bei Rotation der Fläche
zwischen dem Graphen von f und der x-Achse über [a,b] ein Körper mit dem Volumen
b
2
V =Π⋅∫ ( f ( x )) dx .
a
a) Wie hängt diese Formel mit der Herleitung des Integrals und der Formel für den
Flächeninhalt des Kreises zusammen?
b) Leiten sie mit Hilfe dieser Formel die Volumenformeln für Zylinder, Kegel und Kugeln
her.
5.1
Weisen Sie nach, dass es sich bei der folgenden Struktur um einen Vektorraum handelt.
x1 x2
x x2
a x1 a x2
∈ℝ2x2 . Wir definieren: a⋅ 1
=
Sei a∈ℝ und
und
x3 x4
x3 x4
a x3 a x4
( )
( )( )(
x1
x3
x2
y
+ 1
x4
y3
y2
x +y
= 1 1
y4
x 3+ y3
( )(
x 2+ y 2
x 4+ y 4
)
)
5.2
Versuchen Sie die folgenden Behauptungen zu begründen oder zu widerlegen.
a) Sei a∈ℝ und v ∈ℝ3 , dann sind die zu a⋅v zugehörigen Pfeile um das ∣a∣ -fache
länger als die zu v zugehörigen Pfeile.
b) Verschiebt man einen Punkt A um einen Vektor v und den so erhaltenen Punkt B wieder
um einen Vektor w auf einen Punkt C, so ist jeweils der Pfeil ⃗
AB und der Pfeil ⃗
BC
⃗
höchstens so lang wie der Pfeil AC .
c) Seien A,B,C, v und w wie bei b). Dann ist die Summe der Pfeillängen zu v und w immer
größer oder gleich der Pfeillänge von ⃗
AC .
5.3
Eine quadratische Matrix heißt magisches Quadrat, wenn die Summen der Zahlen in jeder
0 1 2
2 9 4
Spalte, jeder Zeile und jeder Diagonale gleich sind. z.B.: 3 1 −1 oder 7 5 3 .
0 1 2
6 1 8
Wenn eine Vektorraumstruktur wie in 5.1 definiert wird, ist klar, dass die Rechengesetze,
die für alle Matrizen und Skalare gelten auch für diese speziellen Matrizen gelten. Um
festzustellen, ob die Menge aller magischer Quadrate ebenfalls ein Vektorraum ist, muss
nur also noch geprüft werden, ob die Summe zweier magischer Quadrate und eine skalare
Multiplikation mit einem magischen Quadrat wieder ein magisches Quadrat ergeben.
Überprüfen Sie das.
(
) ( )
6.1
Lösen Sie das folgende LGS:
1 −2 7 0 x 1
−10
4 2
3 1 x2
⋅
= 5
0 6 −6 6 x 3
18
1 0
0 2 x4
1
(
)( ) ( )
Vergleichen Sie auch ihr Vorgehen mit anderen. An welchen Stellen weichen Sie von dem
genauen Vorgehen des Gauß-Algorithmus ab? Was ist wohl der geschickteste Weg?
6.2
Schreiben Sie einen Algorithmus (allgemeine Anleitung) zu folgenden Verfahren auf:
(Zahlenbeispiele können helfen, die Beschreibung muss aber so sein, dass jemand, der
das Verfahren nicht kennt, es für beliebige Zahlen durchführen kann.)
a) Auflösen nach x einer Gleichung der Form ax+by +cx+dy+…=ex + fy+… . Dabei
stehen a,b,c … für feste Zahlen aus ℝ und y ist eine weitere Variable.
b) Bestimmen der Nullstellen einer Gleichung der Form ax 2+bx+c=d . Machen Sie eine
Fallunterscheidung für spezielle Fälle wie b=0 .
6.3
( )
1 2 ⃗x
a) Welche Punkte werden durch die Abbildung f (⃗x )=
auf den Ursprung
2 4
abgebildet?
a b ⃗x
b) Begründen Sie: Wenn eine durch eine Abbildungsvorschrift f (⃗x )=
gegebene
c d
Abbildung zwei verschiedene Punkte auf den gleichen Punkt abbildet, dann bildet sie
mindestens einen vom Ursprung verschiedenen Punkt auf den Ursprung ab.
c) Begründen Sie: Wenn ein vom Ursprung verschiedener Punkt P von der in b)
beschriebenen Abbildung auf den Ursprung abgebildet wird, so werden unendlich viele
Punkte auf den Ursprung abgebildet.
d) Affine Abbildungen werden im Allgemeinen durch die Form f (⃗x )=M ⃗x +⃗
b mit einer
n
beliebigen nxn-Matrix M und einen Vektor b des ℝ angeben. Was passiert für den
Spezialfall n=1?
( )
6.4
Es sollen zwei zweistellige Zahlen mit gleicher Quersumme gefunden werden, von denen
die eine doppelt so groß wie die andere ist. Finden Sie möglichst alle Zahlen. Hilft hier das
Aufstellen eines LGS weiter?
7.1
a) Zeichnen Sie die Gerade, welche durch die Parameterform
( xy)=(12)+t (−2
−1 )
gegeben
ist.
b) Bestimmen sie Koordinatenform von
( xy)=(ab)+t ( dc ) . Fällt ihnen etwas auf?
c) Setzen Sie die Werte aus a) in die Koordinatenform, die Sie in b) bestimmt haben, ein.
Fällt ihnen jetzt etwas auf?
d) Leiten Sie aus der Koordinatenform −x− y=3 eine Parametergleichung her.
7.2
Beantworten und begründen Sie:
a) Welche Bedingung muss ein Punkt und eine Gerade erfüllen, damit sie eine Ebene
eindeutig festlegen?
b) Legen zwei sich schneidende Geraden eine Ebene eindeutig fest?
c) Legen zwei parallele Geraden eine Ebene eindeutig fest?
d) Legen zwei windschiefe Geraden eine Ebene eindeutig fest?
e) In welchen Fällen gilt für Vektoren die Gleichung ∣⃗
a +⃗b∣=∣⃗
a∣+∣⃗
b∣ ?
f) Gilt das Distributivgesetz bei dem Skalarprodukt und der Vektoraddition?
7.3
Welche besondere Lage haben die Ebenen?
a) E : x 1=0 b) E : x 2=0 c) E : x 3=0 d) E : x 1=−7
7.4
Sei f (x )= y eine stetige Funktion, die von ℝ nach ℝ abbildet.
a) Wie könnte man den Graphen der Funktion als „mathematisches Objekt“ beschreiben?
b) Gibt es zu jeder Funktion f genau einen Graphen?
c) Gibt es zu jedem „zusammenhängenden“ Graphen genau eine Funktion f? Wie sollte
man Gleichheit bei Funktionen definieren?
8.1
a) Wie könnte sich eine Klasse mit 30 Kindern zusammensetzen, in der die meisten
Jungen Fußball spielen, aber die die meisten FußballspielerInnen Mädchen sind?
b) A bedeutet „Junge“, B „FußballspielerIn“. Berechnen Sie P A( B) , P (B) , P B (A) und
P ( A) .
8.2
Bei einem Glücksspiel zieht man 3 Kugeln ohne Zurücklegen aus einer Urne, die vier rote,
drei blaue und zwei grüne Kugeln enthält. Ein Spiel kostet 3 Euro. Für jede rote Kugel, die
man zieht, gewinnt man 2 Euro.
a) Wie hoch ist die Wahrscheinlichkeit drei rote Kugeln zu ziehen?
b) Wie hoch ist der Erwartungswert? Machen die Betreiber des Glücksspiels auf lange
Sicht Gewinn?
c) Kann es sein, dass jemand das Spiel dreimal hintereinander spielt und jedes Mal drei
blaue Kugeln zieht?
8.3
Versuchen Sie die folgenden Behauptungen zu begründen oder zu widerlegen.
a) Jedes Zufallsexperiment hat einen Erwartungswert.
b) Bei symmetrischen Wahrscheinlichkeitsverteilungen liegt der Erwartungswert in der
Mitte.
c) Wenn die Ereignisse E 1 und E 2 stochastisch unabhängig sind und die Ereignisse
E 2 und E 3 stochastisch unabhängig sind, dann sind auch die Ereignisse E 1 und
E 3 stochastisch unabhängig.
d) Wenn die Ereignisse E 1 und E 2 stochastisch unabhängig sind, so ist auch E 1 und
das Gegenereignis zu E 2 stochastisch unabhängig.
8.4
Eine Münze wird so lange geworfen, bis eine Seite zum zweiten Mal erscheint. Bestimmen
Sie die Wahrscheinlichkeitsverteilung für die Anzahl der Würfe sowie den Erwartungswert.
9.1
Bei einem Test gibt es acht Fragen mit jeweils drei Antworten, von denen nur eine richtig
ist. Eine Versuchsperson kreuzt bei jeder Frage rein zufällig eine Antwort an. Mit welcher
Wahrscheinlichkeit hat sie
a) genau vier richtige Antworten,
c) höchstens drei richtige Antworten?
b) weniger als drei richtige Antworten,
9.2
Begründen Sie die folgenden Aussagen:
a) Obwohl Binomialkoeffizienten als Brüche berechnet werden, sind sie immer ganzzahlig.
n + n = n+1
n = n
b) Es gelten die Beziehungen
und
.
k
n−k
k
k +1
k +1
n =1
n =1
c) Es gilt
und
(Wie ist dann scheinbar die Fakultät von Null definiert?).
n
0
d) Es gibt einen Zusammenhang zwischen binomischen Formeln und dem
Binomialkoeffizienten.
3
2
3 3 3 a 2 b+ 3 ab2+ 3 b 3
2 a 2+ 2 ab+ 2 b 2
z.B. gilt: (a+b) =
oder (a+b) = a +
.
3
2
1
0
2
1
0
(*Begründen Sie auch, warum dieser Zusammenhang für höhere Potenzen besteht.)
()( )( )
()( )
()
()
() () () ()
() () ()
9.3
(
)
0,6 0
.
0,4 1
a) Zeichnen Sie ein Prozessdiagramm.
b) Wie sieht die Verteilung nach einem Zyklus aus, wenn sich zu Beginn je 100 Einheiten
in beiden Zuständen befinden?
c) Wie entwickelt sich diese Verteilung wohl auf lange Sicht?
d) Fällt Ihnen eine Situation ein, worauf dieser Prozess passen könnte?
Gegeben sei die Übergangsmatrix
9.4
Begründen Sie die folgenden Aussagen:
a) Zu der Matrix
( )
0 1
1 0
gibt es zwar eine stabile Verteilung. Jedoch existiert keine
Grenzmatrix.
b) Das Produkt zweier stochastischer 2x2-Matrizen ist wieder eine stochastische Matrix.
a
b
Tipp: eine allgemeine stochastische Matrix im 2x2-Fall hat die Gestalt
.
1−a 1−b
(
)