4.4.3. Magnetische Flußdichte und Kraftwirkungen im Magnetfeld

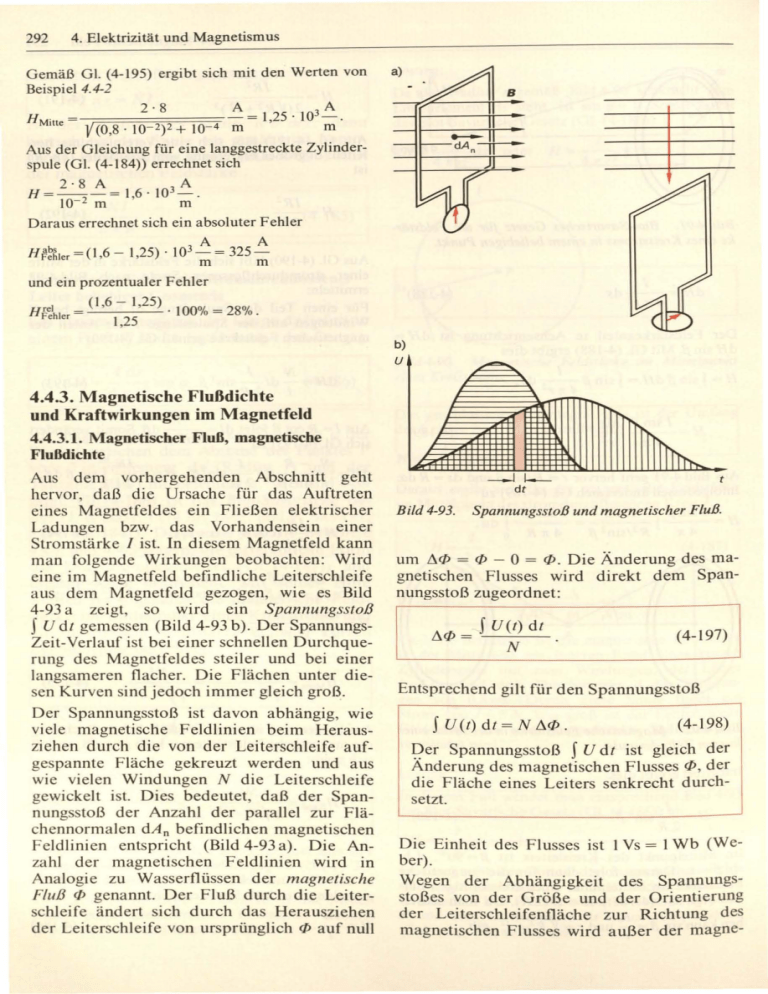
292
4. Elektrizität und Magnetismus
Gemäß GI. (4-195) ergibt sich mit den Werten von
Beispiel 4.4-2
2.8
A = 1,25 .
V(0 ,8 ,10- 2)2 + 10 4m
a)
W ~.
m
Aus der Gleichung für eine langgestreckte Zylinderspule (GI. (4-184)) errechnet sich
2· 8 A
A
H = - 2- = 1,6 ' 10 3 -
.
10- m
m
Daraus errechnet sich ein absoluter Fehler
3
A
A
m
m
H ~~ler =( 1 ,6 - 1,25)' 10 - = 325-
und ein prozentualer Fehler
rel
H Fehler
= ( 1,6 - 1,25) . 10001 = 2801
/0
/0 •
1,25
b)
U
4.4.3. Magnetische Flußdichte
und Kraftwirkungen im Magnetfeld
4.4.3.1. Magnetischer Fluß, magnetische
Flußdichte
Aus dem vorhergehenden Abschnitt geht
hervor, daß die Ursache für das Auftreten
eines Magnetfeldes ein Fließen elektrischer
Ladungen bzw. das Vorhandensein einer
Stromstärke I ist. In diesem Magnetfeld kann
man fol gende Wirkungen beobachten: Wird
eine im Magnetfeld befindliche Leiterschleife
aus dem Magnetfeld gezogen, wie es Bild
4-93 a zeigt, so wird ein Spannungssloß
U dl gemessen (Bild 4-93 b) . Der SpannungsZeit-Verl a uf ist bei einer schnellen Durchquerung des Magnetfeldes steiler und bei einer
la ngsa meren flacher. Die Flächen unter diesen Kurven sind jedoch immer gleich groß.
J
Der Spannungsstoß ist davon abhängig, wie
viele magnetische Feldlinien beim Herausziehen durch die von der Leiterschleife aufgespannte Fläche gekreuzt werden und aus
wie vielen Windungen N die Leiterschleife
gewickelt ist. Dies bedeutet, daß der Spannungsstoß der Anzahl der pa rallel zur Flächennorma len dAn befindlichen magnetischen
Feldlinien entspricht (Bild 4-93 a). Die Anza hl der magneti schen Feldlinien wird in
Analogie zu Wasserfl üssen der magnetische
Fluß C/J gena nnt. Der Fluß durch die Leiterschleife ändert sich durch das Herausziehen
de r Leiter chleife von ursprünglich C/J auf null
--l I-dt
Bild 4-93.
Spannungsstoß und magnetischer Fluß.
um t-,.C/J = C/J - 0 = C/J. Die Änderung des magnetischen Flusses wird direkt dem Spannungsstoß zugeordnet:
t-,.C/J
=
JU(t) dt
(4-197)
N
l
Entsprechend gilt für den Spannungsstoß
J U(/) dt =
(4-198)
N t-,.C/J.
~er Spannungsstoß
J
U dt ist gleich der
Anderung des magnetischen Flusses C/J, der
die Fläche eines Leiters senkrecht durchsetzt.
Die Einheit des Flusses ist I Vs = 1 Wb (Weber).
Wegen der Abhängigkeit des Spannungstoßes von der Größe und der Orienti erung
der Leiterschleifenfläche zur Richtung des
magneti schen Flusses wird außer der magne-
4.4. Magnetisches Feld
ti chen Feld tärke H eine weitere vektoriel1e
magnetische Feldgröße, die magnetische Flußdichte oder die magnetische Induktion B
definiert:
f/J
B= A
bzw.
df/J
dA
(4-199)
Die magneti che Induktion oder Flußdichte B beschreibt den magnetischen
Fluß f/J pro Flächeneinheit. Die Richtung von B ist die Richtung des magnetischen FI usses.
Die Einheit der magnetischen Induktion ist
I Vs/m 2 = I T (Tesla).
Aus GI. (4-199) läßt sich der magnetische
Fluß f/J durch eine Fläche z. B. einer beliebig
orientierten Leiterschleife berechnen:
magnetische Feldstärke H, z. B. in einer langen Zylinderspule, und die magnetische Flußdichte B, z. B. bestimmt aus dem Spannungsstoß in einer nach Bild 4-94 im Winkel tp zur
Zylinderspulenachse herausgezogenen Leiterschleife, stets gleichgerichtet und zueinander
proportional. Es gilt die Beziehung
(4-201)
J
JB cos tp dA .
(4-200)
Sind also die magnetischen Feldlinien unter
einem Winkel tp zur Flächennormalen geneigt,
so ist nur die Flußdichte senkrecht zur Fläche
B cos tp maßgebend, wie Bild 4-94 zeigt.
Die magnetische Flußdichte B und die magnetische Feldstärke H dienen beide zur Beschreibung der Richtung und Stärke einer
magnetischen Wirkung. Im Vakuum sind die
I
Die Proportionalitätskonstante ist die magnetische Feldkonstante #0. Ihr Zahlenwert ergibt
sich aus den Kraftwirkungen elektrischer
Ströme (s. Definition des Ampere in Abschn.
1.3.1 und 4.1 .2).
Die magnetische Feldkonstante beträgt demnach
#0
cl> = B dA =
293
Vs
Am
Vs
Am
= 4 n' \ 10- 7 --;::::; 1,257' 10- 6 - - .
(4-202)
GI. (4-201) gilt nur im materieJreien Raum.
4.4.3.2. Kraftwirkungen im Magnetfeld
Verschiedene Magnetfelder überlagern sich
zu einem resultierenden Magnetfeld, z. B. das
Magnetfeld eines Permanentmagneten und
das eines stromdurchflossenen Leiters. Aus
diesem resultierenden Feld lassen sich Kraftwirkungen ableiten.
Stromdurchflossener Leiter im Magnetfeld
Bild 4-94. Beliebig
Magnetfeld.
orientierte
Leiterschleife im
Bild 4-95 a zeigt einen stromdurchflossenen
Leiter im Feld eines Permanentmagneten. Die
im mathematisch negativen Sinne umlaufenden magnetischen Feldlinien des stromdurchflossenen Leiters überlagern sich mit den vom
Nord- zum Südpol laufenden Feldlinien des
Permanentmagneten, wie Bild 4-95 b zeigt.
Das resultierende Feld hat in diesem Fal1 eine
Feldlinienverdichtung auf der linken und eine
Feldlinienverdünnung auf der rechten Seite.
Auf den Leiter wird eine Kraft in Richtung
der Feldverdünnung (nach rechts) wirksam.
Experimentel1 gilt für den Kraftbeitrag dF
eines stromdurchflossenen Leiterelementes der
Länge dl
294
4. Elektrizität und Magnetismus
a)
I (I)
F
s
b)
B
B
F
Magnetfeldlinien des
Leiters
I
N
Bild 4-95.
Kraftwirkung auf einen stromdurchflossenen Leiter im Magnetfeld.
dF=I(d/xB).
(4-203)
I
Verläuft der stromführende Leiterabschnitt
mit der Länge' senkrecht zum Magnetfeld, so
gilt
I
I
I
F= I J(d/x B) = - I JB x d/= - IB x Jd/ ,
o
0
0
F= - IB x l oder
F=I(lxB) .
(4-204)
Die Kraft auf einen strom durchflossenen Leiter hat den Betrag
(4_-2_0_5)~J
IL_F
_ =_I_' _B_SI_·n_rp_._ _ _ _ _ _
rp ist der Winkel zwischen Magnetfeld Bund
dem geraden Leiterstück I.
Die Kraft F auf einen stromdurchflossenen Leiter der Länge 1 in einem Magnetfeld B wirkt senkrecht zur Fläche, die von
den Vektoren I und B aufgespannt wird.
(Veranschaulichung durch die Rechte-HandRegel: Daumen in Stromrichtung, Zeigefinger
in magnetischer Feldrichtung: dann zeigt der
Mittelfinger in Kraftrichtung.)
4.4. Magnetisches Feld
Befindet sich der stromdurchflossene Leiter
senkrecht zum Magnetfeld, dann gilt (da
sin!p = I):
F= 1/B.
(4-206)
I
Gemäß GI. (4-206) läßt sich die magnetische
Induktion B über die Kraftwirkung im Magnetfeld erklären:
F
B=1/.
(4-207)
Die magnetische Flußdichte B gibt an,
wie groß die Kraft ist, die je Stromstärkeund je Längeneinheit auf einen stromdurchflossenen Leiter wirkt.
Die Einheit von B ist damit auch IN/Am.
Beispiel
4.4-3: Zwischen den kreisförmigen Polen eines Permanentmagneten befindet sich ein Weicheisenkern,
der 100 Wicklungen einer quadratischen Leiterschleife mit der Kantenlänge 1= 3 cm trägt (Prinzip
des Drehspulinstrumentes gemäß Bild 4-96). Die Induktion beträgt B = 2,5 T, und die Wicklungen werden von einer Stromstärke 1= 4,8 A durchflossen.
a) Welches Drehmoment erfährt ein Zeiger, und
wie groß ist der Winkelausschlag bei einer Winkelrichtgröße von c· = 3· 10- 2 Nm/ O ?
b) Wie groß ist die Stromstärke bei einem Zeigerausschlag von 40 ° ?
295
Ferner gilt
M
M= c· rp oder rp=-= 36 o.
c·
b) Es gilt für das Drehmoment M= c· rp=N I B12.
Daraus folgt für die Stromstärke
c· rp
1= NBI2 = 5,33 A.
Magnetisches Moment
Eine weitere wichtige magnetische Kenngröße
ist das magnetische Moment m. Es wird analog
zum elektrischen Dipolmoment (GI. (4-168»
definiert:
m=<I>I.
(4-208)
I ist der fiktive Abstand zwischen Nord- und
Südpol.
Dabei steht anstelle der Ladung Q die magnetische Polstärke <1>. Sie errechnet sich aus der
Kraft je magnetischer Feldstärke <I> = FI H
(analog zur elektrischen Ladung Q als Quotient aus Kraft und elektrischer Feldstärke
Q = F/E).
Das magnetische Moment m wird durch die
Messung eines Drehmomentes M in einem
äußeren Magnetfeld bestimmt. Je nachdem,
ob das äußere Magnetfeld durch die magnetische Flußdichte B bzw. durch die magnetische Feldstärke H beschrieben wird, ergibt
sich das Amperesche magnetische Moment
mA , das vor allem in der Atomphysik verwendet wird, bzw. das Coulombsche magnetische
Moment me:
<I> . I
mA=-/10
IMI
ImA I =!BT'
M=mAxB
(4-210)
M= me xH
(4-211)
me = <I> I
Bild 4-96.
Prinzip des Drehspulinstrumentes.
Lösung:
Für die magnetische Kraft Fmagn gilt nach GI.
(4-206) F magn = NIl B .
a) Es ergibt sich ein Drehmoment von
M=Fmagn/= NIBI2
=
1,08 Nm.
I
I me l
IMI
=THT
'
Das magneti che Moment m ist der Quotient aus dem Drehmoment der magnetischen Kraft und dem magnetischen Feld
(B oder H) . Der Vektor des magnetischen
Momentes zeigt vom Süd- zum Nordpol.
Bild 4-97 verdeutlicht den Zusammenhang.
296
4. Elektrizität und Magnetismus
e
ew
Es ist I = - = - , so daß man schrei ben kann
To 2 n
F
--------------~~~-----------------B
2
ew
2n
ewr 2
__________~~~L------------------(H) mA = nr - = - - - - .
F
Für ein Elektron mit Drehimpuls f1 wird das magnetische Moment
..
Bild 4-97.
2
e '1
mA=--=9,27
· 1O - 24 Am 2 .
2m e
Magnetisches Moment.
Eine vom Strom / durchflossene Schleife der
Fläche A erfährt in einem äußeren Magnetfeld mit der Induktion B ein Drehmoment M,
das versucht, die Schleifenfläche senkrecht zu
den Feldlinien zu stellen. Es gilt M = mA x B
mit
(4-211)
I
Der Vektor des magnetischen Moments mA
steht senkrecht auf der Schleifenfläche.
Dieser Wert wird als Bohrsches Magneton IJB bezeichnet (Abschn. 8.3).
Kraft zwischen zwei parallelen
stromdurchflossenen Leitern
Befinden sich zwei stromdurchflossene Leiter
im Abstand d voneinander, so spürt der Leiter
I das Magnetfeld des Leiters 2. Dessen magnetische Feldstärke ist gemäß GI. (4-183)
/2
Beispiel
H 2 = 2nd·
4.4-4: Das magnetische Moment mA eines Elektrons, das mit der Winkelgeschwindigkeit w im Abstand r um den Atomkern kreist, ist zu berechnen.
Für die Kraft zwischen zwei Leitern gilt entsprechend GI. (4.206)
FI2 = /1 1/10 H 2
Lösung:
Es gilt nach GI. (4-211) mA = A I.
a)
und unter Berücksichtigung von H 2
b)
J t
Schwächung
des Feldes
I
~
"t
!,
2
Verstärkung
des Feldes
Bild 4-98. Kraft zwischen zwei
parallelen stromdurchj1ossenen
Leitern.
4.4. Magnetisches Feld
(4-212) I
Bild 4-98 zeigt die Überlagerung der magnetischen Feldlinien für zwei parallele stromdurchflossene Leiter. Bei zwei gleichgerichteten Strömen wirkt zwischen den Leitern eine
Anziehungskraft (Bild 4-98 a), während bei
entgegengesetzt fließenden Strömen zwischen
den Leitern eine Abstoßungskraft wirkt (Bild
4-98 b).
Kraft auf bewegte Ladungsträger im
Magnetfeld
Bewegte Ladungsträger erfahren im Magnetfeld eine Kraft. GI. (4-203)
dF= I(d!x B)
läßt sich für diesen Fall umformen: Für die Geschwindigkeit der Ladungsträger gilt v = dl/dt,
hieraus folgt d! = v dt. Eingesetzt ergibt dies
dF= I dt(vx B).
Mit I dl
=
dQ erhält man dF= dQ(v x B) oder
(4-213)
Bewegt sich eine Ladung Q mit der Geschwindigkeit v durch ein Magnetfeld der
magnetischen Induktion B, so spürt die
Ladung eine Kraft. Diese wirkt senkrecht
zu v und senkrecht zu B.
Bild 4-99 verdeutlicht den Zusammenhang.
Die Kraft wird nach ihrem Entdecker LorentzKraji genannt (H. A. LORENTZ, 1853 bis
1928). Der Betrag der Lorentz-Kraft ist
297
Die Lorentz-Kraft ist demnach maximal, wenn
v und B senkrecht zueinander stehen und null,
wenn sich die Ladungsträger in Richtung des
magnetischen Feldes bewegen.
Sind die fließenden Ladungen in einem Leiter Elektronen, so erfahren die mit einer Geschwindigkeit Vel in x-Richtung fließenden
Elektronen in einem Querfeld B y in y-Richtung eine Lorentz-Kraft in z-Richtung. Sie
beträgt je Elektron
(4-215)
Sie wirkt wegen der negativen Ladung der
Elektronen in die negative z-Richtung.
Hall-Effekt
Durch ein leitendes Plättchen mit der Breite b
und der Dicke d fließe in x-Richtung ein
Strom Ix. Senkrecht hierzu herrsche ein
Magnetfeld B z . Dann wirkt aufjedes Elektron die
Lorentz-Kraft
F Ly = - e V x B z .
Durch diese Lorentz-Kraft werden die Elektronen in y-Richtung verschoben, so daß an der
linken Stirnseite ein Elektronenüberschuß und
an der rechten Stirnseite ein Elektronenmangel herrscht, wie Bild 4-100 zeigt Dies hat
zur Folge, daß in y-Richtung ein elektrisches
Gegenfeld aufgebaut wird und eine elektrische Gegenkraft F el = - e Ey auftritt. Die Verschiebung der Elektronen aufgrund der Lorentz-Kraft kommt dann zum Stillstand, wenn
sich ein Gleichgewicht der Kräfte einstellt:
Fel =FLy oder -eEy =-e vx B z •
Es ist E y = Uyf b, so daß für die zwischen
[
IFL I=QvBsin(v,B).
(4-214)
I
den Stirnseiten in y-Richtung meßbare Spannung Uy folgt
y
V"
' ~~~~----------V"
I
Bild 4-99. Kraft auf bewegte
(negative) Ladungsträger im
Magnetfeld
298
4. Elektrizität und Magnetismus
den zur Me ung on Magn tfeldern verwendet. In Hall-Generator n g hieht di Multiplikation zweier eleklri her r"ß n (Ix Bz)
durch M ung der Hall pannuog UH •
Bei dem von K. . KLITZf G eold ckten Quanten-Hall-Effekt i t der Ha/l-Wide~ land RH
gequantelt. Er hat eine große Bed utung al
Widerstand normal ( b chn. 4 . 1.4 und .2.5).
Mit Hilfe des Hall-Koeffizienten A H können
folgende phy ikali che Größen ermittelt werden :
Bild 4-100.
- die Ladung trägerkonzentration n (wichtig
u. a. bei Halbleitern s. Ab chn. 9.2.3),
- das Vorzeichen der Ladung träger (Löcherleitung plus und Elektronenleilung minus),
- die Ladungsträgerbeweglichkeit Jl = xA H •
Hall-Effekt (negative Ladungsträger).
(4-216)
Die Spannung UH wird Hall-Spannung genannt(E. H. HALL, 1855 bis 1938).
Die Stromdichte jx der Elektronen in x-Richtung ist
(4-217)
I
Dabei ist n die Anzahl der Elektronen je
Volumen und e die Elementarladung. Eingesetzt in die Gleichung für die Hall-Spannung
ergibt sich
Tabelle 4-9 zeigt die Werte des Hall-Koeffizienten AH für einige ausgewählte Werkstoffe.
Tabelle 4-9. Hall-Koeffizienten einiger Werkstoffe.
m3
A H in 10- 11 - C
Werkstoff
ElektronenJeitung
Kupfer
Gold
Natrium
Caesium
Cu
Au
Na
Cs
Der Faktor
wird Hall-Koeffizient AH
ne
genannt:
I
AH = - ·
ne
(4-219)
Löcherleitung
Cadmium Cd
Zinn
Sn
Beryllium Be
+ 6
+ 14
+24,4
Halbleiter
Somit kann GI. (4-218) geschrieben werden
(4-220)
- 5,5
-7,5
- 25
- 28
Wismut
IodiumArsenid
Bi
- 5 · 10 4
IoAs
- 10 7
Wegenjx = Ix/(b d) gilt
(4-221)
Da die Hall-Spannung proportional zur magnetischen Ind uktion B ist, werden H all-Son-
Beispiel
4.4-5: Durch eine 0,1 mm dicke Silberfolie fließt
ein Strom von 4 A Im senkrecht zur Folie befindlichen Magnetfeld (B = 6,2 Vs/m 2 ) wird eine HallSpannung UH = - 22 ~V gemessen. Bestimmt wer-
4.4. Magnetisches Feld
den sollen die Hall-Konstante AH von Silber, die Ladungsträgerkonzentation n und die Elektronenbeweglichkeit jl.
mv
r=--
299
(4-222) ;
QB '
Lösung :
Nach GI. (4-221) gilt für den Hall-Koeffizienten
AH=
3
UHd
1B
-- = -
m
C .
8 87 . 10- 11 '
1
Aus GI. (4-219) ergibt sich n =_1_ = 7 · 1028 _ _.
AHe
m3
Aus AH =.!!..- resultiert
x
11 = A H X ( XSilber = 6,25 ' 10 7 -1-) = 5,54 ' 10- 3 -m
Qm
2
Vs
.
Kraftwirkungen auf frei bewegliche
Ladungsträger
Bewegen sich freie Ladungsträger (z. B. Elektronen in einem Oszilloskop oder Protonen
in einem Beschleuniger) mit einer konstanten
Geschwindigkeit v in einem magnetischen
Querfeld, so wirkt auf sie die Lorentz-Kraft
F L = Q (v x B) . Sie steht - analog zur Zentripetalkraft einer Kreisbewegung in der Mechanik - senkrecht zur Geschwindigkeit v
und ändert lediglich die Richtung, nicht aber
d~n Betrag der Teilchengeschwindigkeit, wie
BIld 4-101 a zeigt. Deshalb führen die geladenen Teilchen im Magnetfeld eine Kreisbewegung aus, wenn sie mit konstanter Geschwindigkeit v in ein homogenes magnetisches
Querfeld gelangen (Bild 4-10 I b). Durchlaufen geladene Teilchen einen Kreis mit dem
Radius r, so ist die Zentrifugalkraft gleich der
Lorentz- Kraft:
m v2
--= Q v B
r
a)
Diese Beziehung zeigt, daß bei konstantem
magnetischen Querfeld der Bahnradius um so
kleiner wird, je größer das Magnetfeld ist. Mit
zunehmender Geschwindigkeit der geladenen
Teilchen wird der Radius größer. Dies wird
bei den Teilchenbeschleunigern ausgenutzt. In
Bild 4-102 erkennt man das Prinzip. Bei
einem Z yklotron herrscht ein konstantes Magnetfeld, und die Teilchen werden durch ein
elektrisches Wechselfeld zwischen den Bereichen I und Il auf höhere Geschwindigkeiten
gebracht (Bild 4-102a). Dadurch entsteht eine
spiralförmige Bahn, die aus aneinandergrenzenden Halbkreisen besteht. (Bei hohen Teilchengeschwindigkeiten ist der relativistische
Massenzuwachs zu berücksichtigen, s. Abschn.
10.4.)
In einem Synchrotron (Bild 4-102 b) bleibt der
Radius der beschleunigten Teilchen gleich,
weil entsprechend der zunehmenden Geschwindigkeit v das Magnetfeld B ebenfalls erhöht
wird.
Aus GI. (4-222) ist auch die spezifisch e L adung eines Elementarteilchens bestimmbar:
g=-~'
m
(4-223)
rB
F ür ein Elektron gilt dann
Q -e
C
- = - = - 1 ,76 ' 10"- .
m me'
kg
oder
(4-224)
b)
v
(0
(0
(0
(0
(0
(0
(0
(0
(0
FL
~
(0
(0
(0
(0
(0
(0
(0
(0
(0
(0
(0
(0
Bild 4-101. Kreisbewegung f reier
Elektronen im Magnetfeld.