Übungen zur Physik I fuer Chemiker und Lehramt mit

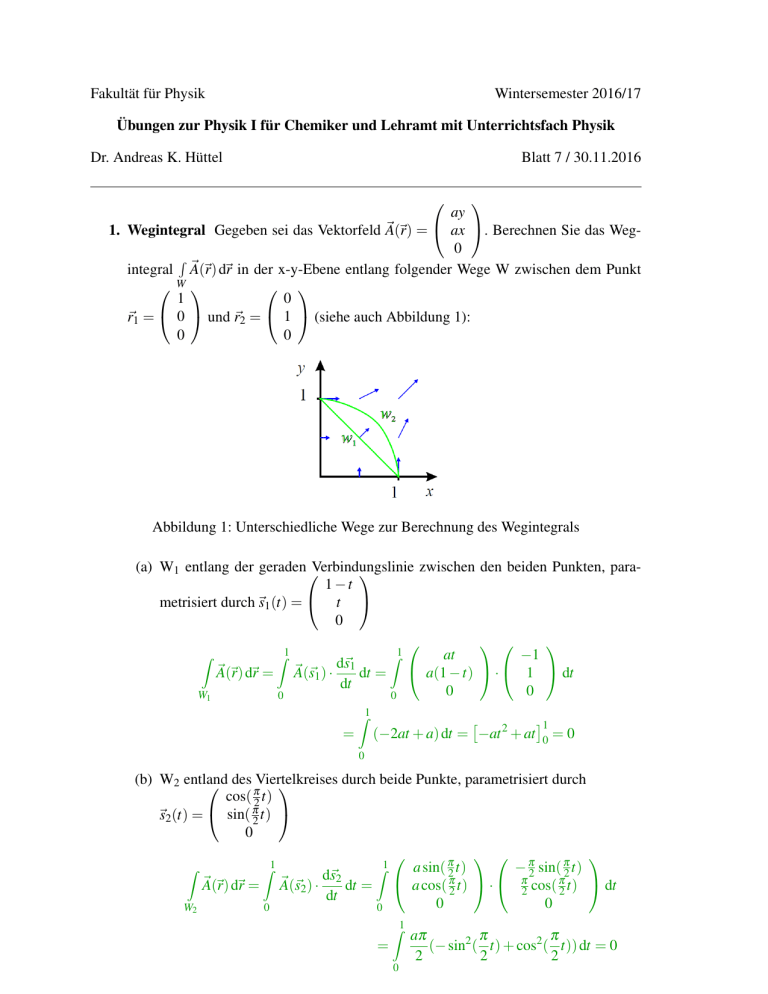
Fakultät für Physik
Wintersemester 2016/17
Übungen zur Physik I für Chemiker und Lehramt mit Unterrichtsfach Physik
Dr. Andreas K. Hüttel
Blatt 7 / 30.11.2016


ay
1. Wegintegral Gegeben sei das Vektorfeld ~A(~r) =  ax . Berechnen Sie das Weg0
R
~
integral A(~r) d~r in der x-y-Ebene entlang folgender Wege W zwischen dem Punkt
W
 
1
0



0
1  (siehe auch Abbildung 1):
~r1 =
und ~r2 =
0
0
Abbildung 1: Unterschiedliche Wege zur Berechnung des Wegintegrals
(a) W1 entlang der geradenVerbindungslinie
zwischen den beiden Punkten, para
1−t

t 
metrisiert durch ~s1 (t) =
0
Z
~A(~r) d~r =
W1
Z1
~A(~s1 ) · d~s1 dt =
dt
0
Z1
0
Z1
=

 

at
−1
 a(1 − t)  ·  1  dt
0
0
1
(−2at + a) dt = −at 2 + at 0 = 0
0
(b) W2 entland
durch beide Punkte, parametrisiert durch
 des πViertelkreises

cos( 2 t)
~s2 (t) =  sin( π2 t) 
0
Z
W2
~A(~r) d~r =
Z1
0
~A(~s2 ) · d~s2 dt =
dt
Z1
0

  π

a sin( π2 t)
− 2 sin( π2 t)
 a cos( π t)  ·  π cos( π t)  dt
2
2
2
0
0
Z1
=
0
aπ
π
π
(− sin2 ( t) + cos2 ( t)) dt = 0
2
2
2
Daß das letzte Integral Null ergibt kann man mit Hilfe der Regel zur
partiellen Integration relativ leicht herleiten, über
Z
(sin x)0 (cos x) d x = (sin x)(cos x) −
Z
(sin x)(cos x)0 d x
Alternativ schlägt man eine Formel dafür im Bronstein nach.
2. Vollkommen elastischer Stoß Zwei Teilchen mit den Massen m1 = m und m2 = 3m
stoßen vollkommen elastisch zentral zusammen. Vor dem Stoß sollen beide Teilchen
eine entgegengesetzt gleiche Geschwindigkeit haben, also
v1i = −v2i = v.
(a) Stellen Sie den Energieerhaltungssatz auf und setzen Sie die Angaben ein.
1
1
1
1
m1 v21i + m2 v22i = m1 v21 f + m2 v22 f
2
2
2
2
2
2
2
⇒ 4v = v1 f + 3v2 f
(1)
(2)
(b) Stellen Sie den Impulserhaltungssatz auf und setzen Sie die Angaben ein.
m1 v1i + m2 v2i = m1 v1 f + m2 v2 f
⇒ −2v = v1 f + 3v2 f
(3)
(4)
(c) Wie groß sind die Geschwindigkeiten v1 f und v2 f nach dem vollkommen elastischen Stoß? Leiten Sie diese mit Hilfe von (a) und (b) her!
Aus 4 folgt
v1 f = −2v − 3v2 f
(5)
Einsetzen in 2 und Ausmultiplizieren ergibt
⇒
v2 f
0 = v2 f (12v + 12v2 f )
=0
oder
v2 f = −v
(6)
(7)
Da vor dem Stoß v2i = −v gilt, muss die Geschwindigkeit nach dem
Stoß v2 f = 0 sein. Damit erhält man
v1 f = −2v .
(8)
3. Billiardkugel Eine Billardkugel mit einer Geschwindigkeit ~u1 trifft reibungsfrei auf
eine zweite, ruhende Billardkugel, welche um den halben Kugeldurchmesser versetzt
zur Bewegungsrichtung still steht (vgl. Abbildung 2). Wir nehmen an, daß ein perfekt
elastischer Stoß stattfindet.
(a) Stoßen sich die Kugeln im rechten Winkel ab? Wenn ja, warum?
Abbildung 2: Nicht zentraler Stoß zweier Kugeln mit gleicher Masse
Impulserhaltung: m · u~1 = m · v~1 + m · v~2
u~1 = v~1 + v~2
u~1 2 = v~1 2 + v~2 2 + 2~
v1 · v~2
Ekin,vorher = Ekin,nachher + m · v~1 · v~2
Die Verformungsenergie verschwindet genau dann wenn, v~1 und v~2 senkrecht zueinander stehen oder mindestens einer der beiden Vektoren gleich
0 ist.
(b) Bestimmen Sie Richtung und Geschwindigkeit beider Kugeln nach dem Stoß
Hinweis: Fertigen Sie eine Skizze an, mit allen relevanten Vektoren und Winkeln
Abbildung 3: Lösungsskizze zur Aufgabe 3b)
Aus der räumlichen Anordnung der Kugeln bei Berührung, siehe Skizze, ist klar, daß α2 = 30◦ gelten muß. Mit a) folgt α1 = 60◦ .
Impulserhaltung in x-Richtung: u1 = v1,x + v2,x
Impulserhaltung in y-Richtung: v1,y = −v2,y
Insgesamt folgt (siehe Skizze)
1
v1 = u1 · cosα1 = u1
√ 2
3
v2 = u1 · cosα2 =
· u1
2
4. Inelastischer Stoß: Kleinstwagen gegen Geländewagen Wir schauen uns zwei Fahrzeugtypen an, einen Kleinstwagen und einen Geländewagen.
(a) Berechne die kinetische Energie, die die zwei Fahrzeuge mit den Massen m1 =
900 kg und m2 = 2, 7 t bei einer Geschwindigkeit von 50 km/h besitzen.
Kleinstwagen: Ekin = 86, 8 kJ
Geländewagen: Ekin = 260, 4 kJ
(b) Auf welche Höhe könnten sie mit dieser Energie im als konstant angenommenen
Schwerefeld der Erde (g = 9,81 m/s2 ) angehoben werden?
mgh = Epot = Ekin
Daraus folgt
hmax =
v2
2g
Die Massen kürzen sich heraus, für beide Fahrzeuge ergibt sich hmax =
9, 83 m. Umgekehrt bedeutet dies, dass beim Sturz aus etwa 10 m Höhe
eine Geschwindigkeit von 50 km/h erreicht werden kann.
Die zwei Autos prallen nun frontal zentral aufeinander in einem inelastischen Stoß.
Dabei verkeilen sie sich so, daß sie nach dem Stoß mit gemeinsamer Geschwindigkeit
v0 weiterrollen. Vor dem Stoß gilt: v1 =−v2 = 50 km/h. m1 = 900 kg, m2 =2,7 t.
(c) Stellen Sie die Gleichungen für Energie- und Impulserhaltung auf!
(I) Impulserhaltungssatz:
(m1 + m2 )v0 = m1 v1 + m2 v2 = (m1 − m2 )v1
(II) Energieerhaltungssatz:
1
1
1
(m1 + m2 )v02 = m1 v21 + m2 v22 + Q
2
2
2
(d) Berechnen Sie die Geschwindigkeit v0 nach dem Stoß!
Umformung von Gleichung (I):
m1 − m2
v1 = v0
m1 + m2
v0 = −25 km/h = −6.9 m/s
D.h. der Geländewagen und der Kleinstwagen bewegen sich mit halbierter Geschwindigkeit in die ursprüngliche Bewegungsrichtung des
Geländewagens!
(e) Wieviel kinetische Energie geht “verloren”, wird also in Verformungsenergie
oder Wärme umgewandelt?
Kinetische Energie nach dem Stoß:
1
0
Ekin
= (m1 + m2 )v02 = 86, 8 kJ
2
Kinetische Energie vor dem Stoß (aus Aufgabe 3a):
Ekin = 260, 4 kJ + 86, 8 kJ = 347, 2 kJ
Umgewandelte Energiemenge:
Q = 260, 4 kJ
(f) Berechnen Sie die Impulsänderungen ∆p1 und ∆p2 der beiden Autos.
∆p1 = m1 v0 − m1 v1 = m1 (v0 − v1 ) = −18750kg · m · s−1
∆p2 = m2 v0 − m2 v2 = m2 (v0 − v2 ) = 18750kg · m · s−1
Die Impulsänderungen addieren sich zu Null, denn die Fahrzeuge tauschen nur einen Teil ihrer Impulse aus (abgeschlossenes System ohne
äußere Kräfte).