Übungen zur Physik I fuer Chemiker und Lehramt mit

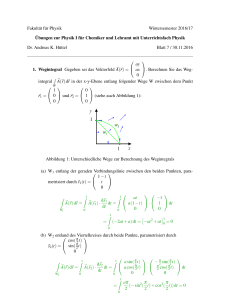
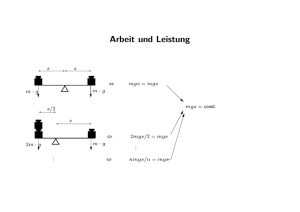
Fakultät für Physik
Wintersemester 2015/16
Übungen zur Physik I für Chemiker und Lehramt mit Unterrichtsfach Physik
Dr. Andreas K. Hüttel
Blatt 7 / 1.12.2015
1. Quantenmechanik Ein Teilchen der Masse m bewege sich mit der Geschwindigkeit
v in einem Potential Epot (x) = V (x).
(a) Stellen Sie die kinetische Energie T als Funktion des Impulses p des Teilchens
auf.
(b) Stellen Sie den Energieerhaltungssatz auf.
(c) Die zeitunabhängige Schrödingergleichung in einer Dimension, mit die grundlegendste Gleichung der Quantenmechanik, lautet
)
(
d 2
1
−ih̄
+V (x) ψ(x) = Eψ(x) .
(1)
2m
dx
Dabei ist ψ(x) eine Funktion von x mit komplexem Wert (die “Wellenfunktion”), i die imaginäre Einheit mit i2 = −1, und h̄ = 1.054571800 · 10−34 Js die
sogenannte reduzierte Planck-Konstante. Der Impulsoperator p̂ ist definiert als
p̂ = −ih̄
d
.
dx
(2)
Setzen Sie den Impulsoperator in die Schrödingergleichung ein und vergleichen
Sie ihr Ergebnis mit (b). Was fällt Ihnen auf?
2. Vollkommen elastischer Stoß Zwei Teilchen mit den Massen m1 = m und m2 = 3m
stoßen vollkommen elastisch zentral zusammen. Vor dem Stoß sollen beide Teilchen
eine entgegengesetzt gleiche Geschwindigkeit haben, also
v1i = −v2i = v.
(a) Stellen Sie den Energieerhaltungssatz auf und setzen Sie die Angaben ein.
(b) Stellen Sie den Impulserhaltungssatz auf und setzen Sie die Angaben ein.
(c) Wie groß sind die Geschwindigkeiten v1 f und v2 f nach dem vollkommen elastischen Stoß? Leiten Sie diese mit Hilfe von (a) und (b) her!
3. Inelastischer Stoß: Auto gegen Betonpfeiler – die Knautschzone Wir betrachten
den inelastischen Stoß eines Autos gegen einen Betonpfeiler. Das Auto soll dabei soweit verformt werden, dass die gesamte kinetische Energie in Wärme / Verformungsarbeit umgewandelt wird. Wir schauen uns zwei Fahrzeugtypen an, einen Kleinstwagen
und einen Geländewagen.
(a) Berechne die kinetische Energie, die die zwei Fahrzeuge mit den Massen m1 =
900 kg und m2 = 2, 7 t bei einer Geschwindigkeit von 50 km/h besitzen. Auf welche Höhe könnten sie mit dieser Energie im als konstant angenommenen Schwerefeld der Erde (g = 9,81 m/s2 ) angehoben werden?
(b) Beide Autos verfügen über Knautschzonen unterschiedlicher Länge, d.h. über
Bereiche, die gezielt kinetische Energie in Verformungsarbeit umwandeln können. Für den Kleinstwagen sei die Länge der Knautschzone 40 cm, für den Geländewagen 1,20 m. Nimm an, dass die Fahrzeuge von ihrer Ausgangsgeschwindigkeit aus innerhalb der Länge der Knautschzone mit konstanter Beschleunigung
auf Geschwindigkeit Null abgebremst werden, und gib die Werte für diese Beschleunigung (in m/s2 und in Vielfachen von g) während des Aufpralls bei beiden
Fahrzeugen an.
(c) Nach dem Stoß sehen wir keine Bewegung der Fahrzeuge oder des Betonpfeilers
– ist die Impulserhaltung hier verletzt?
4. Inelastischer Stoß: Kleinstwagen gegen Geländewagen (Nur LA) Die zwei Autos aus der letzten Aufgabe prallen nun frontal zentral aufeinander in einem inelastischen Stoß. Dabei verkeilen sie sich so, dass sie nach dem Stoß mit gemeinsamer
Geschwindigkeit v0 weiterrollen. Vor dem Stoß gilt: v1 =−v2 = 50 km/h. m1 = 900 kg,
m2 =2,7 Tonnen.
(a) Stellen Sie die Gleichungen für Energie- und Impulserhaltung auf!
(b) Berechnen Sie die Geschwindigkeit v0 nach dem Stoß!
(c) Wieviel kinetische Energie geht “verloren”, wird also in Verformungsenergie
oder Wärme umgewandelt?
(d) Berechnen Sie die Impulsänderungen ∆p1 und ∆p2 der beiden Autos.
(e) Die Kilokalorie ist eine alte Nicht-SI-Einheit für die Energie. Nur so zum Spaß
und zum Vergleich der Größenordnungen: Dem Brennwert von wieviel Milliliter
Coca-Cola entspricht obige “verlorene” Energie? (Google hilft.)