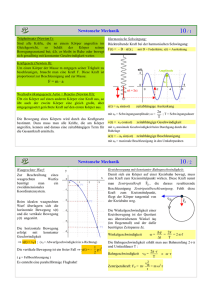
Zentraler, vollkommen inelastischer Stoß

Zentraler, vollkommen inelastischer Stoß
Kennzeichen:
Die kinetische Energie der zusammenstoßenden Körper wird teilweise in innere Energie umgewandelt.
Beim inelastischen Stoß gilt somit der Erhaltungssatz für die mechanische Energie nicht.
Man spricht vom vollkommen inelastischen Stoß, wenn die Partner ineinander verhaken und nach der
Wechselwirkung mit gleicher Geschwindigkeit weiterfliegen.
Für die Wechselwirkung gilt - wie immer - das Gesetz von Newton III ("actio gegengleich reactio")
und der daraus ableitbare Impulserhaltungssatz.
Bezeichnungen:
m1: Masse des Körpers 1
m2: Masse des Körpers 2
v1: Geschwindigkeit des Körpers 1 vor der
Wechselwirkung
v2: Geschwindigkeit des Körpers 2 vor der
Wechselwirkung
u: Geschwindigkeit der beiden "verhakten" Körper
nach der Wechselwirkung
vorher
Energie
nachher
ΔU: Änderung der inneren Energie
Impuls
Berechnung der Endgeschwindigkeit aus dem
Impulserhaltungssatz:
(es genügt eine Gleichung zur Berechnung der
einzigen Unbekannten u)
Berechnung der Energie ΔU, d.h. derjenigen
mechanischen Energie, die beim inelastischen Stoß
in innere Energie/Wärme umgesetzt wird:
Aufgabe 1:
1a) Leiten Sie die Formel für ΔU her.
1b) Geben sie die Formel für ΔU bezogen auf folgende Sonderfälle an:
b1)
Gleiche Massen; Körper 2 ruht
Geg.: m1 = m2= m; v2 = 0;
b2)
Gleiche Massen; Körper 1 und Körper 2 haben entgegengesetzt gleiche Geschwindigkeiten
Geg.: m1 = m2= m; v1 = - v2;
b3)
Die Masse des ruhenden Körpers 2 ist wesentlich größer als die Masse von Körper 1.
Geg.: m1 << m2= m; v2 = 0;
Zentraler, vollkommen elastischer Stoß
Kennzeichen:
Die kinetische Energie der zusammenstoßenden Körper wird nicht in innere Energie umgewandelt.
Beim elastischen Stoß gilt somit der Erhaltungssatz für die mechanische Energie und der
Impulserhaltungssatz. Man spricht vom vollkommen elastischen Stoß.
Für die Wechselwirkung gilt - wie immer - das Gesetz von Newton III ("actio gegengleich reactio")
und der daraus ableitbare Impulserhaltungssatz.
Aufgabe2
Berechne über Energie- und Impulserhaltung die Geschwindigkeiten der Kugeln in x-Richtung nach
dem Stoß
Aufgabe 3
Ballistisches Pendel
Das Bild zeigt ein Projektil bekannter Masse mP in g das in einen
Holzklotz der Masse MK = 5,0 kg eindringt und dort stecken bleibt.
Der an Fäden aufgehängte Klotz schwingt ballistisch und seine
Höhenzunahme h kann in cm abgelesen werden (Bild unten nach dem
Stoß).
a) Zeigen Sie, dass sich unter der Verwendung des Energie- und
Impulserhaltungssatzes für die Projektil-geschwindigkeit des
Geschosses vor dem Stoß die Formel vP = 1/MK (mP+MK) (2gΔh)1/2
ergibt
b) Bestimmen Sie aus den Angaben des unteren Bildes die
Geschwindigkeit vP des Projektils.
Lösungen:
1a)
:
1 b1 Gleiche Massen; Körper 2 ruht
Geg.: m1 = m2= m; v2 = 0;
Ergebnis:
Die beiden Körper bewegen sich nach der Wechselwirkung mit "halber Geschwindigkeit"
weiter;
Beim Stoß wird die Hälfte der ursprünglich vorhandenen kinetischen Energie in innere
Energie umgesetzt.
1 b2 Gleiche Massen; Körper 1 und Körper 2 haben entgegengesetzt gleiche
Geschwindigkeiten
Geg.: m1 = m2= m; v1 = - v2;
Ergebnis:
Die beiden Körper ruhen nach der Wechselwirkung.
Beim Stoß wird die gesamte, ursprünglich vorhandene kinetische Energie in innere Energie
umgesetzt.
1 b3 Die Masse des ruhenden Körpers 2 ist wesentlich größer als die Masse von Körper 1.
Geg.: m1 << m2= m; v2 = 0;
Ergebnis:
Die beiden Körper ruhen nach der Wechselwirkung.
Beim Stoß wird die gesamte, ursprünglich vorhandene kinetische Energie in innere Energie
umgesetzt.
Aufgabe 2
Aufgabe 3
3a)
Herleitung:
Es findet zunächst ein vollkommen unelastischer Stoß statt, bei dem der Impuls des
Projektils vollständig in den Impuls von Klotz und darin steckendem Projektil
übergeht:
m·vP = (M + m)·vK
=>
Anschließend wird die kinetische Energie des Klotzes in potentielle Energie des
Klotzes umgewandelt.
=>
=>
Beispiel: m = 10g = 0,010 kg; M = 5,0kg;  h = 10cm = 0,10m
Vorsicht, die im Applet angegeben Lösungen täuschen eine zu große Genauigkeit
vor, die Genauigkeit ist sinnvollerweise nur 2 gültige Ziffern.