Ubungsblatt 11 - Institut für Formale Methoden der Informatik
Werbung

Datenstrukturen und Algorithmen
Funke/Weiß
Institut für Formale
Methoden der Informatik
Universität Stuttgart
SS 2012
http://www.fmi.informatik.uni-stuttgart.de/alg
Übungsblatt 11
Abgabe: 4. Juli 2012; 23:59 Uhr
Problem 1 (5 P.)
Eine weitere Möglichkeit (neben Verkettung), um Kollisionen beim Hashing aufzulösen, ist die sogenannte lineare
Sondierung. Dazu wird eine Konstante c fest gewählt. Falls ein Element an einer Position, die schon belegt ist, in
die Hashtabelle eingefügt weden soll, wird solange die Konstante c auf die Position addiert, bis eine freie Stelle
gefunden wird (modulo der Länge der Hashtabelle). Ein Element x wird somit an der freien Stelle h(x) + ic mod m
mit kleinstmöglichem i eingefügt (h ist hier die Hashfunktion, m die Länge der Hashtabelle).
a) Beschreiben Sie Prozeduren in Pseudocode für das Finden, Einfügen und Löschen von Elementen in Hashtabellen mit linearer Sondierung (Achtung: Beim Löschen ist Vorsicht geboten).
b) Warum sollte man c teilerfremd zur Länge der Hashtabelle wählen?
c) Was sind Vor- und Nachteile dieser Methode?
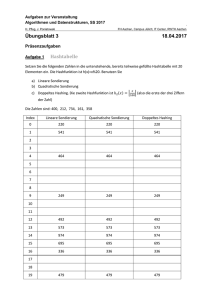
d) Fügen Sie die folgenden Zahlen in eine Hashtabelle der Länge 11 ein.
107, 50, 100, 102, 16, 25, 42, 36
Die Auflösung von Konflikten soll mit linearem Sondieren (mit c = 1) funktionieren. Als Hashfunktion soll
h(x) = x mod 11 verwendet werden. Geben Sie die fertige Hashtabelle im eClaus ab.
Problem 2 (5 P.)
a) Sei N eine Primzahl und seien 0 ≤ u, v, x, y < N natürliche Zahlen.
Zeigen Sie: Ist x 6= y, dann ist
(a, b) ∈ {0, . . . , N − 1} × {0, . . . , N − 1} ax + b ≡ u mod N, ay + b ≡ v mod N = 1.
b) Sei nun m ∈ N, U ⊆ {0, . . . , N − 1} und sei X = {ha,b | a, b ∈ {0, . . . , N − 1}} mit
ha,b : U → {0, . . . , m − 1},
x 7→ (ax + b mod N ) mod m.
Zeigen Sie:
X ist c-universell mit c =
2
N
m
·
.
m
N
Erinnerung: Eine Klasse von Hashfunktionen X heißt c-universell, falls für alle x 6= y ∈ U gilt:
|{h ∈ X | h(x) = h(y)}|
c
≤
|X|
m
Problem 3 (4 P.)
Fertigen Sie eine Zusammenfassung über die in der Vorlesung behandelten Sortierverfahren an. Listen Sie dabei
alle Verfahren auf und beschreiben kurz deren Funktionsweise. Geben Sie auch mittlere und worst-case Laufzeiten
(soweit bekannt) sowie die Vor- und Nachteile der jeweiligen Verfahren an.
Problem 4 (3 P.)
Um das k-kleinste Element einer Folge zu bestimmen, kann man das Feld sortieren und dann das Element mit
Index k ausgeben. Allerdings ist es nicht notwendig die komplette Folge zu sortieren, um das k-kleinste Element
zu bestimmen.
Modifizieren Sie den Quicksort-Algorithmus so, dass er zu einem Feld A[1..n] und einer Zahl k, 1 ≤ k ≤ n
das k-kleinste Element bestimmt ohne das Feld vollständig zu sortieren. Das Feld A kann danach in beliebiger
Reihenfolge vorliegen.
Schreiben Sie Ihr Programm in Pseudocode und begründen Sie kurz die Korrektheit.
Wie ist die worst-case Laufzeit Ihres Progammes? Was können Sie über die mittlere Laufzeit aussagen?
Problem 5 (3 P.)
Berechnen Sie eine topologische Sortierung des folgenden Graphen:
B
A
E
C
H
G
D
F
J
I
Besitzt der Graph mehrere topologische Sortierungen? Wenn ja, wie viele?
Welche Eigenschaften muss ein Graph besitzen, damit genau eine (eindeutige) topologische Sortierungen existiert?