Lösung 3

MAE1 – Mathematik: Analysis für Ingenieure 1
Dr. Christoph Kirsch
Herbstsemester 2013
ZHAW Winterthur
Lösung 3
Aufgabe 1 :
a) Die Betragsfunktion ist definiert für alle reellen Zahlen, also ist D = R der
grösstmögliche Definitionsbereich. Das Bild ist f (R) = [0, ∞).
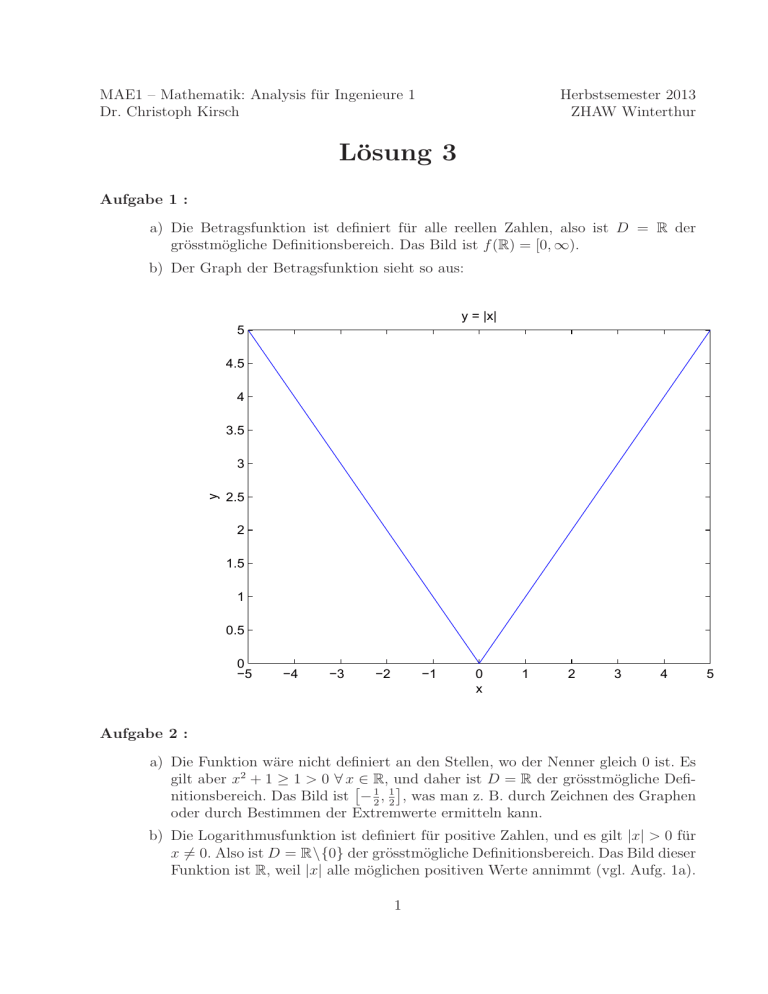
b) Der Graph der Betragsfunktion sieht so aus:
y = |x|
5
4.5
4
3.5
y
3
2.5
2
1.5
1
0.5
0
−5
−4
−3
−2
−1
0
x
1
2
3
4
Aufgabe 2 :
a) Die Funktion wäre nicht definiert an den Stellen, wo der Nenner gleich 0 ist. Es
gilt aber x2 + 1 ≥ 1 > 0 ∀ x∈ R, und
daher ist D = R der grösstmögliche Definitionsbereich. Das Bild ist − 21 , 21 , was man z. B. durch Zeichnen des Graphen
oder durch Bestimmen der Extremwerte ermitteln kann.
b) Die Logarithmusfunktion ist definiert für positive Zahlen, und es gilt |x| > 0 für
x 6= 0. Also ist D = R\{0} der grösstmögliche Definitionsbereich. Das Bild dieser
Funktion ist R, weil |x| alle möglichen positiven Werte annimmt (vgl. Aufg. 1a).
1
5
c) Die Wurzelfunktion ist definiert für nichtnegative Argumente, also muss
1
g(x) := x2 − x − 3 ≥ 0
2
(1)
gelten. Der Graph der Funktion g ist eine Parabel mit negativen Werten zwischen
den beiden Nullstellen. Diese sind gegeben durch
q
1
1
±
+ 12
1 7
3
2
4
x1,2 =
= ± ∈ − ,2 .
(2)
2
4 4
2
Im Bereich zwischen diesen
Nullstellen ist die Funktion f nicht definiert, und
3
daher ist D = −∞, − 2 ∪ [2, ∞) der grösstmögliche Definitionsbereich. Weil
die Funktion g in diesem Bereich alle möglichen nichtnegativen Werte annimmt,
ist das Bild gegeben durch f (D) = [0, ∞).
Zur Veranschaulichung zeichnen wir zusätzlich die Graphen der drei Funktionen:
y = x/(x2+1)
0.5
0.4
0.3
0.2
y
0.1
0
−0.1
−0.2
−0.3
−0.4
−0.5
−5
−4
−3
−2
−1
0
x
2
1
2
3
4
5
y = log|x|
2
1.5
1
0.5
y
0
−0.5
−1
−1.5
−2
−2.5
−3
−5
−4
−3
−2
−1
0
x
y=
r
1
2
3
4
5
2
3
4
5
1
x2 − x − 3
2
5
4.5
4
3.5
y
3
2.5
2
1.5
1
0.5
0
−5
−4
−3
−2
−1
0
x
3
1
Aufgabe 3 :
Wir lösen zunächst die Gleichung nach y auf und erhalten
y=
1
.
|x − 1|
(3)
Diese Funktion ist definiert für x 6= 1, also ist D = R \ {1} der grösstmögliche
Definitionsbereich. Für den Graphen erhalten wir
y = 1/|x−1|
10
9
8
7
y
6
5
4
3
2
1
0
−5
−4
−3
−2
−1
4
0
x
1
2
3
4
5
Aufgabe 4 :
Wir zeichnen die in der Wertetabelle gegebenen Punkte und verbinden sie mit Linien:
I(U)
80
60
40
I [Am−2]
20
0
−20
−40
−60
−80
−2
−1.5
−1
−0.5
0
0.5
U [V]
Für Anwendungen ist vor allem der Bereich zwischen der Kurzschlusspannung U =
0 und der Leerlaufspannung I(U ) = 0 interessant; in diesem Bereich sollten mehr
Messungen durchgeführt werden.
Vorlesungswebseite: http://home.zhaw.ch/~kirs/MAE1
5