1111011 pos + pos

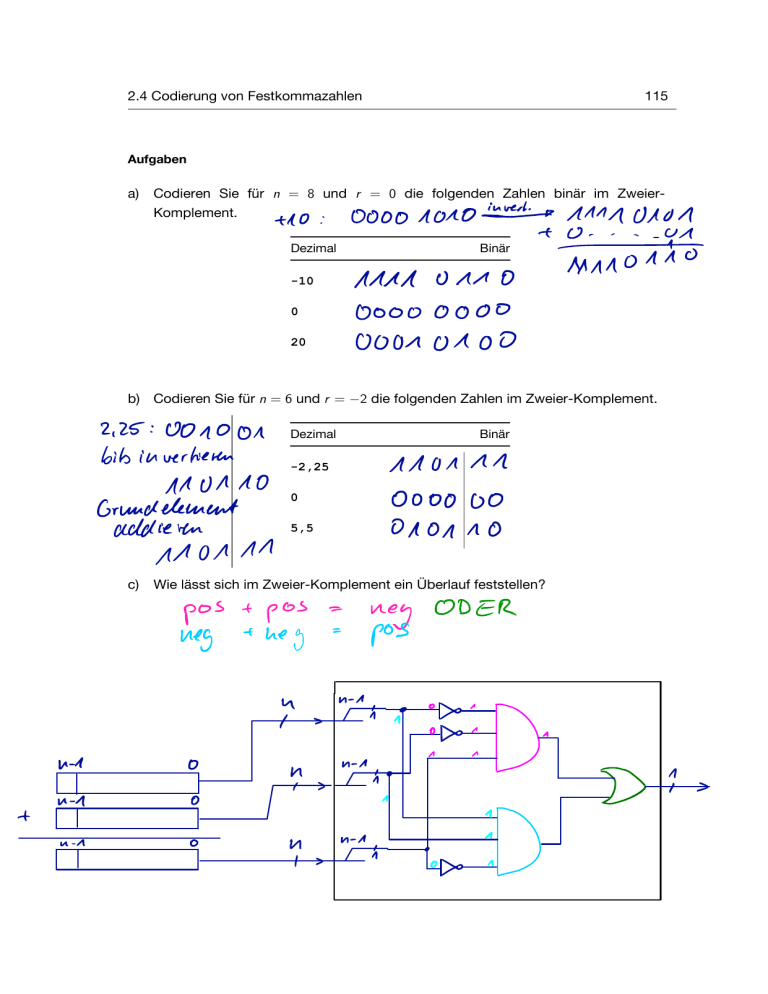
2.4 Codierung von Festkommazahlen
115
Aufgaben
Codieren Sie für n = 8 und r = 0 die folgenden Zahlen binär im Zweier.EC
Komplement.
11110101
00001010
:
+10
a)
+
Dezimal
Binär
1111
-10
0
00000000
20
00010100
b) Codieren Sie für n = 6 und r =
2,25
bibin
001001
:
0110
110110
Grundelement
addieren
-2,25
110111
0
000000
+
pos
+
neg
=
n
|
1
-
"
s
1)]
o/\o
.
1
o
^
0
-1
n
n
/
in
s
#
"
1
n
O/\o
.
1
0
1
+
u
-1
1111011
ODER
neg
pos
=
h
-1
-
Wie lässt sich im Zweier-Komplement ein Überlauf feststellen?
neg
n
ch
.
010110
5,5
pos
n -1
.
Binär
110111
c)
.
2 die folgenden Zahlen im Zweier-Komplement.
Dezimal
vertreten
0
O
n
U
|
>
-
1g
•
1
-
21
/
s
0110
+
0011
10011100
1111
1111
99
+156
255
116
2 Darstellung von Zahlen und Zeichen
d) Berechnen Sie 37 - 53 im Zweier-Komplement für n = 8, r = 0.
37
53
-53
-53
=
>
37T
=
0011
(
-
53
)
0101
11001011
37=+001991011
11110000
C
=
-16
)
118
2 Darstellung von Zahlen und Zeichen
2.5 Codierung von Gleitkommazahlen nach IEEE 754
Durch die fest definierte Kommastelle sind bei Festkommazahlen die Abstände zwischen
den einzelnen Zahlenwerten äquidistant. Aus diesem Grund (und aufgrund der endlichen
Anzahl an Stellen n) können mit Festkommazahlen nicht gleichzeitig sehr große Zahlen
und sehr kleine Zahlen dargestellt werden.
Bei Gleitkommazahlen ist diese Einschränkung aufgehoben. Die Abstände zwischen den
einzelnen Zahlenwerten sind um den Wert 0 herum sehr klein. Für große Zahlen werden
die Abstände sehr groß, wie in nachstehender Grafik skizziert.
0
Erreicht wird diese Eigenschaft dadurch, dass die Position des Kommas nicht im Voraus
festgelegt ist, sondern in der Zahl durch Angabe eines Exponenten e definiert wird.
Der Exponent legt fest, um wieviel die Kommastelle nach links oder rechts verschoben
werden muss.
Gleitkommazahlen werden wie folgt codiert:
s
e
f
Bei 32 Bit breiten Gleitkommazahlen (einfache Genauigkeit) gilt die Aufteilung
• s = 1 Bit
• e = 8 Bit
• f = 23 Bit,
bei 64 Bit breiten Gleitkommazahlen (doppelte Genauigkeit) gilt die Aufteilung
• s = 1 Bit
• e = 11 Bit
• f = 52 Bit.
Als Wert ergibt sich für
• für normalisierte Gleitkommazahlen (Normal-Fall) v = ( 1)s · 1,f · 2e
K,
• für de-normalisierte Gleitkommazahlen (Spezial-Fall) v = ( 1)s · 0,f · 21
K.
2.5 Codierung von Gleitkommazahlen nach IEEE 754
119
Die Konstante K hat
• bei einfacher Genauigkeit (32 Bit) den Wert K = 127,
• bei doppelter Genauigkeit (64 Bit) den Wert K = 1023.
Eine Gleitkommazahl gilt als normalisiert, wenn beim Exponenten e weder alle Bits
gesetzt noch alle Bits gelöscht sind, d.h.
• 0 < e < 255 bei 32 Bit
• 0 < e < 2047 bei 64 Bit.
Eine denormalisierte Gleitkommazahl liegt vor, wenn e = 0 und gleichzeitig f > 0.
Spezialfälle:
• 0:
• e=0
• f =0
• ±1:
• s: +1 ) 0;
1)1
• e: alle Bits gesetzt ) 255 bei 32 Bit, 2047 bei 64 Bit
• f: alle Bits 0
• NaN (Not a Number)
• e: alle Bits gesetzt ) 255 bei 32 Bit, 2047 bei 64 Bit
• f: > 0
Aufgaben
Format von Gleitkommazahlen
a)
Welchen Wert hat eine Zahl, die in 64 Bit Gleitkomma-Notation mit
0xC028000000000000 codiert wird?
63
62
52
000000101000
1100
⇒
1,1
-
=
-
.
1
21026-1023
100,00
.
=
-
=
.
1.1.23
-12
.
120
2 Darstellung von Zahlen und Zeichen
b) Welchen Wert hat eine Zahl, die in 64 Bit Gleitkomma-Notation mit
0x0004000000000000 codiert wird?
010100
0,25
=
c)
.
.
.
.
21
-
k
21-1023
.
Welchen Wert hat eine Zahl, die in 32 Bit Gleitkomma-Notation mit 0x7F80000
codiert wird?
d) Was ist eine denormalisierte Gleitkommazahl, wie wird sie codiert und wie berechnet sich ihr Wert?
e)
Welchen Nutzen haben denormalisierte Gleitkommazahlen?
statt
0,11,1
(
f)
um
0
herum
⇒
)
sehr
kleine
Werk
darstellen
Geben Sie ein Beispiel an, wie es zu einem Ergebnis kommen kann, das ‘‘keine
Zahl’’ ist.
2.5 Codierung von Gleitkommazahlen nach IEEE 754
121
Rechnen mit Gleitkommazahlen
a)
Codieren Sie 3,625 und 13,5 als 32 Bit breite Gleitkommazahlen und tragen Sie
das Bitmuster in die angegebene Tabelle ein.
3,625
=
,
I
k=1
e-
e-
k
1+127=128
1101,12=1,1011-23
l
13,5W
=
1T
k
=
=
11,1012=1,111.219
e-
K
es
=3
Itk
3+127=130
=
128+2
=
01000001010110
3,625:
13,5:
01000000011010
.
-
.
-
.
-
.
0
0
122
2 Darstellung von Zahlen und Zeichen
b) Berechnen Sie 3,625 + 13,5 im Binärsystem bei Verwendung einer 32 Bit Gleitkommacodierung.
Exponent
gemeinsamer
bei
⇒
(
⇒
⇒
3,625
auf
Exponent
Man fisse
13,5
3,625
von
:
3,625
1
10
1000
:
2
um
)
0010
Stellen
1
11
110000
111010
0
1^0.6
01110
"
.
0h00
0
]
0
0
1
.
.
000
01
0
+
anpassen
schieben
rechts
:
130
Exponent
gemeinsamer
nach
130
:
2
0
0
schieben
1
um
schieben
1
um
0
10
Pujo
Renormalize
,
statt
1
⇒
,
1
um
stelle
Hdrts
sdüeben
Exponent
⇒
1,00010010
nach
.
-
und
1
um
.
um
Exponent
f
:
130+1--131=128+3
Bitmuster des Ergebnisses:
0
1000
0011
00010010
.
-
0
dafür
erhöhen
2.5 Codierung von Gleitkommazahlen nach IEEE 754
c)
T
123
Bestimmen Sie aus dem Ergebnis-Bitmuster das Ergebnis der Addition 3,625 +
13,5
d) Codieren Sie 1,75 und 5,125 als 64 Bit breite Gleitkommazahlen und tragen Sie
das Bitmuster in die angegebene Tabelle ein.
1,75
5,125
124
T
e)
2 Darstellung von Zahlen und Zeichen
Berechnen Sie 1,75 + 5,125 im Binärsystem bei Verwendung einer 64 Bit Gleitkommacodierung.
Bitmuster des Ergebnisses:
2.5 Codierung von Gleitkommazahlen nach IEEE 754
T
f)
125
Bestimmen Sie aus dem Ergebnis-Bitmuster das Ergebnis der Addition 1,75 +
5,125
126
2 Darstellung von Zahlen und Zeichen