2.5 Codierung von Gleitkommazahlen nach IEEE 754
Werbung

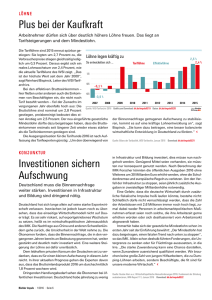
118 2 Darstellung von Zahlen und Zeichen 2.5 Codierung von Gleitkommazahlen nach IEEE 754 Durch die fest definierte Kommastelle sind bei Festkommazahlen die Abstände zwischen den einzelnen Zahlenwerten äquidistant. Aus diesem Grund (und aufgrund der endlichen Anzahl an Stellen n) können mit Festkommazahlen nicht gleichzeitig sehr große Zahlen und sehr kleine Zahlen dargestellt werden. Bei Gleitkommazahlen ist diese Einschränkung aufgehoben. Die Abstände zwischen den einzelnen Zahlenwerten sind um den Wert 0 herum sehr klein. Für große Zahlen werden die Abstände sehr groß, wie in nachstehender Grafik skizziert. 0 : Erreicht wird diese Eigenschaft dadurch, dass die Position des Kommas nicht im Voraus festgelegt ist, sondern in der Zahl durch Angabe eines Exponenten e definiert wird. Der Exponent legt fest, um wieviel die Kommastelle nach links oder rechts verschoben werden muss. Gleitkommazahlen werden wie folgt codiert: s e f Bei 32 Bit breiten Gleitkommazahlen (einfache Genauigkeit) gilt die Aufteilung • s = 1 Bit • e = 8 Bit • f = 23 Bit, bei 64 Bit breiten Gleitkommazahlen (doppelte Genauigkeit) gilt die Aufteilung • s = 1 Bit • e = 11 Bit • f = 52 Bit. Als Wert ergibt sich für • für normalisierte Gleitkommazahlen (Normal-Fall) v = ( 1)s · 1,f · 2e K, • für de-normalisierte Gleitkommazahlen (Spezial-Fall) v = ( 1)s · 0,f · 21 K. 2.5 Codierung von Gleitkommazahlen nach IEEE 754 119 Die Konstante K hat • bei einfacher Genauigkeit (32 Bit) den Wert K = 127, • bei doppelter Genauigkeit (64 Bit) den Wert K = 1023. Eine Gleitkommazahl gilt als normalisiert, wenn beim Exponenten e weder alle Bits gesetzt noch alle Bits gelöscht sind, d.h. • 0 < e < 255 bei 32 Bit • 0 < e < 2047 bei 64 Bit. Eine denormalisierte Gleitkommazahl liegt vor, wenn e = 0 und gleichzeitig f > 0. Spezialfälle: • 0: • e=0 • f =0 • ±1: • s: +1 ) 0; 1)1 • e: alle Bits gesetzt ) 255 bei 32 Bit, 2047 bei 64 Bit • f: alle Bits 0 • NaN (Not a Number) • e: alle Bits gesetzt ) 255 bei 32 Bit, 2047 bei 64 Bit • f: > 0 Aufgaben Format von Gleitkommazahlen a) Welchen Wert hat eine Zahl, die in 64 Bit Gleitkomma-Notation mit 0xC028000000000000 codiert wird? 2.5 Codierung von Gleitkommazahlen nach IEEE 754 c) Bestimmen Sie aus dem Ergebnis-Bitmuster das Ergebnis der Addition 3,625 + 13,5 227 137 ( .n)° T 0 . . . 123 100.07001 - 2 . qooon = ,oon 17,125W 20£ - d) Codieren Sie 1,75 und 5,125 als 64 Bit breite Gleitkommazahlen und tragen Sie das Bitmuster in die angegebene Tabelle ein. an i 01,22920 : a 200 O = e - 2025=0 C = fs 1023 770 @= X One 27 -2 J , 12J ,ot e - 104,00^9.0 U=2 e- V 1,75 5,125 20 1,0^0020--0.2 = → 2023=2 e - - 2025 f 2212717 0 . 70000000001 27 ^ n7O on . . . . 0020 O . . . d . . ,1 124 T e) 2 Darstellung von Zahlen und Zeichen Berechnen Sie 1,75 + 5,125 im Binärsystem bei Verwendung einer 64 Bit Gleitkommacodierung. 7,75N Expo 01729277777 125 ÷ ÷ . 2-20 Martine 1,190 . - . ' 0 . 90,2007° → " 0000001 00000008 zoo 6 " ,•o non 700 7in 2,010070 no 2177227727 W 0,7170 2.40 . - 0020 ? - Mainline µj✓ 0 10000000002 n.ee ' zorro . O ¢ . Bitmuster des Ergebnisses: 1000000000 . , + 0 - . . C - . ° - ' :O . .r21o÷ Exponent 0 3 ( Montrose Expo . . . 0 . d n.f.ae 2.5 Codierung von Gleitkommazahlen nach IEEE 754 T f) ( 125 Bestimmen Sie aus dem Ergebnis-Bitmuster das Ergebnis der Addition 1,75 + 5,125 , )° iwip 2 . 7 7022^-2 , . = + 025-7023 a Z=X 770 , 217 c- ±6c87J - oz , , 132 3 Arithmetische Schaltungen Speicherelemente: Flipflops und Register Wenn man zwei Inverter rückgekoppelt zusammenschließt, so dass der Ausgang des einen Inverters mit dem Eingang des anderen Inverters verbunden ist, lässt sich ein einzelnes Bit speichern. y Der Wert des gespeicherten Bits ist jedoch nicht veränderbar. Um einen bestimmten Wert abzuspeichern, muss die Rückkopplung an einer Stelle aufgelöst werden und der abzuspeichernde Wert angelegt werden. 01 a Verwendet man Logik-Bauteile mit mehr als zwei Eingängen (NICHT-ODER (NOR), NICHT-UND (NAND), kann auf die Unterbrechung der Rückkopplung verzichtet werden. 2 b % ¢=7 a1 a2 x y y a1 a2 y 0 0 1 1 0 1 0 1 1 0 0 0 Nachstehende Tabelle zeigt eine Änderung der Eingangswerte der rückgekoppelten NOR-Schaltung über der Zeit. Zum Zeitpunkt t1 wird Eingang a auf 1 gelegt, zum Zeitpunkt t2 wieder auf 0. ⌧ ist die Gatterlaufzeit. a) , ^ y a *: abl Ers Tragen Sie in die Tabelle die zu den jeweiligen Zeiten gehörenden Ausgangswerte x und y ein. t 0 t1 t1 + ⌧ t1 + 2⌧ t1 + 3⌧ ... t2 t2 + ⌧ ... a 0 1 1 1 1 ... 0 0 ... b 0 0 0 0 0 ... 0 0 ... x ? ? 0 0 0 ... 0 0 ... y ? ? ? 1 1 ... 1 1 ... a n 0 140 3 Arithmetische Schaltungen Komplement identische Bewegungen auf dem Zahlenring identische Wertänderungen zur Folge haben, liefert die Ripple-Carry-Schaltung nicht nur bei vorzeichenlose Festkommazahlen korrekte Ergebnisse, sondern auch bei vorzeichenbehafteten Zahlen im Zweier-Komplement. (Das gilt jedoch nur, wenn keine Überläufe auftreten.) Die Ripple-Carry-Schaltung kann also nicht nur addieren, sondern auch subtrahieren. Dazu muss der zu subtrahierenden Wert zunächst negiert (Vorzeichen ändern) und anschließend addiert werden: x y = x + ( y ). b) Tragen Sie in nachstehende Schaltung Verbindungslinien und Schaltungselemente ein, so dass die Ripple-Carry-Schaltung nicht nur addieren sondern auch subtrahieren kann. xn-1 yn-1 xi yi ci-1 si sn-1 c) x1 y2 … VA ci x2 … y1 im xi ci-1 xi VA … ci … pp yi x0 si s2 p yi y0 ci-1 xi VA ci yi ci-1 VA si s1 ci Pp si s0 Zeichnen Sie in obige Ripple-Carry-Schaltung den kritischen Pfad ein. Wieviele Gatterlaufzeiten ⌧ benötigt die Ripple-Carry-Schaltung zur Subtraktion zweier n Bit breiter Festkommazahlen? Wieviel im Fall n = 64? 3.5 Carry-Look-Ahead 145 Kaskadierung von Carry-Look-Ahead-Schaltungen Mit einer Kaskadierung kann der mit großer Wortbreite einhergehenden großen Anzahl an Gattern entgegengewirkt werden. Dazu werden Carry-Look-Ahead-Schaltungen hoher Wortbreite aus mehreren Carry-Look-Ahead-Schaltungen niedrigerer Wortbreite zusammengesetzt. Nachfolgende Abbildung zeigt eine Erweiterung der bekannten 4 Bit Carry-Look-Ahead-Schaltung zur Ausgabe von Generate- und Propagate-Signalen. x y 3 2 3 0 1 3 2 1 0 0 2 1 1 0 1 0 1 0 0 1 G inv g3 p3 g2 p2 g1 p1 g0 p0 . x3 y3 c2 x2 VA c3 P y2 c1 x1 VA s3 c2 3 y1 c0 x0 VA s2 c1 VA s1 2 y0 c-1 c0 s0 1 C 0 s Zur Zusammenfassung mehrerer Carry-Look-Ahead-Schaltungen werden die Generate/Propagate-Signale mit einer sog. Carry-Look-Ahead-Einheit verbunden. 4 4 4 4 4 4 4 4 CLA CLA CLA CLA 4 4 4 4 1 x y inv. s G3P3 C3 G2P2 C2 G1P1 C1 G0P0 C0 Carry-Look-Ahead-Einheit GG0 PP0 CC0 150 3 Arithmetische Schaltungen a T j) Skizzieren Sie für Fan-In = 2 eine Gatterschaltung zur Bestimmung von C3 . Zeichnen Sie den kritischen Pfad ein und bestimmen Sie die maximale Anzahl an Gatterlaufzeiten ⌧ . = 6 , ✓ ( R 6,1 n u ( R Caa ✓ ( Pz n R n Po R r n n ←*€⇐¥±÷ei¥ of &TkE - of Yeo , Nehmen Sie die für Fan-In = 4 bestimmten Gatterlaufzeiten an, vgl. c), f), g). k) Bestimmen Sie die maximale Gatterlaufzeit der zweistufigen 16 Bit Carry-LookAhead-Schaltung zur korrekten Bestimmung von s. l) Bestimmen Sie die maximale Gatterlaufzeit der zweistufigen 16 Bit Carry-LookAhead-Schaltung zur korrekten Bestimmung von PP0 . 6 ) . 3.5 Carry-Look-Ahead 151 m) Bestimmen Sie die maximale Gatterlaufzeit der zweistufigen 16 Bit Carry-LookAhead-Schaltung zur korrekten Bestimmung von GG0 . → Zx ( mat = 2660=82 : ,y )p 6) Zxy €6 + → , I = o ,P -766 : not , . . . , Nachfolgende Abbildung zeigt eine dreistufige Carry-Look-Ahead-Schaltung zur Verarbeitung von 64 Bit breiten Zahlen. x 64 CLA-Einheit d GG3 PP3 CLA-Einheit c CC3 GG2 PP2 y 64 add/sub CLA-Einheit b CC2 GG1 PP1 CC1 CLA-Einheit a GG0 PP0 CC0 CLA-Einheit e CC4 ÜberlaufErkennung Cca 64 t⇐⇐€µz⇐Eh H C#¥p s n) Bestimmen Sie die max. Gatterlaufzeit zur Berechnung von CC3 für Fan-In = 4. - 662 ✓ - Bi 7 a a ✓ ( PP co → 82 e.at : , ( PRN 6,6 NPP , rppon , 2¥ UND - ODER ) VCPRNPR Eco ) n66o ) gppo 5 , 7 G⇒p÷ Pc . 6aH✓ 662