Mathematische Methoden I (WS 16/17)

Mathematische Methoden I (WS 16/17)
Grundlagen
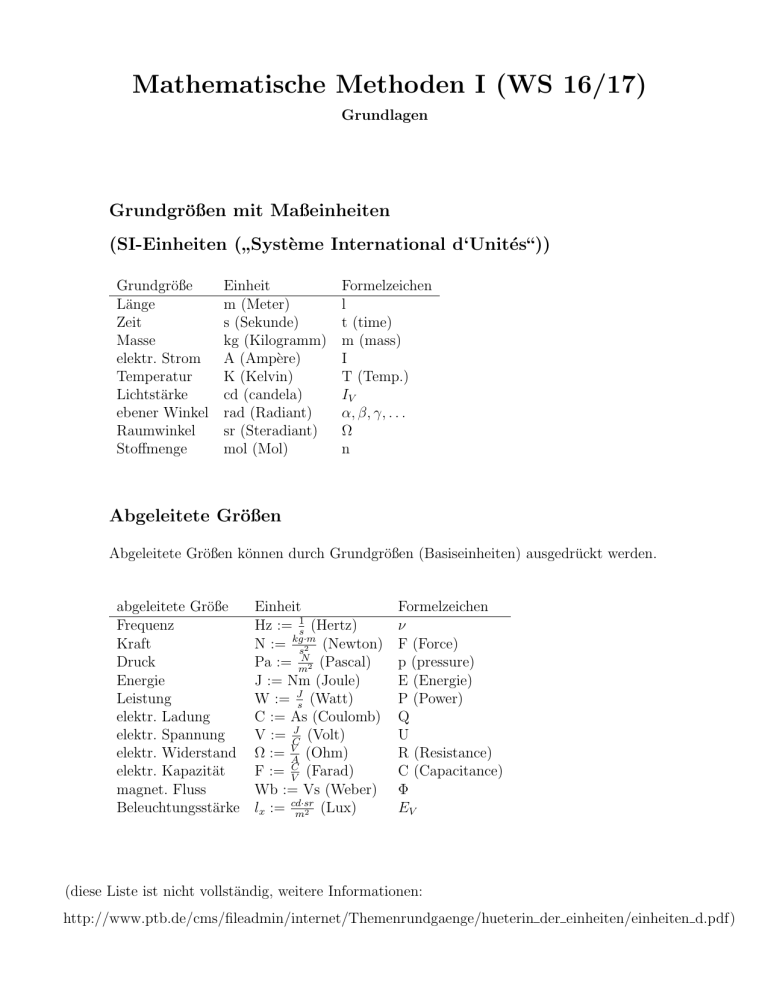
Grundgrößen mit Maßeinheiten
(SI-Einheiten ( Système International d‘Unités“))
”
Grundgröße
Länge
Zeit
Masse
elektr. Strom
Temperatur
Lichtstärke
ebener Winkel
Raumwinkel
Stoffmenge
Einheit
m (Meter)
s (Sekunde)
kg (Kilogramm)
A (Ampère)
K (Kelvin)
cd (candela)
rad (Radiant)
sr (Steradiant)
mol (Mol)
Formelzeichen
l
t (time)
m (mass)
I
T (Temp.)
IV
α, β, γ, . . .
Ω
n
Abgeleitete Größen
Abgeleitete Größen können durch Grundgrößen (Basiseinheiten) ausgedrückt werden.
abgeleitete Größe
Frequenz
Kraft
Druck
Energie
Leistung
elektr. Ladung
elektr. Spannung
elektr. Widerstand
elektr. Kapazität
magnet. Fluss
Beleuchtungsstärke
Einheit
Hz := 1s (Hertz)
N := kg·m
(Newton)
s2
Pa := mN2 (Pascal)
J := Nm (Joule)
W := Js (Watt)
C := As (Coulomb)
V := CJ (Volt)
Ω := VA (Ohm)
F := VC (Farad)
Wb := Vs (Weber)
lx := cd·sr
(Lux)
m2
Formelzeichen
ν
F (Force)
p (pressure)
E (Energie)
P (Power)
Q
U
R (Resistance)
C (Capacitance)
Φ
EV
(diese Liste ist nicht vollständig, weitere Informationen:
http://www.ptb.de/cms/fileadmin/internet/Themenrundgaenge/hueterin der einheiten/einheiten d.pdf)
Griechisches Alphabet
alpha
beta
gamma
delta
epsilon
zeta
eta
theta
iota
kappa
lambda
my
α
β
γ
δ
ε, ζ
η
ϑ, θ
ι
κ, κ
λ
µ
A
B
Γ
∆
E
Z
H
Θ
I
K
Λ
M
ny
xi
omikron
pi
rho
sigma
tau
ypsilon
phi
chi
psi
omega
ν
ξ
o
π, $
ρ, %
σ, ς
τ
υ
ϕ, φ
χ
ψ
ω
N
Ξ
O
Π
P
Σ
T
Υ
Φ
X
Ψ
Ω
Größenordnungen (Abkürzungen für Zehnerpotenzen)
1
= 10−1
Zehntel
10
1
= 10−2
Hundertstel 100
1
Tausendstel 1000 = 10−3
1
Millionstel
= 10−6
1000000
−9
Milliardstel 10
Billionstel
10−12
Billiardstel 10−15
Zehn
Hundert
Tausend
Million
Milliarde
Billion
Billiarde
10 = 101
100 = 102
1000 = 103
1000000 = 106
109
1012
1015
d
c
m
µ
n
p
f
DeziZentiMilliMikroNanoPicoFemto-
D Dekah Hektok KiloM MegaG GigaT TeraP Peta-
Mathematische Zeichen
+
·
/
=
6
=
≡
<
>
≤
≥
±
∼
≈
∞
P
plus
minus
mal
geteilt durch
gleich
ungleich
identisch gleich
kleiner als
größer als
kleiner oder gleich
größer oder gleich
klein gegen
Q
!
:
:=
⊥
=
b
groß gegen
plus oder minus
proportional zu
ungefähr gleich
unendlich“
”
Summenzeichen
Produktzeichen
Fakultätszeichen
sodass
definiert durch
steht senkrecht auf
entspricht
Beispiele für Summe, Produkt, Fakultät
3
P
i=1
n
P
i=1
3
Q
ai = a1 + a2 + a3
i = 1 + 2 + 3 + ... + n = n2 (n + 1) (Gauß)
ai = a1 · a2 · a3
i=1
n! := 1 · 2 · 3 · ...(n − 1) · n =
n
Q
i=1
i und Konvention 0! = 1
logische Zeichen
Zeichen Bedeutung
∈
Element von
3
enthält als Element
∈
/
kein Element von
⊆
Untermenge von ... oder gleich
⊇
enthält als Untermenge ... oder ist gleich
∪
Vereinigungsmenge
∩
Durchschnittsmenge
∅
Nullmenge
\
ohne
∃
es existiert
∀
für alle
⇒
daraus folgt (ist hinreichende Bedingung für...)
⇐
gilt wenn (ist notwendige Bedingung für...)
⇔
gilt genau dann, wenn (ist notw. und hinr. Bedingung für...)
∨
oder
∧
und
¬
nicht
Beispiele
A ⇒ B bedeutet “aus A folgt B”
oder “A ist hinreichend für B”
oder “B ist notwendig für A”
B ⇒ A analog
A ⇔ B bedeutet: (A ⇒ B) ∧ (B ⇒ A)
Beispiele für logische Äquivalenzen
¬ (A ∧ B) ≡ (¬A ∨ ¬B) (Gesetz von Morgan)
((A ∧ B) ∨ C)≡ ((A ∨ C) ∧ (B ∨ C)) (Distributivgesetz)
(A ∧ (B ∧ C)) ≡ ((A ∧ B) ∧ C) (Assoziativgesetz)
Zahlen
i) Natürliche Zahlen: N := {1, 2, 3, ...}
Natürliche Zahlen und neutrales Element: N0 := N ∪ {0} = {0, 1, 2, 3, ...}
ii) Ganze Zahlen: Z := N ∪ {0}
 ∪ {−a | a ∈ N} = {0, 1, −1, 2, −2, ...}

a
;a ≥ 0
)
(Einschub: Betrag: |a| =

−a ; a < 0
o
n
iii) Rationale Zahlen(=”Brüche”): Q := pq | p ∈ Z & q ∈ Z \ {0}
√
(Nebenbemerkung: 2 ∈
/ Q)
iv) Reelle Zahlen: R
R entspricht der Menge aller Punkte der Zahlengeraden
v) Komplexe Zahlen: Cy später
Beweisverfahren
i) Direkter Beweis
Die zu beweisende Aussage ist von der Form A ⇒ B. Annahme: A ist wahr, folgere
daraus, dass B wahr ist.
Beispiel:
Es sei a eine ganze Zahl. Zeige (6 | a) ⇒ (3 | a) .
(Notation: (b | a) bedeutet “a ist teilbar durch b”, oder “es existiert eine ganze Zahl k
mit a = k · b.)
Direkter Beweis: (6 | a) ⇒ ∃k, so dass a = 6 · k = (3 · 2) · k = 3 · (2 · k)
| {z }
=:k̃
⇒ ∃k̃,so dass a = 3 · k̃ ⇒ (3 | a). ii) Beweis durch Umkehrschluss
Äquivalenz: (A ⇒ B) ≡ (¬B ⇒ ¬A)
Annahme: ¬B ist wahr, folgere daraus, dass ¬A wahr ist.
Beispiel:
Es sei T, m, n ∈ N. Ist eine der Zahlen m, n nicht durch T teilbar, dann sind auch
m − n oder m + n nicht teilbar durch T .
Zuerst drücken wir diese Aussage in Form mathematischer Logik aus:
m
n
n
m+n
m−n
∈
/ N∧ ∈N ∨
∈N∧ ∈
/N ⇒
∈
/ N∨
∈
/ N.
T
T
T
T
T
T
m
Der Umkehrschluss dieser Aussage lautet
¬
h m
m
i
m+n
m−n
n
n
∈
/ N∨
∈
/N
⇒ ¬
∈
/ N∧ ∈N ∨
∈N∧ ∈
/N
T
T
T
T
T
T
m
m
m−n
n
n
m+n
∈N∧
∈N ⇒
∈N∨ ∈
/N ∧
∈
/ N∨ ∈N
T
T
T
T
T
T
m
m
m+n
m−n
n
n
∈N∧
∈N ⇒
∈N∧ ∈N ∨
∈
/ N∧ ∈
/N
T
T
T
T
T
T
wobei wir das Gesetz von Morgan verwendet haben, sowie, dass
(A ∨ ¬B) ∧ (¬A ∨ B) ≡ (A ∧ B) ∨ (¬A ∧ ¬B)
gilt, was man leicht anhand einer Wahrheitstabelle überprüfen kann.
m+n
T
Diese Aussage können wir direkt beweisen. Die linksseitige Bedingung liefert
z1 und
m−n
T
= z2 , wobei z1 , z2 ∈ N. Wenn wir uns die Teiler
m
T
= r1 sowie
n
T
=
= r2
anschauen erhält man r1 + r2 = z1 . Nun kann die Summe zweier Zahlen nur eine ganze
Zahl liefern, falls beide Zahlen, d.h. r1 und r2 beide ganzzahlig sind, oder beide nichtganzzahlig sind. Das Gleiche gilt für die Differenz. D.h. entweder sind beide teilbar
durch T oder weder m noch n ist teilbar durch T , was unsere Aussage beweist.
iii) Beweis durch Widerspruch (indirekter Beweis)
Zu beweisen ist, dass eine Aussage wahr ist. Annahme: die Aussage ist falsch; führe
diese Aussage zum Widerspruch.
Beispiel:
Satz :
√
2 ist irrational.
Beweis: Annahme:
√
2 ist rational, d.h. ∃ teilerfremde a, b ∈ Z, so dass
2b2 = a2 ⇒ a2 ist gerade ⇒ a ist gerade ⇒ ∃c ∈ Z, so dass a = 2c
⇒ 2b2 = |{z}
4c2 ⇒ b2 = 2c2 ⇒ b ist gerade ⇒ 2 ist Teiler von a und b
=a2
WIDERSPRUCH!
√
2=
a
b
⇒
iv) vollständige Induktion
Es sei A(n) eine Aussage, die von n ∈ N abhängt.
1. Induktionsanfang: zeige A(1)
2. Induktionsannahme: A(n) gilt für n
3. Induktionsschluss: zeige, dass ∀n ∈ N gilt: A(n)⇒ A(n + 1)
Daraus folgt A(n) für alle n.
Beispiel:
Es sei zu zeigen, dass
n
P
(4k − 3) = n (2n − 1) ∀n ∈ N
k=1
1. Induktionsanfang: zu zeigen, dass die Behauptung für n=1 gilt.
n=1
LHS = 4 − 3 = 1
RHS = 1 · (2 − 1) = 1
√
2. Induktionsannahme: s.o.
3. Induktionsschluss: zu zeigen ist A(n) ⇒ A(n + 1), d.h es muss unter Benutn+1
P
zung der Induktionsannahme A(n) gezeigt werden dass gilt:
(4k − 3) =
k=1
(n + 1) (2 (n + 1) − 1)
n
P
LHS =
(4k − 3) + 4(n + 1) − 3 = n(2n − 1) + 4(n + 1) − 3=2n2 + 3n + 1
k=1
↑
Ind.ann.
RHS = 2(n + 1)2 − (n + 1)=2n2 + 3n + 1 = LHS
⇒die Behauptung gilt für alle n,
q.e.d.