3.6 Addition und Subtraktion von Gleitkommazahlen 3.7
Werbung

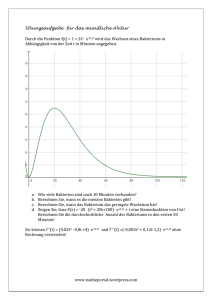
3.7 Kombinatorischer Multiplizierer 137 3.6 Addition und Subtraktion von Gleitkommazahlen Zur Addition von Gleitkommazahlen wird auf Festkomma-Addierer und -Subtrahierer zurückgegriffen. Zwei positive Gleitkommazahlen können wie folgt addiert werden: • Als Exponent des Ergebnisses wird der größere Exponent verwendet • Bilden der Differenz der beiden Exponenten • Mantisse der Zahl mit dem kleineren Exponenten zusammen mit der führenden ‘‘1,’’ um die zuvor berechnete Differenz nach rechts schieben • Beide Mantissen addieren • Falls Ergebnis nicht in Form ‘‘1,...’’ ist, Mantisse um 1 Stelle nach rechts schieben und 1 zum Ergebnis-Exponenten addieren (= Re-Normalisieren) Um Gleitkommazahlen zu subtrahieren, kann wie oben vorgegangen werden, wenn der Subtrahend negiert wird. Das gleiche gilt für die Addition von Zahlen unterschiedlichen Vorzeichens. 3.7 Kombinatorischer Multiplizierer Bei der Multiplikation gilt allgemein: Multiplikator · Multiplikand = Produkt Mit Multiplikator x und Multiplikand y berechnet sich bei vorzeichenlosen Zahlen das Produkt z zu: x3 + + + = z7 x2 x 3 · y3 z6 x1 x0 x2 · y 3 x3 · y 2 z5 x1 · y3 x2 · y2 x3 · y1 z4 · y3 x 0 · y3 x 1 · y2 x 2 · y1 x 3 · y0 z3 y2 x0 · y 2 x1 · y 1 x2 · y 0 y1 x0 · y1 x1 · y0 y0 x 0 · y0 z2 z1 z0 Die Multiplikation zweier n Ziffern breiter Zahlen ergibt ein 2n breites Produkt. Das Produkt berechnet sich als Summe von n Teilprodukten. Die Multiplikation der Einzel-Terme xi · yj entspricht einer logischen UND-Verknüpfung. Die Addition der Teilprodukte xi · yj kann mit Halb- und Volladdierern durchgeführt werden. 138 a) 3 Arithmetische Schaltungen Tragen Sie in nachfolgende Abbildung Verbindungen zur Realisierung der vorzeichenlosen Multiplikation ein. x3 Eigene Lösung: x3 + + + = x2 z7 x1 x2 x1 x0 x 3 · y3 z6 x2 · y 3 x3 · y 2 z5 x1 · y3 x2 · y2 x3 · y1 z4 x0 y3 · y · y3 x 0 · y3 x 1 · y2 x 2 · y1 x 3 · y0 z3 y2 y2 x0 · y 2 x1 · y 1 x2 · y 0 y1 x0 · y1 x1 · y0 y0 x 0 · y0 z2 z1 z0 y1 3 y0 2 1 x0 y 3 2 1 0 x1 ⌧ a b a HA cout 3 b cin a VA ⌧ cout s y 2 b VA cout s 1 cin a 2⌧ s cout 0 x2 a cin b a 3 cin a cout s 2 cin VA cout s y 1 b 3⌧ VA 2⌧ VA ⌧ cout b a b HA cout s s 0 x3 a cin b a 3⌧ 2⌧ VA cout s z7 b cin VA cout z6 a b cin a VA cout s z5 z4 b HA s cout z3 s z2 z1 b ⌧ z0 HA s 0 3.7 Kombinatorischer Multiplizierer 139 Zur Mitschrift: x3 + + + = x3 x2 z7 x1 x2 x1 x0 x 3 · y3 z6 x2 · y 3 x3 · y 2 z5 x1 · y3 x2 · y2 x3 · y1 z4 x0 y3 · y · y3 x 0 · y3 x 1 · y2 x 2 · y1 x 3 · y0 z3 y2 y2 x0 · y 2 x1 · y 1 x2 · y 0 y1 x0 · y1 x1 · y0 y0 x 0 · y0 z2 z1 z0 y1 3 y0 2 1 x0 y 3 2 1 0 x1 ⌧ a b a HA cout 3 b cin a VA ⌧ cout s y 2 b VA cout s 1 cin a 2⌧ s cout 0 x2 a cin b a 3 cin a cout s 2 cin VA cout s y 1 b 3⌧ VA 2⌧ VA ⌧ cout b a b HA cout s s 0 x3 a cin b a 3⌧ 2⌧ VA cout s z7 b cin VA cout z6 a b cin a VA cout s z5 z4 b HA s cout z3 s z2 z1 b ⌧ z0 HA s 0 140 3 Arithmetische Schaltungen b) Tragen Sie in die Multiplizierer-Schaltung den längsten Pfad ein. Wie lange (in Gatterlaufzeiten ⌧ ) dauert die Ausführung? 16⌧ Der Hardwareaufwand der gezeigten Schaltung ist sehr hoch: Mit steigender Wortbreite n steigt der notwendige Hardwareaufwand mit ca. n2 . 3.8 Sequentieller Multiplizierer 141 3.8 Sequentieller Multiplizierer Mit einer sequentiellen Schaltung kann der Hardwareaufwand reduziert werden. Die nächste Abbildung skizziert eine sequentielle Schaltung, die zur Multiplikation vorzeichenloser Zahlen der Wortbreite n = 4 verwendet werden kann. MR y3 y2 y1 y0 Add PR 0 0 0 0 PR0 0 x3 x2 x1 x0 Das Multiplikand-Register MR ist n = 4 Bit breit, das Produkt-Register PR ist 2n + 1 = 9 Bit breit. PR0 ist das niederwertigste Bit des im Produktregister gespeicherten Werts. Der sequentielle Ablauf ist wie folgt: • Zunächst wird der Multiplikand im Multiplikand-Register MR und der Multiplikator in den unteren n Bits des Produkt-Registers abgelegt. Die restlichen Bits des Produktregisters werden mit 0 initialisiert. • Anschließend wird iterativ n = 4 mal folgendes ausgeführt: • Wenn PR0 = 1, dann • wird der in MR stehende Wert zu den Bits PR7 ... PR4 des Produktsregisters addiert; ein ggf. auftretender Überlauf wird in PR8 abgelegt; anschließend • wird das gesamte Produktregister um eine Stelle nach rechts geschoben; dabei wird von links mit Nullen aufgefüllt. • Wenn PR0 = 0, dann • wird keine Addition durchgeführt, sondern lediglich das gesamte Produktregister um eine Stelle nach rechts geschoben; dabei wird wieder von links mit Nullen aufgefüllt. • Nach n = 4 Iterationen (=Runden) steht im Produktregister das Ergebnis. 142 a) 3 Arithmetische Schaltungen Tragen Sie in folgende Abbildung für n = 4 die Registerinhalte ein, die sich für die Multiplikation 13 · 5 = 65 ergeben. 0 1 0 1 Add 0 0 0 0 0 1 1 0 1 Initialisierung Nach Addition: 0 0 1 0 1 1 1 0 1 Erste Runde Nach Schieben: 0 0 0 1 0 1 1 1 0 Erste Runde Zweite Runde Nach Addition: Nach Schieben: 0 0 0 0 1 0 1 1 1 Zweite Runde Nach Addition: 0 0 1 1 0 0 1 1 1 Dritte Runde Nach Schieben: 0 0 0 1 1 0 0 1 1 Dritte Runde Nach Addition: 0 1 0 0 0 0 0 1 1 Vierte Runde Nach Schieben: 0 0 1 0 0 0 0 0 1 Vierte Runde 3.8 Sequentieller Multiplizierer 143 Nachfolgende Abbildung zeigt den (unvollständigen) Aufbau einer Schaltung zur Implementierung des gezeigten Multiplikationsverfahrens. b) Vervollständigen Sie die Schaltung so, dass sie vorzeichenlose Binärzahlen multipliziert. Steuerung 1 0 n Multiplikator n n 3.7 Multiplizierer 141 n Init/>>1 0 n Sequentielle Schaltung zur 0..n-1 Multiplikation vorzeichenloser Zahlen 0..n-1 PR Mit einer sequentiellen Schaltung kann der Hardwareaufwand deutlich reduziert werden. 2n 1 Die nächste Abbildung skizziert eine sequentielle Schaltung, die zur Multiplikation von n..2n n..2n-1 vorzeichenloser Zahlen der Wortbreite n = 4 verwendet werden kann: MR 0 n+1 Produkt y3 y2 y1 y0 1 2n Add n+1 0 PR0 n PR 0 0 0 0 0 x3 x2 x1 x0 Addierer MR Multiplikand n n Das Multiplikand-Register MR ist n = 4 Bit breit, das Produkt-Register PR ist 2n + 1 = 9 Bit breit. PR0 ist das niederwertigste Bit des im Produktregister gespeicherten Werts. DernAblauf ist wie folgt: • Zunächst wird der Multiplikand im Multiplikand-Register MR und der Multiplikator in den unteren n Bits des Produkt-Registers abgelegt. Die restlichen Bits des Produktregisters werden mit 0 initialisiert. • Anschließend wird iterativ n = 4 mal folgendes ausgeführt: • Wenn PR0 = 1, dann • wird der in MR stehende Wert zu den Bits PR7 ... PR4 des Produktsregisters addiert; ein ggf. auftretender Überlauf wird in PR8 abgelegt; anschließend • wird das gesamte Produktregister um eine Stelle nach rechts geschoben; dabei wird von links mit Nullen aufgefüllt. • Wenn PR0 = 0, dann • wird keine Addition durchgeführt, sondern lediglich das gesamte Produktregister um eine Stelle nach rechts geschoben; dabei wird wieder von links mit Nullen aufgefüllt. • Nach n = 4 Iterationen (=Runden) steht im Produktregister das Ergebnis.