www.matheportal.wordpress.com Übungsaufgabe für das

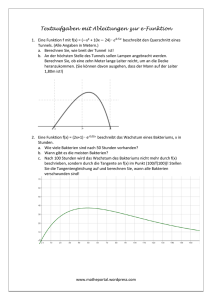
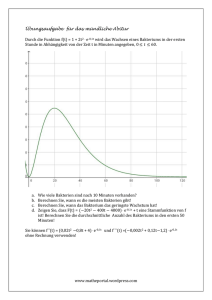
Übungsaufgabe für das mündliche Abitur
Durch die Funktion f(t) = 1 + 2t2 . e-0,1t wird das Wachsen eines Bakteriums in
Abhängigkeit von der Zeit t in Minuten angegeben.
a.
b.
c.
d.
Wie viele Bakterien sind nach 10 Minuten vorhanden?
Berechnen Sie, wann es die meisten Bakterien gibt!
Berechnen Sie, wann das Bakterium das geringste Wachstum hat!
Zeigen Sie, dass F(x) = -20 . (t2 + 20t+200) . e-0,1t + t eine Stammfunktion von f ist!
Berechnen Sie die durchschnittliche Anzahl des Bakteriums in den ersten 50
Minuten!
Sie können f´´(t) = (0,02t2 -0,8t +4) . e-0,1t und f´´´(t) =(-0,002t2 + 0,12t-1,2) . e-0,1t ohne
Rechnung verwenden!
www.matheportal.wordpress.com
Lösung:
a. f(10) = 74,57, d.h. 74 Bakterien.
b. f´(x) = 4t e-0,1t + 2t2 (-0,1) e-0,1t = e-0,1t (4t-0,1t2)
f´(t) =0
t= 0 v t = 20
f´´(t) = (-0,02t2 -0,8t +4) . e-0,1t
f``(0) =4
f``(20 ) = -2,7<0 -> Maximum
Ränder: x = 0 ist ein Minimum; lim f (x)  0 , d.h. wir haben das absolute
x
Maximum
Nach 20 Minuten gibt es die meisten Bakterien!

c. f´´(x) = 0  0,02t2 -0,8t +4= 0  t = 5,85 v t = 34,14
f´´´(5,85) = -0,31<0 maximale Steigung
f`´´´(34,14) = 0,01 >0 -> minimale Steigung
Nach 34,14 Minuten ist das Wachstum am geringsten.
d. F(x) = (-20t2 – 400t -4000) e-0,1t +t
F´(x) = (-40t-400) e-0,1t + (-20t2 – 400t -4000) e-0,1t (-0,1)+1 = e-0,1t (-40t-400+2t2
+40t +400) +1=1 + 2t2 . e-0,1t
1 50
1
1
1
50
f (x)dx  F(x)0  (F(50)  F(0))  (440,60  (4000))  71,188

50 0
50
50
50
Es sind durchschnittlich 71 Bakterien vorhanden.

www.matheportal.wordpress.com