Neuronale Netze, Fuzzy Control, Genetische Algorithmen Prof
Werbung
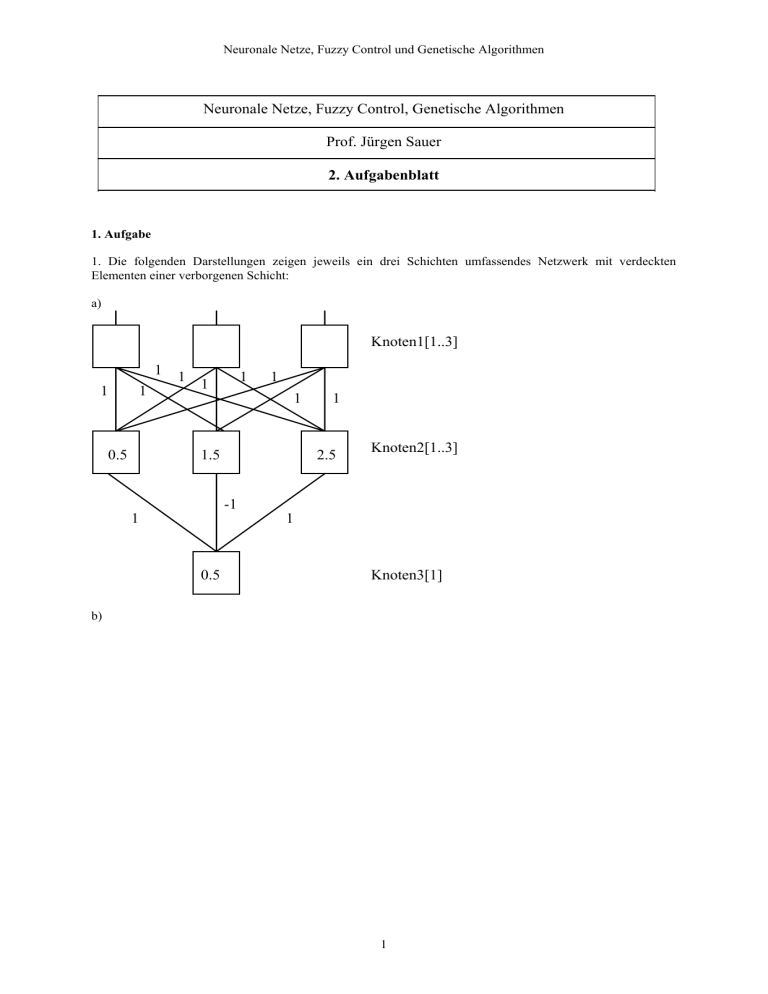
Neuronale Netze, Fuzzy Control und Genetische Algorithmen Neuronale Netze, Fuzzy Control, Genetische Algorithmen Prof. Jürgen Sauer 2. Aufgabenblatt 1. Aufgabe 1. Die folgenden Darstellungen zeigen jeweils ein drei Schichten umfassendes Netzwerk mit verdeckten Elementen einer verborgenen Schicht: a) Knoten1[1..3] 1 1 1 0.5 1 1 1 1 1 1.5 1 2.5 Knoten2[1..3] -1 1 1 0.5 Knoten3[1] b) 1 Knoten1[1..3] 1 1 1 1 1 1 Knoten2[1..2] 1.5 1.5 1 1 1 -1 -1 Knoten3[1] 0.5 Die in den Elementen (Knoten des Netzwerks) angegebenen Zahlen sind Schwellenwerte für die Aktivierungsfunktion. Die Zahlen an den Kanten (Verbindungen) sind die den Synapsen zugeordneten Gewichtswerte. Die Aktivierungsfunktion der Ausgabeschicht und der mittleren Schicht ist die "Schwellwert"Funktion (Sprung-), die Aktivierungsfunktion der Eingabeschicht ist linear. Zeige (durch Berechnung, die einzelnen Rechenschritte sollen nachvollziehbar protokolliert werden), daß diese Netzwerke die folgende Boolesche Funktion (Parity-Bit) lösen. Eingabe 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1 Ausgabe 0 1 1 0 1 0 0 1 0 1 0 1 0 1 0 1 Welche Aktivierungen nehmen die einzelnen Knoten der unter a) bzw. b) vorgegebenen Netzwerke an? a) Knoten1[ 1 0 0 0 0 1 1 1 1 2 0 0 1 1 0 0 1 1 3] 0 1 0 1 0 1 0 1 Knoten2[1 2 3] 2 Knoten3[ 1 ] b) Knoten1[ 1 0 0 0 0 1 1 1 1 2 0 0 1 1 0 0 1 1 3] 0 1 0 1 0 1 0 1 Knoten2[ 1 2] Knoten3[ 1 ] 2. Aufgabe 1. Mit welchem einstufigen Netz, das aus einer Ein- und Ausgabeschicht besteht, kann die folgende binäre Funktion Eingabe 0 0 0 1 1 0 1 1 Ausgabe 0 1 0 0 bearbeitet werden? Das Netz soll so einfach wie möglich gestaltet werden. _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ 2. Gib die Aktivierungsfunktion an, die für die Bildung der Elemente der Ein- und Ausgabeschicht verwendet werden soll? Aktivierungsfunktion der Elemente der Eingabeschicht _________________________________________ Aktivierungsfunktion der Elemente der Ausgabeschicht ________________________________________ 3. Führe die einzelnen Lernschritte zum Trainieren des unter 1. angegebenen Netzes nach der Deltaregel aus, so daß die unter 1. angegebene binäre Funktion korrekt abgebildet wird. Alle erforderlichen Rechenschritte sind anzugeben (insbesondere zur Ermittlung der Gewichte). Die Gewichte sind zu Beginn mit 0 initialisiert, die Lernrate hat den Wert 0.25. Die ermittelten Zahlen sind in die folgende Tabelle einzutragen. a) Gib den ersten Lernschritt an? 3 Eingabe Ziel Ausgabe Fehler Δwij wij b) Wurde im ersten Lernschritt das vorgegebene Ziel erreicht? __________________ c) Falls das Ziel nicht erreicht wurde, gib ein Maß für die Höhe des Fehlers an. __________________________ d) Führe den nächsten Lernschritt aus. Eingabe Ziel Ausgabe Fehler Δwij wij Δwij wij e) Wie hoch ist jetzt der Fehler? Die Berechnung soll nach der unter c) angegebenen Formel erfolgen. f) Falls noch ein Lernschritt erforderlich ist, führe diesen 3. Lernschritt aus. Eingabe Ziel Ausgabe Fehler Wurde jetzt das Lernziel erreicht? ______________________________________________________________ Begründe die zuletzt gemachte Angabe! _________________________________________________________ 4. Zeige, daß die unter 1. Angegebene binäre Funktion das Kriterium der „linearen Tremmbarkeit“ erfüllt. ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ ______________________________________________________________________________________ 5. Berechne zu dem unter 1 definierten Netz die zugeordneten Gewichte. a) Stelle die zur Berechnung notwendigen Gleichungen bzw. Ungleichnugen auf, die aus dem Prinzip der linearen Trennbarkeit resultiern. _____________________________________________________________________________________ _____________________________________________________________________________________ 4 _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ b) Leite aus dem unter a) angegebenen Ungleichungen eine Lösung für die Gewichte ab. _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ 5