Übungen zur Vorlesung Maschinelles Lernen WS 2005/06 Blatt 4

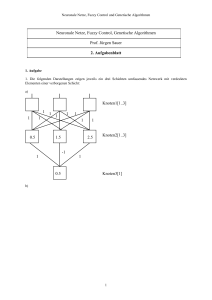
Prof. Dr. Hans Kleine Büning
Oliver Kramer
Paderborn, den 25. November 2005
Übungen zur Vorlesung
Maschinelles Lernen
WS 2005/06
Blatt 4
AUFGABE 1 :
Resiliant Backpropagation (Rprop).
Als Lernregel für die Gewichte eines mehrschichtigen Perzeptrons schlugen Riedmiller und Braun
1993 folgende als Rprop bekannte Regel vor:

∂E

 −∆ij (t) , falls ∂wij (t) > 0
∂E
∆wij (t) =
(t) < 0
+∆ij (t) , falls ∂w
ij


0 , sonst
Der Änderungswert ∆ij wird zusätzlich durch folgende Regel spezifiziert:

∂E
∂E
+

 η · ∆ij (t − 1) , falls ∂wij (t − 1) · ∂wij (t) > 0
∂E
∂E
∆ij (t) =
η − · ∆ij (t − 1) , falls ∂w
(t − 1) · ∂w
(t) < 0
ij
ij


∆ij (t − 1) , sonst
mit η − = 0.5, η + = 1.2. Der Anfangswert der Änderungen ∆ij (0) ist für alle Gewichte gleich und
wird duch den Parameter ∆0 des Rprop-Verfahrens bestimmt. Beschreiben Sie, auf welche Weise
die Gewichtsanpassung erreicht wird. Welche Vorteile könnte diese Art der Gewichtsanpassung
gegenüber der Ihnen bekannten δ- bzw. Backpropagation-Regel haben?
AUFGABE 2 :
Self-organizing feature maps
a) Nennen Sie die Komponenten des SOM (self organizing feature map)-Algorithmus von Kohonen
und beschreiben Sie den Ablauf des Lernverfahrens.
b) Wir befinden uns im Datenraum D ∈ IR3 . Gegeben seien folgende Eingabedaten:
 
 
 
0
0
1
x1 =  0  x2 =  1  x3 =  0 
1
0
0
Dieser Datenraum D soll in einen Kartenraum K einer SOM mittels des Kohonen-Algorithmus
abgebildet werden. Die Ausgabeschicht der SOM bestehe aus drei Neuronen ni , 1 ≤ i ≤ 3, die
linear angeordnet sind. Die Neuronen nx und ny haben den Abstand |x − y| mit 1 ≤ x, y ≤ 3
voneinander. Als Nachbarschaftsfunktion wird
exp(
−|di,i∗ |2
)
2σ 2
1
verwendet, wobei di,i∗ den Abstand zwischen Neuron i und dem Gewinnerneuron i∗ angibt. Die
Gewichtsvektoren wi , 1 ≤ i ≤ 3 werden mit folgenden Werten initialisiert:
 
 
 
2
3
1
w1 =  2  w2 =  1  w3 =  3 
1
2
3
Wenden Sie den SOM-Lernalgorithmus auf den oben genannten Datensatz an und simulieren Sie
die Durchführung einer Iteration. Benutzen Sie für die Lernrate η = 0.5 und als konstanten Nachbarschaftsradius σ = 0.9.
2