G Zahlendarstellung und Rechnerarithmetik

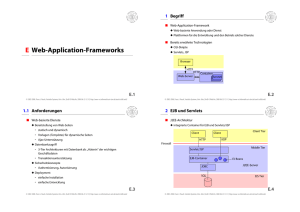
1 Einordnung
G Zahlendarstellung und
Rechnerarithmetik
Ebene 6
Problemorientierte Sprache
Ebene 5
Assemblersprache
Ebene 4
Betriebssystem
Ebene 3
ISA (Instruction Set Architecture)
Ebene 2
Mikroarchitektur
Ebene 1
Digitale Logik
Ebene 0
Physik
G.1
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
2 Zahlendarstellung
2.1 Positive ganze Zahlen (2)
2.1 Positive ganze Zahlen
■ Dualsystem, Binärsystem
◆ Beispiel:
■ Positionale Zahlendarstellung
3
2
1
1011 2 = ( 1, 0, 1, 1 ) 2 = 1 ⋅ 2 + 0 ⋅ 2 + 1 ⋅ 2 + 1 ⋅ 2
◆ Ziffern
◆ Position der Ziffern gewichtet ihren Wert
0
◆ Allgemein: n-stellige Dualzahl
( z n – 1, z n – 2, …, z 2, z 1, z 0 ) 2
= z n – 1 ⋅ 2 n – 1 + z n – 2 ⋅ 2 n – 2 + …+ z 2 ⋅ 2 2 + z 1 ⋅ 2 1 + z 0 ⋅ 2 0
■ Dezimalsystem
◆ Beispiel:
G.2
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3
2
1
4711 = ( 4, 7, 1, 1 )10 = 4 ⋅ 10 + 7 ⋅ 10 + 1 ⋅ 10 + 1 ⋅ 10
0
mit z i ∈ {0, 1 }
◆ Allgemein: n-stellige Dezimalzahl
( z n – 1, z n – 2, …, z 2, z 1, z 0 ) 10
= z n – 1 ⋅ 10n – 1 + z n – 2 ⋅ 10 n – 2 + …+ z 2 ⋅ 10 2 + z 1 ⋅ 101 + z 0 ⋅ 10 0
mit z i ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
G.3
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.4
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
2.1 Positive ganze Zahlen (3)
2.2 Konvertierung der Darstellung
■ Allgemein
■ Umwandlung von einer Zahlendarstellung in die andere
◆ Darstellung natürlicher Zahlen durch Zahlensystem zu einer beliebigen Basis
b≥1
( z n – 1, z n – 2, …, z 2, z 1, z 0 ) b
= z n – 1 ⋅ b n – 1 + z n – 2 ⋅ b n – 2 + …+ z 2 ⋅ b 2 + z 1 ⋅ b 1 + z 0 ⋅ b 0
◆ Basis des Ziel-Zahlensystems als Divisor
◆ Reste bilden die Ziffern der Darstellung
◆ Beispiel: 1910 → x 2
mit z i ∈ {0, 1, …, b – 1 }
■ Typische Basen für Rechnerarithmetik
◆ b = 2 Dualsystem
◆ b = 8 Oktalsystem z i ∈ {0, 1, 2, 3, 4, 5, 6, 7 }
19 ÷ 2 = 9
9÷2 = 4
Rest 1
Rest 1
4÷2 = 2
2÷2 = 1
Rest 0
Rest 0
1÷2 = 0
Rest 1
least significant digit
most significant digit
◆ b = 10 Dezimalsystem
x = ( 1, 0, 0, 1, 1 ) 2
◆ b = 16 Hexadezimalsystem
z i ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F }
G.5
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.6
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
2.2 Konvertierung der Darstellung (2)
2.3 Darstellung positiver Zahlen im Rechner
■ Alternative
■ Zahlenspeicherung in Registern
◆ Finden der Stufenzahlen und deren Vielfache
◆ einzelne Flip-Flops speichern eine Ziffer (Bit)
◆ Beispiel: 1910 → x 8
◆ mehrere Flip-Flops speichern eine Zahl
• Stufenzahlen des Oktalsystems: 1, 8, 64, 512 ...
■ Registerbreite
• Welche Stufenzahl passt gerade noch hinein: 8
• Wie oft passt sie hinein:
19 ÷ 8 = 2
Rest 3
= 1 Byte
◆ Wort
= 16 Bit / 32 Bit (Word)
◆ Doppelwort = 32 Bit / 64 Bit (Double Word)
• Wiederholung mit Rest und nächst kleinerer Stufenzahl:
3÷1 = 3
◆ 8 Bit
◆ Vierfachwort = 64 Bit / 128 Bit (Quad Word)
Rest 0
• Wiederholung bis Stufenzahl 1 erreicht wurde
■ Wortbreite hängt von Prozessorarchitektur ab
• Ergebnis der Divisionen bilden die Ziffern: x = 238
G.7
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.8
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3 Binäre Addition
3.1 Halbaddierer
■ Schriftliche Addition
■ Addition in erster (rechter) Spalte
◆ Verfahren wie beim Dezimalsystem
10011
+1001
11
11100
Übertrag
◆ zwei Eingänge: erste Ziffer von jeder Zahl
Kontrolle:
◆ zwei Ausgänge: erste Ziffer des Ergebnisses, Carry
19 + 9 = 28
◆ Wahrheitstabelle:
a
0
0
1
1
◆ Übertrag wird auch Carry genannt
■ Feste Registerbreite und Addition, z.B. vier Bit
1011
+1001
1 11
0100
Kontrolle:
Übertrag
b
0
1
0
1
s
0
1
1
0
Blockschaltbild:
c
0
0
0
1
a
b
c
HA
s
◆ Schaltung:
11 + 9 = 20 = 16 + 4
c
a
◆ letzter Übertrag gehört zum Ergebnis
b
◆ kann aber nicht mehr dargestellt werden
+
c = a⋅ b
s = a⋅ b+ a⋅ b = a⊕ b
s
G.9
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3.2 Volladdierer
G.10
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3.2 Volladdierer
■ Addition in anderen Spalten
■ Schaltung
◆ drei Eingänge: je eine Ziffer der Summanden und Carry von vorheriger Ziffer
◆ zwei Ausgänge: Summenziffer und Carry
◆ Aufbau mit Halbaddierern
c
a
◆ Wahrheitstabelle:
a
b
cin
s
cout
b
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
0
1
0
0
0
1
0
1
1
1
cin
HA
s
c
cout
s
s
HA
◆ realer Aufbau als zweistufiges Schaltnetz (geringere Gatterlaufzeiten)
■ Blockschaltbild
a
b
cin
G.11
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
cout
FA
s
G.12
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3.3 Paralleles Addierwerk
3.4 Serielles Addierwerk
■ Schaltnetz zur Addition n-Bit langer Summanden
an-1 bn-1
a2 b2
a 1 b1
■ Synchrones Schaltwerk zur Addition n-Bit langer Summanden
a0 b0
Clk
cin
FA
FA
...
c
FA
c
an-1
bn-1
FA
c
a1 a0
FA
b1 b0
c
s
sn-1
c
D
s1 s0
cout
Q
cout
sn-1
s2
s1
s0
◆ Schieberegister für Summanden und Ergebnis
◆ je eine Stelle pro Takt wird addiert (Ergebnis nach n Takten)
◆ lange Gatterlaufzeit bis Endergebnis stabil
◆ Carry-Flip-Flop muss initialisiert werden
• Gatterlaufzeit: t = 2n ⋅ Δt
◆ Ripple Carry Adder (RCA)
G.13
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3.5 Carry-Look-Ahead-Addierer
G.14
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3.5 Carry-Look-Ahead-Addierer (2)
■ Beschleunigung der Addition
■ Berechnung der Überträge mit maximal 2 Gatterlaufzeiten möglich
◆ Vermeidung des sequentiellen Durchlaufs der Überträge
◆ max. Anzahl der Gattereingänge hängt von der Breite des Addierers ab
◆ Idee: parallele Berechnung aller Stellenüberträge für jede Stelle i
a0
a1
a2
a3
■ Es gilt für Stelle i
◆ ci + 1 = a i ⋅ bi + ( a i + b i ) ⋅ c i = G i + Pi ⋅ c i mit
b0
b1
b2
b3
G i = a i ⋅ b i gibt an, ob Stelle i Carry generiert (Generate)
P i = ai + b i gibt an, ob Stelle i Carry weitergeben muss (Propagate),
c0
falls vorherige Stelle Carry generiert oder weitergibt
carry
logic
◆ Schaltfunktionen für Überträge
c1 = G 0 + P 0 ⋅ c 0
c2 = G 1 + P 1 ⋅ c 1 = G 1 + P 1 ⋅ G 0 + P 1 ⋅ P 0 ⋅ c 0
c3 = G 2 + P 2 ⋅ G 1 + P 2 ⋅ P 1 ⋅ c1 = G 2 + P 2 ⋅ G 1 + P 2 ⋅ P 1 ⋅ G 0 + P 2 ⋅ P 1 ⋅ P 0 ⋅ c0
...
c4
carry
logic
FA
c s
c3
s3
carry
logic
FA
c s
c2
carry
logic
FA
c s
s2
c1
s1
FA
c s
s0
◆ Kaskadierung möglich
G.15
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
• pro CLA-Addierer nur 4Δt Verzögerung
G.16
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
3.6 Carry-Select-Addierer
3.7 Carry-Save-Addierer
■ Beschleunigung der Addition
■ Mehr als zwei Summanden
◆ Idee: nicht auf das Carry des niederwertigen Blocks warten, sondern beide
Ergebnisse berechnen und später selektieren
a3 a2 a1 a0 b3 b2 b1 b0
a3 a2 a1 a0 b3 b2 b1 b0
4-Bit RCA Addierer
4-Bit RCA Addierer
c
1
c
◆ Überträge aus ersten Addition werden in der nächsten Addition berücksichtigt
(keine Weitergabe der Überträge in der laufenden Addition)
■ Beispiel: 4-Bit CSA für vier Summanden
a3 b3 c3
0
c
FA
s
d3
c3
a2 b2 c2
c
FA
s
d2
c0
c
FA
s
a1 b1 c1
c
FA
a0 b0 c0
s
c
d1
c
FA
s
FA
s
d0
c
FA
HA
c s
s
s3 s2 s1 s0
Standardaddierer
◆ Multiplexer selektiert Endergebnis
G.17
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4 Binäre Subtraktion
G.18
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4.2 Einerkomplement-Darstellung
■ Subtrahierer kann ähnlich wie Addierer entwickelt werden
■ Berechnung des Einerkomplements einer Zahl N bei n Ziffern
◆ C = 2 n – N – 1 bei n Ziffern/Bits
✱ Verwendung von Addierern zur Subtraktion
◆ Komplement C entspricht dem Wert –N
◆ Idee: a – b = a + ( – b )
■ Darstellung positiver ganzer Zahlen
4.1 Darstellung negativer ganzer Zahlen
◆ höherwertigste Ziffer z n – 1 = 0
◆ andere Ziffern unbeschränkt
■ Vorzeichen und Betrag
◆ Wert: ( z n – 1 , …, z 1, z 0 ) 2 =
◆ ein Bit repräsentiert Vorzeichen
∑zi ⋅
2
i
i
◆ andere Bits repräsentieren Betrag der Zahl
■ Darstellung negativer ganzer Zahlen
◆ Beispiel:
◆ höherwertigste Ziffer z n – 1 = 1
01001 2 = 9
◆ andere Ziffern unbeschränkt
11001 2 = – 9
◆ Wert: ( z n – 1 , …, z 1, z 0 ) b = – 2 n + 1 + ∑z i⋅ 2
▲ Nachteil: Vorzeichen muss für Berechnungen ausgewertet werden
i
i
G.19
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.20
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4.2 Einerkomplement-Darstellung (2)
4.2 Einerkomplement-Darstellung (3)
■ Beispiel: Darstellungslänge n=4
◆ 10002 = –
24
■ Addition
+ 1 + 8 = –7
kleinste negative Zahl
◆ 11112 = – 2 4 + 1 + 15 = 0
größte (negative) Zahl
◆ Einsatz von leicht modifizierten Standardaddierern für Zahlen in
Einerkomplement-Darstellung
◆ Carry-out muss zum Ergebnis addiert werden
• ohne Überlauf kommt Carry-out nur bei Addition von ein oder zwei
negativen Zahlen vor
▲ Nachteil
◆ Null hat zwei unterschiedliche Darstellungen (0000 und 1111 bei Länge 4)
• X + ( – Y ) mit – Y als 2 n – Y – 1 wird zu X + 2 n – Y – 1
Übertrag 2 n gleicht –1 aus
✱ Vorteil der Einerkomplement-Darstellung
• ( –X ) + ( –Y ) wird zu 2 n – X – 1 + 2 n – Y – 1
Übertrag 2 n gleicht –1 aus, übrig bleibt 2 n – ( X + Y ) – 1 also eine Zahl im
Einerkomplement
◆ einfache Umwandlung von positiver zu negativer Zahl und umgekehrt
• jede Ziffer wird „invertiert“: z i' = 2 – 1 – z i
• Beispiel: aus 1000 2 wird 01112 (aus –7 wird 7)
■ Subtraktion
◆ vorherige Komplementbildung durch Invertierung der Ziffern
G.21
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4.2 Einerkomplement-Darstellung (4)
4.2 Einerkomplement-Darstellung (5)
■ Additionsschaltwerk für Einerkomplement
an-1 bn-1
a2 b2
G.22
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
■ Einerkomplement heute kaum mehr im Einsatz
a 1 b1
a0
◆ doppelte Darstellung der Null
b0
◆ Verwendung modifizierter Standardaddierer
FA
FA
...
c
FA
c
• je ein Schaltnetz für rein positive Zahlen und Zahlen im Einerkomplement
erforderlich (oder ein umschaltbares Schaltnetz)
HA
c
c
cout
HA
...
c
HA
HA
c
sn-1
HA
c
s2
c
s1
s0
◆ Rückführen und Addieren des Carry-out-Signals
G.23
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.24
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4.3 Zweierkomplement-Darstellung
4.3 Zweierkomplement-Darstellung (2)
■ Berechnung des Zweierkomplements einer Zahl N bei n Ziffern
◆C =
■ Beispiel: Darstellungslänge n=4
– N bei n Ziffern/Bits
◆ 1000 2 = – 2 4 + 8 = – 8
kleinste negative Zahl
◆ Komplement C entspricht dem Wert –N
◆ 1111 2 = – 2 4 + 15 = –1
größte negative Zahl
2n
■ Darstellung positiver ganzer Zahlen
✱ Vorteil der Zweierkomplement-Darstellung
◆ höherwertigste Ziffer z n – 1 = 0
◆ eindeutige Darstellung der Null (0000 bei Länge n=4)
◆ andere Ziffern unbeschränkt
◆ Wert: ( z n – 1, …, z 1, z 0 )2 =
∑zi ⋅
2
◆ einfache Umwandlung von positiver zu negativer Zahl und umgekehrt
i
• jede Ziffer wird „invertiert“: z i' = 2 – 1 – z i
i
• anschließend 1 auf niederwertigste Stelle addieren
(Zweierkomplement ist um eins größer als Einerkomplement)
■ Darstellung negativer ganzer Zahlen
◆ höherwertigste Ziffer z n – 1 = 1
• Beispiel: aus 1001 2 wird 0110 2 und dann 01112 (aus –7 wird 7)
◆ andere Ziffern unbeschränkt
◆ Wert: ( z n – 1, …, z 1, z 0 )2 = – 2 n + ∑z i ⋅ 2
i
i
G.25
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4.3 Zweierkomplement-Darstellung (3)
G.26
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4.4 Subtraktion im Zweierkomplement
▲ Nachteil
■ Addier- und Subtrahierwerk
◆ für kleinste negative Zahl ist das Zweierkomplement nicht mehr darstellbar
a3 b3
a2 b2
a1 b1
a0 b0
• ( 1000 ) 2 = –8 wird zu ( 1000 ) 2 = 8 (?)
◆ Einsatz von Standardaddierern für Zahlen im Zweierkomplement
Standardaddierer
s3
✱ Subtraktion
+
cout
+
✱ Addition
+
+
• 8 bereits außerhalb des Darstellungsbereichs (Überlauf)
s2
s1
cin
ADD, SUB
s0
◆ beim Subtrahieren:
◆ vorherige Komplementbildung eines Summanden erfordert
• Invertieren der b-Eingänge durch XOR-Gatter
• Invertierung der Ziffern
• Addieren von 1 durch gesetztes Carry-in
• Addition von 1
kann durch gesetzten Carry-Eingang erzielt werden
◆ Überlauferkennung: c out ≠ cin
• bei Subtraktion ist gesetztes Carry-out der Normalfall
G.27
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.28
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
4.5 Zahlenraum der ZweierkomplementDarstellung
5 Binäre Multiplikation
■ Schriftliche Multiplikation auf Binärzahlen (rein positive Zahlen)
■ Zahlenraum für n-stellige Register
0011 x 1010
◆ Beispiel: n=4
1111
15
1110
14 –1
–2
1101
13 –3
0000
0
0
0001
1
0010
1
2
2
0011
3
3
1100 12 –4
1011
positiver Wert
Wert im Zweierkomplement
5
–7
9
1001
6
7
–8
◆ Realisierung in Hardware: Addierer und Schieberegister
1000
◆ Realisierung in Software: Addition und Bittest/Schieberegister
• einige Prozessoren besitzen keine Multiplikationshardware
0101
6
7
8
5
Kontrolle: 3 x 10 = 30
111102 = 30
1
0
1
0
■ Übertragung auf den Rechner
4 4 0100
–5
11
–6
10
1010
Binärdarstellung
0011
0000
0011
+
0000
00011110
0110
0111
G.29
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.1 Vorzeichenlose Multiplikation
5.1 Vorzeichenlose Multiplikation (2)
■ Alternative A: serielles Schaltwerk zur Multiplikation
an-1
n
cout
...
a1
n
a0
n-Bit-Addierer
n
bn-1
...
b1
■ Alternative B: Array-Multiplizierer
◆ Schaltwerk für das schriftliche Multiplikationsschema
b0
◆ Beispiel: n = 4
shift right b
add
p2n-1 ... pn+1 pn pn-1 ...
a3
Steuerwerk
shift right p
clear p
p1
G.30
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
p0
a2
a3b3
+
◆ Lösche p (clear p)
p7
◆ n-mal:
• ermittle b0 (shift right b)
a1
p6
a0
x
a3b1
a3b2 a2b2
a2b3 a1b3
p5
p4
b3
b2
b1
b0
UND-Verknüfung
a3b0 a2b0 a1b0 a0b0
a2b1 a1b1 a0b1
0
a1b2 a0b2
0
0
a0b3
0
0
0
p3
p2
p1
p0
◆ Einsatz von Carry-Save-Addierern für die einzelnen Zeilen
• addiere a auf (p2n-1,...pn+1, pn)2 oder nicht je nach b0 (add)
• verschiebe p einschließlich cout der vorherigen Addition (shift right p)
G.31
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.32
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.1 Vorzeichenlose Multiplikation (3)
5.1 Vorzeichenlose Multiplikation (4)
■ Alternative B: Array-Multiplizierer
■ Alternative C: Alternative B und Wallace-Baum von CS-Addierern
◆ Schaltwerk für n = 4
sin
ai
◆ baumförmige statt sequentielle Anordnung der CSA
a3
a2
a1
a0
◆ Beispiel: n = 8
z3 z 2 z1
bi
bi
cout
cin
FA
ai
b0
b1
sout
z4
z5
z6
b2
b3
z7
z8
z8 z7 z6 z5 z4 z 3 z2 z 1
CSA
CSA
CSA
CSA
CSA
p6
p5
p4
p3
p2
p1
p0
CSA
CSA
Wallace-Baum
CSA
CSA
CSA
RCA
CSA
p7
CSA
Vorteil: geringere Gatterlaufzeit
RCA
CSA-Kette
G.33
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.1 Vorzeichenlose Multiplikation (5)
G.34
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.2 Multiplikation für ZweierkomplementDarstellung
■ Alternative D: zweistufiges Schaltnetz für Multiplizierer
■ n-Bit-breites Ergebnis bei Multiplikation n-Bit breiter Zahlen auch für
Zweierkomplement korrekt
◆ z.B. als PROM/ROM
✱ Schnellste Variante
◆ Beispiel: –2 x 3 = –6 (bein n = 4)
▲ Extrem aufwändig
1110 x 0011
◆ 2 2n ⋅ 2n Bits notwendig
0000
0000
1110
+
1110
00101010
■ Übergang zu kleineren Blockmultiplizierer (Radixmultiplizierer)
◆ Blockmultiplizierer für k-Bit als ROM-Implementierung
◆ blockweises Multipliziereren
◆ Addieren der Blöcke mit CSA
0
0
1
1
10102 = –6
▲ Problem: Überlauf — Ergebnis passt meist nicht in n Bits
◆ 2n-Bit-breites Ergebnis ist nicht korrekt
001010102 = 42
G.35
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.36
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.2 Multiplikation für Zweierkomplement (2)
5.2 Multiplikation für Zweierkomplement (3)
■ Alternative A: Erweiterung der Faktoren auf 2n-Bit
■ Alternative B: Addition eines Korrektursummanden
◆ Vorzeichenerweiterung
◆ a ⋅ ( –b) = a ⋅ ( 2n – b) = 2n ⋅ a – ( a ⋅ b )
◆ ( –a ) ⋅ b = ( 2n – a ) ⋅ b = 2n ⋅ b – ( a ⋅ b )
• z.B. aus 1110 wird 11111110, aus 0011 wird 00000011
◆ ( – a ) ⋅ ( –b ) = ( 2 n – b ) ⋅ ( 2 n – a ) = 2 2n – 2 n ⋅ a – 2 n ⋅ b + a ⋅ b
▲ Nachteil
statt 2 2n – a ⋅ b bzw. a ⋅ b
◆ 2n-Bit-breiter Addierer
◆ 2n statt n Runden/Additionen (bei seriellem Addierer)
◆ Korrektursummand für a ⋅ ( – b ) :
2 2n – 2 n ⋅ a = 2 n ⋅ ( 2 n – a )
◆ Korrektursummand für ( – a ) ⋅ b :
2 2n – 2 n ⋅ b = 2 n ⋅ ( 2 n – b )
◆ Korrektursummand für ( – a ) ⋅ ( –b ) :
2n ⋅ a + 2n ⋅ b
▲ Nachteil: Zusatzaufwand
G.37
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.2 Multiplikation für Zweierkomplement (4)
G.38
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.2 Multiplikation für Zweierkomplement (5)
■ Alternative C: getrennte Behandlung des Vorzeichens
■ Alternative D: Verfahren nach Booth
◆ Umwandlung der Faktoren in positive Zahlen
◆ Idee: a × 0111 = a × 1000 – a × 0001
◆ Berechnung des Ergebnisvorzeichens
• gilt auch für skalierte Bitfolge, z.B. a × 011100 = a × 100000 – a × 000100
◆ Anpassen des Ergebnisses
• Folge von 1-Bits lässt sich durch eine Addition und eine Subtraktion
multiplizieren
▲ Nachteil: Zusatzaufwand
◆ Algorithmus nach Booth
• betrachte alle Bits b i und gleichzeitig Bit b i – 1 ( b –1 wird als 0 definiert)
i
• ( bi, bi – 1 )2 = 01 2
addiere a × 2 (Beginn einer 1-Folge)
• ( bi, bi – 1 )2 = 10 2
subtrahiere a × 2 (Ende einer 1-Folge)
i
• ( bi, bi – 1 )2 = 00 2 oder ( b i, b i – 1 )2 = 11 2 tue nichts
G.39
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.40
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.2 Multiplikation für Zweierkomplement (6)
5.2 Multiplikation für Zweierkomplement (7)
■ Alternative D: Verfahren nach Booth
■ Alternative D: Verfahren nach Booth
◆ Subtraktion durch Addition des Zweierkomplements
◆ Beispiel: –2 x 3 = –6 (bei n = 4)
◆ gültige Ergebnisse auch für negative Zahlen (Zweierkomplement)
1110 x 00110
◆ n-Bit breiter Addierer ausreichend durch geschicktes Schieben
00000000
–1110
00100000
00010000
• Schiebeoperation mit Vorzeichenpropagierung
(Vorzeichen wird verdoppelt)
00001000
+1110
11101000
11110100
11111010
Start
00110
Shift
00110
Shift
00110
Shift
00110
Shift
111110102 = –6
G.41
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
5.2 Multiplikation für Zweierkomplement (8)
6 Binäre Division
■ Alternative D: Verfahren nach Booth
■ Papier- und Bleistift-Version
◆ Beispiel: 3 x –2 = –6
◆ Beispiel: 103 / 9 = ?
0011 x 11100
00000000
00000000
–0011
11010000
11101000
G.42
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
01100111 / 1001 = 1011
–1001
Quotient
00111
–1001
1110 Unterlauf / negatives Ergebnis
+1001 Korrektur
01111
–1001
01101
–1001
Rest
0100
Start
11100
Shift
11100
Shift
11110100
11100
Shift
11111010
1110
Shift
Kontrolle: 103 / 9 = 11 Rest 4
◆ Verfahren auch Restoring-Division genannt, da durch Korrektur ursprünglicher
Divident wiederhergestellt wird
111110102 = –6
G.43
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.44
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
6 Binäre Division (2)
6.1 Restoring Division
■ Mathematisch
■ Einsatz von Addition/Subtraktion und Schiebeoperationen
◆ Divident / Divisor = Quotient + Rest / Divisor
oder
Divident = Quotient x Divisor + Rest
◆ in jedem Schritt testweise Subtraktion des skalierten Divisors b
vom Dividenten a
• qi = 1 falls a – b ≥ 0
• qi = 0 und Korrektur falls a – b < 0
◆ häufig verlangt: Rest hat gleiches Vorzeichen wie Divident
◆ Nachholen signifikanter Ziffern zum Zwischenergebnis durch Schiebeoperation
◆ Überlauf möglich, wenn Quotient nicht so breit wie Divident
G.45
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
6.1 Restoring Division (2)
6.1 Restoring Division (3)
■ Serielles Dividierwerk für vorzeichenlose Zahlen
bn-1 ...
n
cout
b1
n
■ Vorzeichenbehaftete Division mit Zweierkomplement-Darstellung
◆ Verfahren im Prinzip identisch
b0
n-Bit-Addierer/
Subtrahierer
n
G.46
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
◆ jedoch:
add/sub
load q
q2n-1 ... qn+1 qn qn-1
...
• unterschiedliche Erkennung von Unterläufen
Steuerwerk
shift left q
q1
• Propagierung des Vorzeichens in oberer Hälfte von q beim Laden
q0
◆ lade q: obere Hälfte = 0, untere Hälfte = a (load q)
◆ n-mal:
• schiebe q nach links (shift left q)
• subtrahiere b von obere Hälfte q (sub):
negativ: q0 = 0 und addiere b zurück (add) / positiv: q0 = 1
◆ Ergebnis: obere Hälfte q = Rest, untere Hälfte q = Quotient
G.47
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/
G.48
© 2002-2007, Franz J. Hauck, Verteilte Systeme, Univ. Ulm, [2007s-TI1-G-Arith.fm, 2007-05-21 12.38] http://www-vs.informatik.uni-ulm.de/teach/ss07/ti1/