Die Statistik

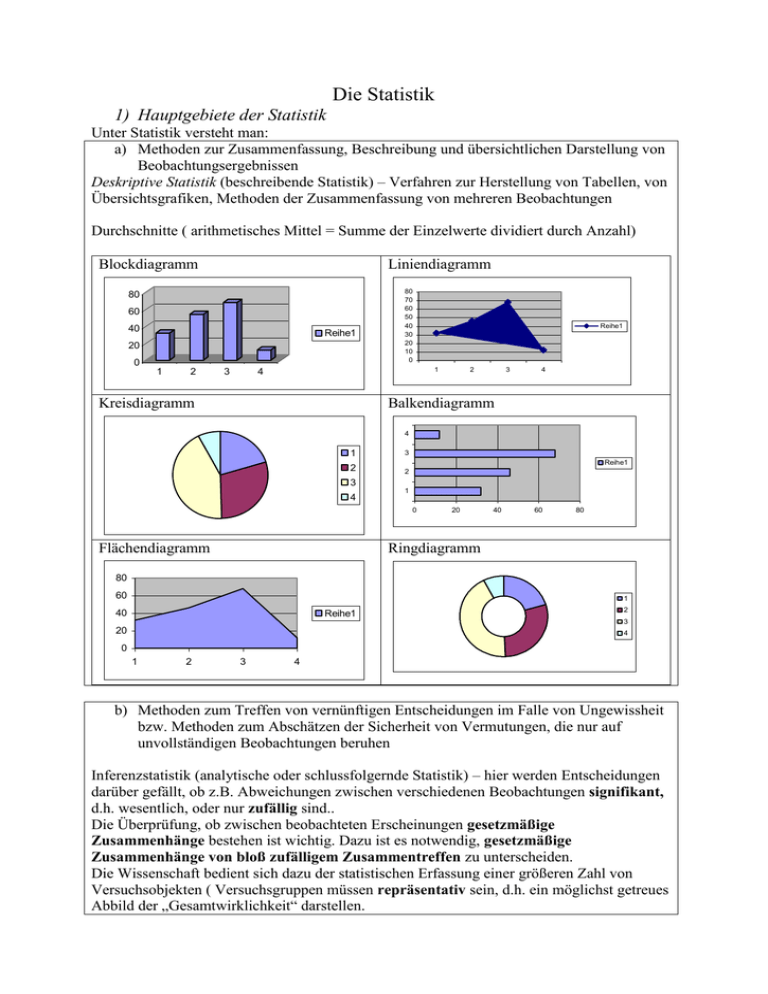
Die Statistik
1) Hauptgebiete der Statistik
Unter Statistik versteht man:
a) Methoden zur Zusammenfassung, Beschreibung und übersichtlichen Darstellung von
Beobachtungsergebnissen
Deskriptive Statistik (beschreibende Statistik) – Verfahren zur Herstellung von Tabellen, von
Übersichtsgrafiken, Methoden der Zusammenfassung von mehreren Beobachtungen
Durchschnitte ( arithmetisches Mittel = Summe der Einzelwerte dividiert durch Anzahl)
Blockdiagramm
Liniendiagramm
80
60
40
Reihe1
20
0
1
2
3
80
70
60
50
40
30
20
10
0
Reihe1
1
4
Kreisdiagramm
2
3
4
Balkendiagramm
4
1
3
2
2
Reihe1
3
4
1
0
Flächendiagramm
20
40
60
80
Ringdiagramm
80
60
1
40
Reihe1
2
3
20
4
0
1
2
3
4
b) Methoden zum Treffen von vernünftigen Entscheidungen im Falle von Ungewissheit
bzw. Methoden zum Abschätzen der Sicherheit von Vermutungen, die nur auf
unvollständigen Beobachtungen beruhen
Inferenzstatistik (analytische oder schlussfolgernde Statistik) – hier werden Entscheidungen
darüber gefällt, ob z.B. Abweichungen zwischen verschiedenen Beobachtungen signifikant,
d.h. wesentlich, oder nur zufällig sind..
Die Überprüfung, ob zwischen beobachteten Erscheinungen gesetzmäßige
Zusammenhänge bestehen ist wichtig. Dazu ist es notwendig, gesetzmäßige
Zusammenhänge von bloß zufälligem Zusammentreffen zu unterscheiden.
Die Wissenschaft bedient sich dazu der statistischen Erfassung einer größeren Zahl von
Versuchsobjekten ( Versuchsgruppen müssen repräsentativ sein, d.h. ein möglichst getreues
Abbild der „Gesamtwirklichkeit“ darstellen.
Ein gesetzmäßiger Zusammenhang wird in der Wissenschaft erst dann als erwiesen
angenommen, wenn die Wahrscheinlichkeit, dass es sich um ein zufälliges Zusammentreffen
handeln könnte, kleiner als 1% ( für weniger wichtige Zusammenhänge kleiner als 5% ist).
Ein solcher Zusammenhang, bei dem die Zufallswahrscheinlichkeit kleiner als 5% ist, wird
als statistisch signifikant, einer , bei dem sie kleiner als 1% ist, als sehr signifikant
bezeichnet.
In der Wissenschaft besteht auch großes Interesse für Zusammenhänge zwischen zwei (
oder mehreren ) Merkmalen. Solche Zusammenhänge werden Korrelation genannt.
Man unterscheidet positive Korrelationen und negative Korrelationen.
Diese Zusammenhänge können auch grafisch dargestellt werden.
Die Punkte im dadurch gegebenen zweidimensionalen Feld zeigen die Kombinationen an. Je
enger, schmäler der Punktschwarm ist, desto enger hängen die Merkmale zusammen. Die
Korrelation in Abb. 2 ist positiv : je mehr ... desto mehr ..., Abb. 3 negative Korrelation: je
mehr ... desto weniger ...
2) Wie fügt sich die Statistik in die übrigen wissenschaftlichen
Vorgangsweisen ein ?
Jede wissenschaftliche Untersuchung weist 4 Hauptstufen auf:
a) Beobachtung
b) Hypothese
c) Vorhersage und
d) Bestätigung
Ein einfaches Beispiel kann diese Punkte erläutern: Der berühmte Astronom Johannes Kepler
beobachtete die scheinbaren Planetenbahnen. Da diese nur schwer anders zu erklären waren,
stellte er die Hypothese (Annahme) auf, dass sich die Planeten und die Sonne nicht um die
Erde, sondern Erde und andere Planeten um die Sonne drehten. Aufgrund dieser Vermutung
erstellte er die Voraussage (Prognose), dass gewisse Sterne sich zu bestimmten Zeitpunkten
an bestimmten Orten befinden müssten, was sich dann auch durch neuerliche Beobachtungen
bestätigte (verifizierte). Wenn sich eine Annahme nicht bestätigt, spricht man von
Falsifizierung.
Die Statistik spielt dabei besonders für die Beobachtung und die Bestätigung eine große
Rolle. Sie zeigt, wie man sich mit einer Stichprobe (repräsentativen Gruppe) begnügen kann,
sie verhilft zur anschaulichen Beschreibung der Beobachtung (deskriptive Statistik), sie
sagt aber auch aus, wie wahrscheinlich eine bestimmte Aussage ist, ob bestimmte
Unterschiede zwischen den Beobachtungen nur zufällig oder wesentlich waren
(Inferenzstatistik)
Mag. Peter Mooslechner, Okt. 2003 (entnommen aus: Konecny: Lehrbuch der Psychologie)