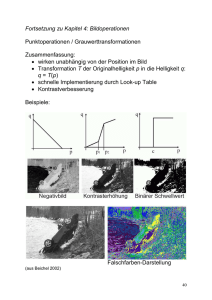
1 Allgemeine Einführung - RWTH Aachen University

Fraunhofer-Institut für
Lasertechnik ILT
Steinbachstrasse 15
52074 Aachen
Tel. 0241 8906 0
www.ilt.fraunhofer.de
Algorithmen zur Bildverarbeitung für die Prozessbeobachtung und regelung bei der Lasermaterialbearbeitung
Fachsemester 5
Aachen, den 8.12.2009
Name :
Frédéric Schulze
Matrikelnr.: 999524
Professor:
Dr. Wilhelm Hanrath
Betreuer:
Dr. Alexander Drenker
Unterschrift Auszubildender
Unterschrift Betreuer
Inhaltsverzeichnis
1
1.1
1.2
1.2.1
Allgemeine Einführung
Einleitung
Kameras und Licht
Belichtung
4
4
4
6
2
2.1
2.2
2.3
2.4
Störeinflüsse
Salt & Pepper Noise
Shot Noise
Gaussian Noise
Quantization Noise
7
7
7
7
8
3
3.1
3.2
3.2.1
3.2.2
3.2.3
Segmentierung von monochromen Bilder
Techniken der Segmentierung
Wahl eines geeigneten Schwellwerts
Manueller Schwellwert
Globale Schwellwertberechnung nach Otzu
Adaptive Schwellwertberechnung
9
9
9
9
10
11
4
4.1
4.1.1
4.1.2
4.1.3
4.1.4
4.2
4.2.1
4.2.2
4.2.3
Nachverarbeitung der segmentierten Bilder
Morphologische Basisoperatoren
Dilatation
Erosion
Opening
Closing
Weiterführende morphologische Operatoren
Randerkennung
Distanztransformation
Der Hit or Miss Operator
12
12
12
12
13
13
14
14
14
15
5
5.1
5.2
5.3
5.3.1
5.3.2
5.3.3
Auswertung der Binärbilder
Nachbarschaften von Pixeln
Region Labelling
Eigenschaften der Regionen
Flächenberechnung
Schwerpunktsberechnung
Kreisförmigkeit
15
15
15
16
16
16
17
6
6.1
Orts- und Frequenzraum
Transformationen für die Bildbearbeitung
17
17
2
6.2
6.3
6.4
6.5
6.6
6.6.1
6.6.2
6.6.3
Fourier Transformation
Fast Fourier Transformation
Faltungen
Korrelationen
Filter
Durchschnittsfilter
Gaußfilter
Medianfilter
18
21
21
22
23
23
25
27
7
Kanten und Ableitungen
28
8
8.1
8.2
8.3
8.4
8.5
Anwendungen im Institut für Lasertechnik
Geschwindigkeitsmessung mittels Kreuzkorrelation
Nahtfolgeerkennung mittels Konturerkennung
Referenzfilmvergleich mittels Kreuzkorrelation
Zählungen von Pulververteilungen
Intensitätsverteilungen beim Laserbohren
29
29
29
30
30
30
9
Zusammenfassung
31
3
1
Allgemeine Einführung
1.1
Einleitung
Diese Seminararbeit bietet eine Einführung in die Grundlagen der digitalen Bildverarbeitung und stellt Algorithmen für die Verarbeitung von
monochromen Bildern vor. Der Bezug zur praktischen Anwendungen wird durch Beispiele aus dem Bereich der Lasertechnik hergestellt.
Vorgestellt werden verschiedene Algorithmen zur Segmentierung, Nachverarbeitung und Auswertung von Bildern. Die Wirkungsweise wird an
Hand von Beispielen in erklärenden Abbildungen gezeigt. Des Weiteren wird auf Einsatzgebiete und Vorteile verschiedener Transformationen
eingegangen. Außerdem wird auf die Funktionsweise eines optischen Aufnahmesystem und das Auftreten verschiedener Störeinflüsse und
dafür geeignete Filter eingegangen. Die Bedeutung von Ableitungen zur Kantenerkennung wird ebenfalls kurz erläutert.
1.2
Kameras und Licht
Ebenso wie das menschliche Auge sind Kameras mit Halbleiter-Bildsensoren (CCD, CMOS) durch den Bereich ihrer spektralen
Empfindlichkeit charakterisiert. Das menschliche Auge nimmt auch nur einen kleinen Bereich des elektromagnetischen Spektrums wahr. Ein
Mensch kann weder ultraviolettes noch infrarotes Licht sehen, da einerseits die Linse seines Auges im UV-Bereich nicht transparent ist und
andererseits die Rezeptoren in der Netzhaut seines Auges in diesen Wellenlängenbereichen unempfindlich sind.
Bild 1 Wellenlängen- und Frequenzbereich des Lichts
4
Kameras verfügen über einen Verschlussmechanismus über den ihre Belichtungszeit gesteuert wird [2]. Im Belichtungszeitintervall sammelt
die Kamera Photonen ihres Wellenlängenbereiches auf ihrem Sensorchip und wandelt diese in Fotoelektronen um. Um diese Elektronen zu
erzeugen wird bei Halbleiter Bildsensoren eine Photodiode eingesetzt die einen Kondensator lädt. Für jedes Belichtungsintervall wird der
Kondensator neu geladen. Am Ende des Intervalls wird die Ladung des Kondensators über einen A/D Wandler abgetastet und als digitaler
Wert der entsprechenden Intensität abgebildet. Jeder Pixel des Bildsensors wird über eine solche Schaltung realisiert [3]. Anschließend
werden die Kondensatoren entladen und die abgetasteten Intensitäten gespeichert oder zu einem Verarbeitungsrechner übertragen [4]. Bei
der Übertragung von Kameradaten zu Computer ist „CameraLink“ der momentane Industriestandard. Für die in dieser Arbeit untersuchten
Algorithmen zur Bildverarbeitung genügt es sich den bildgebenden Sensor als zweidimensionales Feld vorzustellen.
Bild 2 Verschlusszustände der Kamera
Bild 3 Prinzipschaltbild eines Pixel
Bild 4 Datenübertragung zum Computer
Eine RGB Kamera nimmt Licht in drei verschiedenen Wellenlängenbereichen auf. Jeder Wellenlängenbereich wird in einem eigenen Farbkanal
gespeichert. Die einzelnen Felder des Sensorchips bestehen hierzu wiederum aus einem kleinen zweidimensionalen Feld. Eine bestimmte
Anzahl dieser Teilfelder nimmt dann jeweils rotes, grünes oder blauen Licht war. Die auf den Teilfeldern gezählten Photonen bestimmten die
Intensität des jeweiligen Farbkanals. Aus den Intensitäten der drei Farbkanäle wird schließlich die Farbe des dargestellten Pixels gemischt.
Die allgemein bekannten Farbkameras arbeiten mit dieser Technik.
5
Bild 5 Sensorchip mit Pixelausschnitt
Bild 6 Bayermatrix mit Darstellung der einzelnen Farbkanäle
Monochromatische Kameras nehmen hingegen immer nur einen Wellenlängenbereich des Lichts war und verfügen daher auch nur über einen
Farbkanal. Die Felder des Sensorchips sind daher nicht in Teilfelder aufgeteilt, sondern zählen nur die absorbierten Photonen, deren
Wellenlänge im Bereich der spektralen Empfindlichkeit des Sensors liegt. Die Anzahl der gezählten Photonen beschreibt also die Intensität des
dargestellten Grauwertes. Diese Kameras, wie zum Beispiel Infrarotkameras finden in der industriellen Bildverarbeitung ihren Haupteinsatz.
1.2.1
Belichtung
Über- und unterbelichtete Bilder kommen dadurch Zustande, dass zu viele oder zu wenige Photonen während des Belichtungszeitintervalls im
Wellenlängenbereich der Kamera eingefangen wurden. In solchen Fällen sollte die Belichtungszeit entsprechend reduziert bzw. erhöht
werden, um eine gleichmäßigere Intensitätsverteilung des Bildes zu gewährleisten. Sollten trotz der kleinst möglicher Belichtungszeit zu viele
Photonen auf den Sensorchip ankommen, lässt sich der Photonenfluss über Graufilter oder verkleinerte Blendenöffnungen abschwächen.
Letzteres vergrößert die Schärfentiefe zu Lasten des Auflösungsvermögens.
Die Farbtiefe einer Kamera beschreibt die Anzahl der verschiedenen darstellbaren Intensitäten. Die Anzahl der Intensitätstuffen berechnet sich
aus zwei hoch der Farbtiefe. Eine 8 Bit Kamera hat also 256 Intensitätstuffen. Bei einem monochromen Bild repräsentieren die Intensitätstuffen
6
die unterschiedlichen Grauwerte der Pixel und bei einem RGB Bild die verschiedenen Helligkeiten des jeweiligen Farbkanals eines Pixels.
Kameras mit höheren Farbtiefe unterteilen ihre Abbildung also deutlich feiner.
2
Störeinflüsse
2.1
Salt & Pepper Noise
Diese Form des Rauschens kennzeichnet sich durch das Auftreten von weißen und schwarzen Pixeln. „Salt & Pepper Noise“ wird durch
Bitfehler auf dem Übertragungsweg verursacht. Die Bitfehler auf dem Übertragungsweg werden durch sich in die Übertragung einkoppelnde
Störfrequenzen verursacht. Das hochfrequente Störsignal induziert durch sein elektromagnetisches Feld eine Spannung in den Leiter,
wodurch eine impulsartige Signalverfälschung erfolgt. Deswegen wird diese Rauschform auch häufig als Impulsrauschen bezeichnet.
Bild 7 Salt & Pepper Noise
2.2
Shot Noise
„Shot Noise“ wird durch die Fluktuation der gezählten Photonen verursacht. Bei dunklen Bildern ist die Fluktuation in der Regel höher als bei
einer gut ausgeleuchteten Szene. Die „Shot Noise“ tritt zufällig auf und lässt sich über eine Passion Verteilung beschreiben. Bei Bildern mit
hoher Auflösung ergibt sich ein großer Stichprobenumfang und die Passion Verteilung kann über eine Gaußverteilung genähert werden.
2.3
Gaussian Noise
Das Rauschen ist gleichmäßig über die Abbildung verteilt und ist unabhängig von der Signalintensität des Bildes. Gaußförmiges Rauschen
wird primär durch das thermische Rauschen des Aufnahmesystems und Rauschanteile, die beim entladen der Kondensatoren entstehen
verursacht.
7
Bild 8 Gaussian Noise
2.4
Quantization Noise
Diese Art des Rauschens wird durch Signalschwankungen um die Quantisierungsstuffen des Aufnahmesystems verursacht. Schon bei
leichten Schwankungen muss sich der A/D Wandler bei der Abtastung des Signals zwischen zwei Intensitäten entscheiden. Dieser Effekt lässt
das Bild schließlich verrauscht erscheinen. Die mittlere Abweichung zum eigenlichten Wert entspricht also immer der halben Länge einer
Quantisierungsstuffe. Wenn das Aufnahmesystem seinen Bereich des elektromagnetischen Spektrums gröber quantisiert erhört sich die
mittlere Abweichung der analogen Werte entsprechend und die Rauschanteile nehmen proportional zu.
Bild 9 Beispiel eines Quantisierungsschemas
8
3
Segmentierung von monochromen Bilder
3.1
Techniken der Segmentierung
Bild 10 Aufbau eines Binärbildes
Der Konvertierungsalgorithmus schaut sich jedes Pixel des Graubildes an und setz es unter Berücksichtigung eines Schwellwertes auf einen
binären Wert. Es wird hierbei zwischen drei verschiedenen Techniken unterschieden. Bei der einseitigen Betrachtung werden alle Pixel mit
Intensitäten oberhalb des Schwellwertes auf eins gesetzt und alle anderen auf null. Bei der zweiseitigen Betrachtung müssen sich die
Intensitäten der Pixel in einem Schwellwertintervall befinden um auf eins gesetzt zu werden. Alle außerhalb des Intervalls werden auf null
gesetzt. Die dritte Möglichkeit ist es eine Liste diskreter Werte an zugeben und anschließend das Bild nach diesen zu segmentieren. Mit
diesen Techniken lassen sich sehr gut Objekte von Hintergrund segmentieren.
1, wenn F i, j   T
FT [i, j ]  
0, sonst
1, wenn T1  F [i, j ]  T2
1, wenn F [i, j ]  
FT [i, j ]  
FT [i, j ]  
0, sonst
0, sonst
Einseitig
Bild 11 Original
3.2
Wahl eines geeigneten Schwellwerts
3.2.1
Manueller Schwellwert
Zweiseitig
Diskrete Werte
Bild 12 Segmentiert
Der Schwellwert kann manuell festgelegt werden. Hierzu empfiehlt es sich das Histogramm des Bildes zu betrachten [Abbildung 11].
9
Bild 13 Graubild
Bild 14 Histogramm
Bild 15 Binärbild
Der große Peak des Histogramms [14] sind die Grauwerte des helleren Hintergrunds [13]. Der kleine Peak umfasst die Helligkeitswerte des
dunklen Rechtecks. Wird der Schwellwert aus dem Bereich zwischen den beiden Peaks gewählt so lässt sich das Rechteck gut vom
Hintergrund segmentieren [15]. Außerdem gibt es die Möglichkeit einen geeigneten Schwellwert automatisiert zu berechnen. Hierbei wird
zwischen globalen und lokalen Methoden unterschieden. Im Folgenden wird jeweils eine gängige Methode aus beiden Bereichen vorgestellt.
3.2.2
Globale Schwellwertberechnung nach Otsu
Bei der globalen Schwellwertberechnung werden aus den Pixelhelligkeiten des gesamten Bildes zwei Intensitätsverteilungen berechnet, durch
die sich die abgebildete Szene möglichst klar unterscheiden lässt. Um diese Verteilungen zu errechnen ist es nötig die zufällig auftretenden
Intensitäten der Pixel in geeigneter Weise zu beschreiben. Da sich bei einer Berechnung über ein Gesamtbild eine große Anzahl an Pixeln
ergibt, eignet sich die gaußsche Normalverteilung sehr gut zur näherungsweisen Beschreibung dieses Verhaltens. Das im Jahr 1979 von
Nobuyuki Otsu entwickelte Verfahren beschreibt die Streuung der Grauwerte auf Basis der gaußschen Normalverteilung und ist deshalb das
quasi Standardverfahren zur globalen Schwellwertberechung. Prinzipiell wird eine Verteilung der Grauwerte unterhalb eines freiwählbaren
Schwellwertes und eine Verteilung oberhalb des Schwellwertes berechnet. Anschließend wird die Interne- und die Zwischenvarianz dieser
beiden Verteilungen bestimmt. Die Zwischenvarianz beschreibt den Abstand zwischen den beiden Verteilungen und die interne Varianz
drückt ihre Ähnlichkeiten aus. P(g) ist die Auftrittswahrscheinlichkeit der Grauwerte.
t
K o : Po (t )   p( g )
K1 : P1 (t ) 
g 0
Wahrscheinlichkeit <= T
t
 p( g )
g t 1
 1  P0 (t )
Wahrscheinlichkeit > T
g 0 und g 1 sind die arithmetischen Mittel der beiden Verteilungen.
t
 02 (t )   ( g  g 0 ) 2 p( g )
 12 
g 0
Varianz der ersten Verteilung
t
 (g  g )
g t 1
1
2
p( g )
Varianz der zweiten Verteilung
10
Die interne Varianz ergibt sich aus der Summe der Einzelvarianzen gewichtet mit der Gesamtwahrscheinlichkeit der Grauwerte innerhalb einer
der beiden Verteilungen zu liegen.
 in2 (t )  P0 (t ) *  02 (t )  P1 (t ) *  12
Interne Varianz
Die Zwischenvarianz ergibt sich aus der Summe von zwei Verteilungsfaktoren. Der Faktor einer Verteilung berechnet sich aus den
quadratischen Abständen ihres Mittelwerts zum Mittelwert des Bildes und einer Gewichtung mit der Wahrscheinlichkeit der Lage aller
Grauwerte innerhalb dieser Verteilung.

2
zw
 P0 (t ) * ( g 0  g )  P1 (t ) * ( g1  g )
2
Zwischenvarianz
2
2
 zw
(t )
Q(t )  2
 in (t )
Quotient der Varianzen
Anschließend wird ein Quotient aus der Zwischen- und Inneren Varianz gebildet. Dieser Quotient erreicht sein Maximum, wenn die
Zwischenvarianz möglichst groß und die interne Varianz möglichst gering ist. Ziel ist es also die zwei gaußschen Normalverteilungen zu finden
deren eigene Varianzen am geringsten sind, aber gleichzeitig die größtmögliche Gesamtvarianz besitzen. Um diesen Grauwert zu finden wird
der Schwellwert entlang des Farbraumes inkrementiert und anschließend der Grauwert ausgewählt, der den größten Quotienten besitzt. Eine
sinnvolle Optimierung ist es sicher unter Betrachtung des Histogramms den Schwellwert nur über die relevanten Teile des Intensitätsbereiches
zu inkrementieren.
3.2.3
Adaptive Schwellwertberechnung
Die adaptive Schwellwertberechnung wird oft auch als lokale oder dynamische bezeichnet. Es wird eine Struktur über das Bild bewegt und für
jede neue Position der Struktur wird ein lokaler Schwellwert bestimmt mit dem dann der Bildausschnitt unterhalb der Struktur segmentiert wird.
Auch hier gibt es mehrere Verfahren. Die einfachste Möglichkeit ist es den Median oder den Durchschnitt der Pixel als lokalen Schwellwert zu
verwenden. Dies funktioniert gut, weil alle zur Berechnung beitragenden Pixel einen Mittelwert ergeben der sich zwischen Hintergrund und
Objekt befindet, sofern diese sich von ihrer Intensität deutlich unterscheiden. Sollte dieser Unterschied auf Grund von Rauschen oder anderen
Störgrößen jedoch undeutlich sein so versagen diese Verfahren. In einem solchen Fall empfiehlt es sich ein iteratives Verfahren zu verwenden.
Die großen Vorteile eines solchen Verfahrens sind, dass es sehr robust gegen Störeinflüsse ist und die Qualität des Schwellwerts über die
Anzahl der Iterationen gesteuert werden kann. Zunächst wird empirisch eine Startschwellwert bestimmt und es werden die Durchschnitte der
Pixel kleiner gleich dem Schwellwert und oberhalb des Schwellwertes berechnet. Der neue Schwellwert ist der Mittelwert der beiden
Durchschnitte. Anschließend wird das Verfahren unter Verwendung des in der vorherigen Iteration berechten Schwellwertes solange
wiederholt bis sich der errechnete Schwellwert nicht mehr vom vorherigen unterscheidet oder eine vorgegebene maximale Anzahl an
Iterationen erreicht ist. Eine maximale Iterationsanzahl ist nur dann sinnvoll, wenn die Schwellwerte mit gleichbleibendem Rechenaufwand
bestimmt werden sollen, da dies zu schlechteren Segmentierungsergebnissen führen kann.
11
Bild 16 Original
Bild 17 Global
4
Nachverarbeitung der segmentierten Bilder
4.1
Morphologische Basisoperatoren
Bild 18 Lokal
Morphologische Operatoren bewirken Umformungen im Bild. Die grundlegenden morphologischen Transformationen werden als Dilatation
and Erosion bezeichnet. Sie eignen sich zur Nachverarbeitung der segmentierten Bilder. Hauptsächlich werden sie zum Filtern von Rauschen
und zum Isolieren beziehungsweise Verbinden von nahegelegenen Objekten eingesetzt. Die generelle Idee ist es eine Struktur mit einem
Befestigungspunkt über ein Bild zu verschieben und die unterliegenden Pixel zu glätten. Im Folgenden wird zur Erklärung der verschiedenen
Operatoren von einer rechteckigen Struktur mit einem zentralen Befestigungspunkt ausgegangen.
4.1.1
Dilatation
Bei der „Dilatation“ wird für jede Position der Struktur auf dem Bild die maximale Intensität ermittelt. Die Pixel unterhalb des
Befestigungspunktes der Struktur werden auf das lokale Maximum gesetzt und die Struktur wird weiter auf dem Bild verschoben. Dieses
Verhalten versucht eine Vergrößerung der Objekte und eignet sich deshalb gut zum Füllen von Löchern, die oft bei der Segmentierung des
Bildes entstehen oder zum Verbinden von zerteilten Objekten.
4.1.2
Erosion
Bei der „Erosion“ wird für jede Position der Struktur auf dem Bild die minimale Intensität ermittelt. Die Pixel unterhalb des Befestigungspunktes
der Struktur werden auf das lokale Minimum gesetzt und die Struktur wird weiter auf dem Bild verschoben. Diese Verhalten führt versucht eine
Verkleinerung der Objekte und eignet sich dadurch besonders gut zum filtern von Rauschen.
12
Bild 19 Original
4.1.3
Bild 20 Dilataion
Bild 21 Erosion
Opening
Der Begriff „Opening“ beschreibt eine Sequenz der „Erosion“ und „Dilation“. Damit wird zunächst das Rauschen entfernt und die beim Filtern
des Rauschens entstehenden Löcher und zerteilen Objekte wieder aufgefüllt bzw. verbunden. Diese Technik wird oft zum Zählen von Objekte
in Binärbildern eingesetzt.
4.1.4
Closing
Der Begriff „Closing“ beschreibt eine Sequenz der „Dilation“ und „Erosion“. Es werden zunächst die nahegelegenen Objekte miteinander
verbunden und die Löcher innerhalb der Objekte gefüllt. Anschließend wird das übrig gebliebene Rauschen, das während der „Dilation“
keinem Objekte zugeordnet werden konnte entfernt.
Bild 22 Fingerabdrucksscan mittels Opening & Closing
13
4.2
Weiterführende morphologische Operatoren
Morphologische Operatoren eignen sich nicht nur zur Nachverarbeitung segmentierter Bilder, sondern auch zur Formerkennung. Im
Folgenden werden zwei einfache Operatoren auf Basis der Dilatation und Erosion zur Bestimmung des Objektrandes und
Distanztransformation vorgestellt.
4.2.1
Randerkennung
Bei der Randerkennung wird das Bild zunächst erodiert und somit die Ränder der Objekte abgetragen. Anschließend wird vom Originalbild
das Erodierte abgezogen und als Differenz bleiben die im erodierten Bild abgetragen Ränder der Objekte.
Bild 23 Original
4.2.2
Bild 24 Ränder
Distanztransformation
Bei der Distanztransformation wird der kürzeste Abstand jedes Pixels eines Objekts zu seinem Rand bestimmt. Er wird zunächst eine
Randerkennung durchgeführt um die Lage des Randes zu ermitteln. Danach erodiert man das Originalbild iterationsweise solange bis das
untersuchte Objekt vollständig verschwunden ist. In jedem Iterationsschritt wird als Distanz zum Rand für jedes der gerade entfernten Pixel die
Iterationskonstante in einem Graubild gespeichert. Das dadurch entstehende Graubild zeigt einen ansteigenden Intensitätsverlauf zu
Objektmitte. Mittels linearer Interpolation zwischen den Distanztransformationen verschiedener Objekte lassen sich die Objekte in einander
umformen.
14
4.2.3
Der Hit or Miss Operator
Durch morphologische Operatoren lassen sich nicht nur einfache Strukturen, sondern auch komplexere Geometrien erkennen. Der
grundlegende Operator zur Erkennung solcher Geometrien ist der „Hit-or-Miss-Operator“. Der „Hit-or-Miss-Operator“ besteht aus zwei
Erosionsschritten, bei denen mit unterschiedlichen Erosionsstrukturen gearbeitet wird und einer anschließenden Und- Verknüpfung der
beiden Ergebnisse. Als Ergebnis des Operators entsteht ein Bild in dem alle Instanzen der gesuchten Geometrie zusehen sind. Der erste
Erosionsschritt wird als Hit Schritt bezeichnet. Es wird zunächst eine Erosionsstruktur erstellt, die der gesuchten Geometrie entspricht. Bei
dieser Operation werden alle Elemente gelöscht, die kleiner als das Muster sind. Übrig bleiben nur die Strukturen die größer als das
Suchmuster sind. Dadurch entsteht ein Bild, das alle Objekte der Szene enthält, die dem Suchmuster entsprechen. Der zweite Erosionsschritt
wird als Miss Schritt bezeichnet. Als Erosionsstruktur wird ein Muster verwendet, das den Hintergrund des gesuchten Objektes darstellt. Diese
Operation wird auf dem negierten Bild der Szene ausgeführt, damit alle Objekte gefunden werden, um die sich der gesuchte Rand
positionieren lies. Durch die Und- Verknüpfung werden nun die möglichen Lagen der Struktur und die Positionierungsmöglichkeiten des
Hintergrunds miteinander verglichen.
5
Auswertung der Binärbilder
5.1
Nachbarschaften von Pixeln
Bild 25 4er Nachbarschaft
5.2
Bild 26 8er Nachbarschaft
Region Labelling
Das Region Labelling ist eine Technik um die unterschiedlichen Objekte des segmentierten Binärbildes zu klassifizieren. Der Algorithmus geht
über das Binärbild und gibt jedem Objekte, dass durch eine Eins repräsentiert wird einen neuen Grauwert oder Farbwert. Bei Region Labelling
mit 4er Nachbarschaft wird nur auf den Hauptachsen nach Bestandteilen des Objektes gesucht und bei einer 8er Nachbarschaft werden
zusätzlich die Diagonalen übergeprüft. Zunächst wird das Bild von links nach rechts und anschließend von oben nach unten bearbeitet, dabei
wir eine Tabelle mit Vektoren der verschiedenen Labels angelegt. Diese Tabelle ist nötig, damit während des Bilddurchlaufes keine Labels
geändert werden müssen. Ist zum Beispiel ein Objekt in einer Bildzeile gefunden worden und ergeben sich bei der Spaltensuche zwei neue
Objekte, die aber in dem Objekt der Bildzeile enden und damit auch nur zu einem gehören, dann wird einfach ein weiterer Wert in den Vektor
des Labels eingetragen. Die Anzahl verschieden Vektoren der Labeltabelle entspricht der Anzahl der verschiedenen Objekte. Das Region
Labelling eignet deshalb auch sehr gut zum zählen von Strukturen. Anschließend wird in einer Nachverarbeitung jeder Labelvektor durch
15
einen festen Wert ersetzt. Das daraus entstehende Bild stellt die einzelnen Objekte in einem anderen Grauwert bzw. Farbton dar, wodurch sie
sich sehr gut unterscheiden lassen.
Bild 27 Binärbild
Bild 28 Grauwerte
5.3
Eigenschaften der Regionen
5.3.1
Flächenberechnung
Bild 29 Farben
Die Größe eines Pixels ergibt sich aus dem Verhältnis der Auflösung zur Größe des Sensorchips. Demnach ist die Fläche einer Region die
Summe der Größen, der zu ihr gehörenden Pixel. Diese Fläche ist aber leider nur die Größe mit der das Objekt im Bild dargestellt wird. Um
also die tatsächliche Fläche des realen Objektes bestimmen zu können muss der Vergrößerungsmaßstab des Aufnahmesystems bekannt
sein, damit die Pixelgrößen in Streckeninformationen transformiert werden können.
A
1
( x, y )
Flächenformel
5.3.2
Schwerpunktsberechnung
Die Lage in X Richtung ergibt als Kehrwert der Regionsfläche multipliziert mit der Summe aller X Koordinaten, der zur Region gehörenden
Pixel. Die Lage des Schwerpunktes in Y Richtung errechnet sich analog. Natürlich sind hierbei die Y Koordinaten der Pixel zu verwenden.
X 
1
x
A ( x, y )
Schwerpunkt X
Y 
1
y
A ( x, y )
Schwerpunkt Y
16
5.3.3
Kreisförmigkeit
Die Kreisförmigkeit eines Objektes wird anhand der Ähnlichkeit einer Region zu einem echten Kreis gemessen. Die Kreisförmigkeit ergibt sich
als Quotient des Mittelwerts der radialen Entfernung und der Wurzel der Varianz der radialen Entfernung. Der Begriff der radialen Entfernung
beschreibt den Abstand vom Rand einer Region bis zum ihrem Schwerpunkt. Der Mittelwert der radialen Entfernung wird aus der Summe der
Beträge des Abstands aller Randpixel zum Schwerpunkt berechnet. Die Varianz ist dann die Summe der quadratischen Abweichungen der
jeweiligen Randdistanz im Vergleich zum errechneten Mittelwert. Umso näher der Quotient der Kreisförmigkeit an Eins liegt umso ähnlicher ist
die untersuchte Region einem Kreis.
R 
Mittelwert
1
K
K 1
 (x
k 0
k
, yk )  ( x, y)
Varianz
6
Orts- und Frequenzraum
6.1
Transformationen für die Bildbearbeitung
 R2 
1
K
K 1
  (x
k 0
, yk )  ( x, y) 
2
k
C
R
R
Quotient
Bei einer Abbildung im Ortsraum wird das Bild als eine diskrete Funktion der Intensitäten dargestellt. Im Frequenzraum hingegen wird das Bild
als eine Kombination der Frequenzen der verschiedenen elektromagnetischen Wellen abgebildet. Darstellungen im Frequenzraum sind für die
Bildverarbeitung in verschiedenen Anwendungsbereichen von Interesse. Zum Beispiel können die im Folgenden erklärten Faltungen und
Korrelationen dort wesentlich effizienter ausgeführt werden. Ein anderer wichtiger Aspekt ist die Komprimierbarkeit der Abbildungen, die an
Hand einer frequenzbasierten Darstellung erheblich vereinfacht und verbessert wird. Um ein Bild in den Frequenzraum zu überführen wird
eine geeignete Transformationsmethode benötigt. Die Transformationen müssen für jedes Bild eine eindeutige Darstellung ermöglichen und
vollständig umkehrbar sein, damit die durch Bearbeitung im Frequenzraum erzielten Ergebnisse wieder in den Ortsraum zurück transformiert
werden können. Die Bilder können dazu als zweidimensionale, diskrete Funktionen mit beschränktem Definitions- und Wertebereich
aufgefasst werden. Werden die Zeilen des Bildes in einen Vektor hintereinander geschrieben, dann kann die Transformation durch eine
einfache Multiplikation mit einer Transformationsmatrix realisiert werden. Um eine eindeutige Darstellung aller Bilder zu ermöglichen muss eine
Transformationsmatrix bestehend aus N linear unabhängigen Funktionen gefunden werden. Die linear unabhängigen Funktionen spannen
dann eine Basis im alternativen Raum auf. Eine Rücktransformation in den Ortsraum entspricht dann einer Matrixmultiplikation mit der inversen
Transformationsmatrix. Da im Allgemeinen die Berechnung einer Inversen aufwändig ist, sind vor allem orthogonale Basen interessant, da hier
die Inverse der Transponierten der Transformationsmatrix entspricht. Dadurch werden die Rücktransformationen in den Ortsraum erheblich
vereinfacht und lassen sich wieder auf eine einfache Matrixmultiplikation mit der transponierten Transformationsmatrix zurückführen. Jede
Zeile dieser Transformationsmatrix beinhaltet eine Basisfunktion der neuen Basis. Wie auch bei Vektorbasen gibt es keine eindeutige Basis,
die den gesamten Raum beschreibt, sondern es können immer verschiedene Basen gefunden werden. Es können also immer M Basen
17
gefunden werden, unter denen wiederum N Orthogonalbasen existieren. Für die Bildverarbeitung sind jedoch nur die Orthogonalbasen von
Interesse, deren alternative Darstellungen eine qualifizierte Aussage über das jeweilige Problem erlauben. Es gibt mehrere bekannte
orthogonal Basen die eine geeignete Darstellung im Frequenzraum ermöglichen. Die Fourier Basis beseht aus komplexen, periodische
Basisfunktionen, die Bildfrequenzen als eine Kombination aus Sinus- und Kosinusthermen abbildet. Die Fourier- Transformation wird
hauptsächlich zur Bearbeitung von Bildern eingesetzt. Die Kosinusbasis beschreibt die Frequenzen des Bildes als eine Folge Kosinusthermen
und Wavlet Basen bilden die Bildfrequenzen in Form von Basis- und Skalierungswavelts ab und sind vor allem für die Bildkomprimierung von
Interesse. Ein Wavlet ist eine Schwingungsfunktion die nur in einem kleinen Intervall ihres Definitionsbereiches eine Amplitude besitzt. Durch
die Skalierungswavlets wird der Ortsraum des Bildes in kleine Teilstücke zerlegt, deren Frequenzbereich dann als eine Kombination aus sich
überlappender Wavlets modelliert wird [30]. Dieser Vorteil der räumlichen Separierbarkeit der Wavelettransformation ist vor allem bei der
Bildkompression von großem Vorteil, da nun abhängig vom Ort Frequenzen, die keine oder nur wenige Informationen transportieren
ausgelöscht werden können. Bei den anderen Transformationsmethoden transportieren die Frequenzen jedoch Informationen des gesamten
Bildes. Auch hier können natürlich die informationsschwachen Frequenzen ausgelöscht werden, doch ist es leicht einzusehen, dass bei einem
realen Bild die Frequenzen meist eher lokal wirken, als über den gesamten Bildbereich und deshalb eine lokales Löschen der unrelevanter
Frequenzen das Originalbild bei gleicher Informationsreduktion deutlich weniger verfälscht.
Bild 30 Räumliche Separierbarkeit der Wavlettransformation
6.2
Fourier Transformation
Für Störfrequenzen gilt jedoch, dass sie meist gleichmäßig über das Bild verteilt sind und damit keine örtliche Lokalität besitzen. Aus diesem
Grund eignet sich die Fourier-Basis besonders gut für eine Filterung von Störgrößen. Es empfiehlt jedoch die Komponenten der FourierTransformation als Eulerzahlen darzustellen, da dies den Vorteil hat, dass die Amplitude und Phase einer Welle in einer einzigen Zahl kodiert
sind. Die Amplitude einer Welle beschreibt die Grauwertvariation, des durch sie verursachten Bildanteils. Deswegen lässt sich das
Intensitätsspektrum des Bildes sehr gut über die Amplituden der verschiedenen Wellen steuern. Wird beispielsweise die Amplitude aller
Wellen eines Bildes halbiert, dann ist es anschließend nur noch halb so hell. Für eine visuelle Darstellung des Frequenzraumes gibt es zwei
Möglichkeiten. Zum einen besteht die Möglichkeit der Erzeugung eines Amplitudenbilds, das die Beträge der komplexen Zahlen aller Wellen
darstellt. Das Amplitudenbild bildet also die reellen Anteile der Wellen ab. Auf der anderen Seite besteht die Möglichkeit der Erzeugung eines
18
Phasenbildes. Das Phasenbild stellt jedoch die Winkel der Wellen zur reellen Achse dar und bildet demnach den imaginären Anteil der Wellen
ab. Meist wird jedoch nur eine Amplitudenbild erzeugt, weil es das oftmals aussagekräftigere Spektrum des Bildes beschreibt. Bei der
Erzeugung des Amplitudenbilds wird der Ursprung in den Mittelpunkt verschoben, damit die niedrigen Frequenzen in der Bildmitte zu sehen
sind.
Bild 31 Darstellung der Amplitude (Original und Amplitudenbild Oben,
dezentrales und zentrales logarithmiertes Amplitudenbild Unten)
Bild 32 Amplitudenbilder verschiedener Objekte
19
Bei räumlich separierbaren Transformation wird die Abbildung zunächst örtlich zerlegt und anschließend für jeden Ort ein Phasen oder
Amplitudenbild nach dem zuvor beschrieben Vorgehen erzeugt. Für die meisten Bilder sinken die Werte der Amplitude mit steigender
Frequenz sehr schnell ab. Der Abfall ist meist sogar so stark, dass bei der Abtastung der reellen Amplitudenwerte der Wellen die meisten Pixel
auf Null abgebildet werden, weshalb meistens eine logarithmierte Darstellung des Amplitudenbilds bevorzugt wird [31]. Der relativ schnelle
und starke Abfall der Amplituden bei steigender Frequenz bedeutet, dass in den meisten Bildern ein erhebliches Kompressionspotential
steckt. Da niedrige Amplituden eine geringe Variation der Grauwerte im Ortsbereich bedeuten, ist der Informationsverlust durch Streichung der
Wellen mit geringen Amplituden kaum wahrnehmbar. Die Wellen enthalten jedoch nicht nur Informationen über die Grauwertvariationen der
Objekte einer Szene, sondern auch über ihre Lage im Ortsraum. Die Verschiebung eines Objektes im Ortsraum entspricht beispielsweise einer
Phasenverschiebung im Frequenzraum bei gleich bleibender Amplitude [33].
Bild 33 Translationsbewegung
Die Rotation eines Objektes hingegen entspricht einer Drehung der Amplitude ohne eine Phaseverschiebung zu bewirken [34]. Aus der
Feststellung das niedrige Frequenzen meist eine hohe Amplitude besitzen und umgekehrt lässt sich die allgemeine Aussage ableiten, dass
die hochfrequenten Anteile des Bildes meistens einen geringeren Informationsgehalt der Szene transportieren.
20
Bild 34 Rotationsbewegung
6.3
Fast Fourier Transformation
Nahezu jede Bildverarbeitungsbibliothek enthält eine schnell berechende Variante der Fourier-Transformation, die sogenannte Fast FourierTransformation, durch die der Berechungsaufwand der Transformation von O(N^4) auf O(N²logN) abgesenkt wird. Da die Koeffizienten der
aufwändigeren Kosinustransformation aus denen der Fouriertransformation berechnet werden können wird diese in Regel auf die Fast Fourier
Transfomation mit anschließender Berechnung der Koeffizienten zurück geführt.
6.4
Faltungen
Faltungsoperatoren sind eine spezielle Gruppe der linearen Operatoren. Sie sind Verschiebungsinvariant, das bedeutet ihr Einfluss ist
unabhängig vom Ort ihres Einsatzes. Viele Einflüsse der Bildaufnahme sind ebenfalls unabhängig vom Ort und lassen sie deshalb durch einen
solchen Operator beschreiben. Zum Beispiel sind die meisten Rauscheinflüsse Orts unabhängig. Der Einsatz eines Faltungsoperators zur
Beschreibung solcher Einflüsse ist besonders attraktiv auf Grund der Tatsache, dass er selbst dann bestimmt werden kann wenn die Ursache
der Einflüsse unbekannt ist. Neben Linerarität und Verschiebungsinvarianz sind Faltungen assoziativ und kommutativ. Bei der Anwendung
mehrere Faltungen auf ein Bild ermöglicht die Assoziativitätseigenschaft eine effiziente Ausführung. Die unterschiedlichen Operatoren können
zu einem Operator zusammen gefasst werden und auf das Bild angewendet werden. Dies ist ein erheblicher Vorteil, weil mit solchen
Operatoren in der Regel nicht nur Einzelbilder gefiltert, sondern ganze Aufnahmereihen bearbeitet werden sollen.
( g  f )(m, n) 


  g (i, j) * f (i  m, j  n)
i   j  
Berechnung einer Faltung
Wird eine Faltung im Ortsraum ausgeführt, so ist der Aufwand bei einem K*K großen Faltungskern pro Bildpunkt O(K²). Der Gesamtaufwand ist
also O(K²*N²). Durch einige mathematische Umformungen lässt sich für ein und höher dimensionale Funktionen zeigen, dass eine Faltung im
21
Ortsraum einer Multiplikation im Frequenzraum entspricht. Unter Verwendung der Fast Fourierransformation ist der Aufwand für Hin- und
Rücktransformation jeweils O( N 2 log 2 N ) und der Aufwand für die Multiplikation O(N²). Daraus ergibt sich ein Gesamtaufwand
von O( N 2 log 2 N ) . Eine Faltung ist also für log 2 N < K² im Frequenzraum effizienter durchführbar. Da sich die Fouriertransformation
und ihre inverse Transformation nur um ein Vorzeichen unterscheiden, lässt sich umgekehrt beweisen, dass eine Faltung im Frequenzraum
einer Multiplikation im Ortsraum entspricht.
6.5
Korrelationen
Eine Korrelation ist einer Faltung sehr ähnlich, aber unterscheidet sich jedoch in ihrem Anwendungsbereich. Während Faltungen dazu
eingesetzt werden Einflüsse auf das Bild rückgängig zumachen werden Korrelationen dazu genutzt Ähnlichkeiten zwischen Bilder zu
beschreiben. Die Ähnlichkeit zwischen zwei Bildern lässt sich durch ihre Kovarianz beschreiben.
 f ,g 
1
MN
N 1 M 1
  ( f (m, n)  f (m, n))( g (m, n)  g (m, n))
n 0 m 0
Kovarianz zweier Bilder
F und G repräsentieren die Mittelwerte der beiden Abbildungen. Da die Kovarianz sehr stark vom Verhältnis der beiden Varianzen
abhängt ist sie kein perfektes Maß für die Beschreibung der Ähnlichkeit. Es empfiehlt sich eine Normalisierung der Kovarianz mit den beiden
Varianzen der Abbildungen, wodurch sich der sogenannte Korrelationskoeffizient ergibt.
CC f , g 
 f ,g
 2f *  g2
Korrelationskoeffizient
Werte zwischen 0 und 1 bzw. zwischen 0 und -1 geben unterschiedliche Gerade von Streuung der Grauwertkombinationen in der
gemeinsamen Häufigkeitsverteilung an. Der Wert 0 wird angenommen, wenn es keine Ähnlichkeiten zwischen den Bildern gibt und 1 wenn
das eine Bild eindeutig im Anderen wieder gefunden wird. Deshalb können Korrelationen sehr gut für ein Template Matching eingesetzt
werden. Die gesuchte Struktur wird als eine Vorlage implementiert und mit allen Positionen des Bildes korreliert. Anhand der Größe der
errechneten Korrelationskoeffizienten lässt sich die Ähnlichkeit an der Stelle des Bildes mit Vorlage beschreiben. Ein möglichst großer
Korrelationskoeffizient bedeutet hierbei eine möglichst große Übereinstimmung. Allerdings ist diese Berechnung sehr aufwendig, weil für jede
Position der Vorlage die Varianzen und die Kovarianz berechnet werden müssen. Dieser Vorgang lässt sich unter der Annahme, dass der
Mittelwert der Vorlage Null ist und die Vorlage der Größe des Bildes entspricht stark vereinfachen. Dieses Verfahren wird als Kreuzkorrelation
bezeichnet.
22
CC f , g (m, n) 
 f , g (m, n)
1
 2
2
2
 f * g
 f *  g2


M 1 N 1
 ( f (i  m, j  m)  f )(m(i, j)  m )
i 0 j 0
1
 *  g2
M 1 N 1
1
 *  g2
M 1 N 1
2
f
2
f
 ( f (i  m, j  n)  f )m(i, j )
i 0 j 0
 f (i  m, j  n)m(i, j )
i 0 j 0
Überführung der Korrelation in die Kreuzkorrelation
M 1 N 1
( f  g )(m, n)   f (i  m, j  n)m(i, j )
i 0 j 0
Berechnung der Kreuzkorrelation
Da die Kreuzkorrelation der Faltung bis auf das Vorzeichen entspricht gelten die gemachten Aussagen über den Berechnungsaufwand der
Faltung in Orts- und Frequenzraum äquivalent. Eine Faltung entspricht einer Korrelation mit einem um 180° gedrehten Kern.
Bild 35 Korrelation
6.6
Filter
6.6.1
Durchschnittsfilter
Bild 36 Faltung
Der Durchschnittsfilter bewegt seine Filtermaske über das gesamte Bild und berechnet dabei für jede Position der Maske den Durchschnitt
der unterliegenden Pixel neu und ersetzt den Pixel unterhalb der Filtermitte durch diesen[38]. Dadurch werden die Unterschiede zwischen
nahegelegenen Pixel entfernt und das Bild erscheint geglättet. Ein solcher Filter kann zum verwaschen von Kanteninformationen führen[40].
Dies liegt daran, dass ein Durchschnittsfilter meistens als ein rechteckiger gewichteter Faltkern implementiert wird. Eine Filterung entspricht
also einer Faltung im Ortsraum. Da der Rechteckfilter aber im Frequenzraum zu einem Kardinalsinus transformiert [37] verrauschen die
Schwingungsanteile des Kardinalsinus Teile des Bildes.
23
1 / 9 1 / 9 1 / 9
1 / 9 1 / 9 1 / 9


1 / 9 1 / 9 1 / 9
Faltungskern
Bild 37 Transformation eines Rechtfilters in den Frequenzbereich
Bild 38 Anwendung eines 3*3 Durchschnittsfilter
24
Bild 39 Original
6.6.2
Bild 40 Gefiltert
Gaußfilter
G 
1
2 2

e
( x2  y2 )
2 2
Die Gaußglocke ist symmetrisch und gewichtet nahe gelegene Pixel stärker als
weit entfernte. Die Gaußglocke ergibt somit eine kreisförmige nach außen dunkler
werdende Abbildung [42].
Gaußglocke
Bild 41 3D Graph
Bild 42 Abbildung
25
Der Auswirkungen des Gaußfilters können über seine Varianz und die Größe der Filtermaske gesteuert werden. Wird beispielsweise die
Varianz erhöht, so spreizt sich die Glocke auf und es fließen mehr Pixel in die Gewichtung mit ein.
Bild 43 Gaußglocken mit unterschiedlichen Varianzen
Erhöht sich aber die Varianz und verkleinert sich der Kern, dann werden alle Pixel relativ stark gewichtet und der Filter hat kaum eine Wirkung.
Bild 44 Gaußglocken mit unterschiedlichen Kernen
Eine Daumregel besagt, dass die Breite des Kerns mindestens dem dreifachen der Varianz entsprechen sollte. Da die Gaußglocke bei einer
26
Transformation in den Frequenzbereich wieder zu einer Gaußglocke transformiert verrauscht sie im Gegensatz zu anderen Filtern keine
Verrauschung des Signals und ist deshalb die konventionelle Wahl für eine Tiefpassfilterung.
6.6.3
Medianfilter
Im Gegensatz zum Durchschnitts- und Gaußfilter ist der Median ein nicht linearer Filter. Wie schon bei der Erklärung der verschiedenen
Rauscheinflüsse erwähnt eignet sich der Medianfilter sehr gut zum filtern von zufällig verteiltem Rauschen. Sein großer Vorteil gegenüber dem
Durchschnittsfilter ist, dass er die Kanten des Bildes nicht verwischt [38]. Ein Medianfilter muss lediglich einen guten Sortieralgorithmus
implementieren um möglichst effizient zu arbeiten.
Bild 45 Filterverhalten an einer Kanter
27
7
Kanten und Ableitungen
Zunächst wird das Bild partiell Differenziert. Dazu wird das Bild als eine zweidimensionale Funktion mit diskretem Werteberreich und
eingeschränkten Definitionsbereich betrachtet.
Bild 46 Tiger
Bild 47 Ableitung X
Bild 48 Ableitung Y
Der Gradient zeigt dann immer in die Richtung des steilsten Intensitätsanstieges [49].
Bild 49 Gradienten Beispiele verschiedener Intensitätsverläufe
Die Richtung des Gradient bzw. der Kante wird als Phasenverschiebung zwischen den partiellen Ableitungen ausgedrückt.
28
Die Kantenstärke des Bildes ergibt aus der Norm
der partiellen Ableitungen [50].
Bild 50 Kantenstärke
8
Anwendungen im Institut für Lasertechnik
8.1
Geschwindigkeitsmessung mittels Kreuzkorrelation
Bei der Geschwindigkeitsanalyse geht es darum die Bearbeitungsgeschwindigkeit des Prozesses aus den laufenden Aufnahmen der Kamera
zu bestimmen. Über die Aufnahmerate der Kamera und den gemessenen Abstandsinformationen der Bilder kann die
Bearbeitungsgeschwindigkeit errechnet werden. Die Abstände werden mittels einer Kreuzkorrelation gemessen. Damit dieses Verfahren
gleichbleibend gut funktioniert muss dafür gesorgt werden, dass sich die aufgenommenen Bilder während des Prozesses möglichst ähnlich
sind. Mittels Kreuzkorrelation wird nun für einen kleinen Bildausschnitt für jede Position innerhalb eines größeren Bildausschnittes oder dem
Gesamtbild der Korrelationskoeffizient bestimmt. Die Position des größten errechneten Korrelationskoeffizienten kennzeichnet die Lage des
kleinen Bildausschnitts innerhalb des Suchbereiches. Der zurückgelegte Weg des kleinen Bildausschnitts errechnet sich nun als Differenz
seiner Lage im aktuellen Bild zum vorherigen. Da diese Abstände natürlich in Pixeln gemessen werden muss zusätzlich noch der
Vergrößerungsmaßstab des Aufnahmesystems bekannt sein um den reell zurück gelegten Weg bestimmten zu können.
8.2
Nahtfolgeerkennung mittels Konturerkennung
Bei der Nahtfolgeerkennung geht es darum den Bearbeitungspunkt des Lasers zentriert zur Naht auszurichten und ihn während des gesamten
Prozesses in dieser Position zu führen. Auf Grund von thermischen Effekten des Strahlenführungssystems oder Schwingungen des
Bearbeitungskopfes der Anlage kann der Spot des Lasers während des Prozesses von der Naht abwandern. Um einen solchen
unerwünschten Effekt regulieren zu können ist es nötig den aktuellen Abstand zwischen Laserspot und Naht genau zu messen. Hierzu werden
die Bilder des Beobachtungssystems zunächst nach den Reflektionen der Blechkanten segmentiert um die Region der Naht zu erhalten. Nun
wird das Originalbild erneut segmentiert um die Region des Laserspots zu erhalten und die Schwerpunkte beider Regionen berechnet. Der
Abstand des Laserspots zur Naht entspricht dem Abstand der Schwerpunkte beider Regionen. Da dieser Abstand jedoch in Pixeln gemessen
wird ist es nötig den Vergrößerungsmaßstab des Aufnahmesystems zu kennen um den reellen Abstand berechnen zu können. Da es möglich
ist Optiken mit einer gewünschten Vergrößerung zu fertigen können so prinzipiell beliebig kleine Abstände sauber erfasst werden. Ein
29
größeres Problem zur Entwicklung eines zuverlässigen Verfahrens stellt jedoch das unterschiedliche Reflektionsverhalten der verschiedenen
Bearbeitungsmaterialien dar. Da jedes Metall das Licht anders reflektiert kann nicht mit einem manuell festgelegten Schwellwert gearbeitet
werden, sondern es muss für jedes Material ein neuer Schwellwert berechnet werden. Dieser Schwellwert passt sich so an die aktuellen
Reflektionseigenschaften des Materials an. Außerdem ist es wichtig gleichbleibende Reflektionen entlang der Blechkanten zu garantieren,
damit die Region der Naht sauber erfasst werden kann. Hierzu müssen zusätzliche Fremdbeleuchtungen, die in einem festen Winkeln zur Naht
stehen und somit eine gleichbleibende Beleuchtungssituation garantieren eingesetzt werden.
8.3
Referenzfilmvergleich mittels Kreuzkorrelation
Beim Referenzfilmvergleich geht es darum die Qualität bzw. den Zustand eines beobachteten Prozess durch Vergleich mit einem möglichst
idealen Referenzfilm zu beurteilen. Ein solcher Referenzfilm muss zunächst experimentell aus einer Versuchreihe bestimmt werden. Ziel der
Versuchreihe ist es den Prozess in Bezug auf das gewünschte Ergebnis des Vergleiches möglichst gut abzubilden. Ideal wäre es, wenn die
Einzelbilder des Referenzfilmes Mittelwerte von beispielweise zehn guten Bildern der Versuchreihe wären, damit kleine Fluktuationen der
Aufnahme nicht so stark ins Beurteilungsergebnis mit einfließen. Nach der Erstellung eines geeigneten Referenzfilm kann mit seiner Hilfe ein
Prozess analysiert werden. Hierzu wird für jedes Bild des Prozess der Korrelationskoeffizient mit dem entsprechenden Bild des Referenzfilms
berechnet. Anhand der Größe des Koeffizienten wird die Übereinstimmung des Prozesses mit dem Film beurteilt. Damit sich der Referenzfilm
auch für den gleichen Prozess bei anderer Ortsauflösung eignet, empfiehlt es sich den Referenzfilm in einem skalierbaren Format zu
speichern. Dadurch wird verhindert, dass für jede mögliche Ortsauflösung ein eigener Referenzfilm erstellt werden muss.
8.4
Zählungen von Pulververteilungen
Bei diesem Prozess geht es darum möglichst gleiche Pulvermengen durch kreisförmig angeordnete Düsen in die Prozesszone einzubringen.
Hierzu werden die Häufigkeitsverteilungen von ausgestoßen Pulverteilchen am Ausgang jeder Düse erfasst und verglichen. Zur Zählung der
Pulverteilchen wird das Bild in N Dreiecke zentriert zu den N Düsen zerlegt. Anschließend wird das Bild nach den Helligkeiten der
Pulverteilchen segmentiert und diese mittels Region Labbelling abgezählt. Die Menge der Teilchen unter einem bestimmten Dreieck
entspricht der Anzahl von dieser Düse eingebrachten Pulvermenge. Da diese in der Regel relativ hoch ist kann die Häufigkeitsverteilung der
Düse über eine Gaußverteilung genährt werden. Anhand der Varianzen und Mittelwerte der unterschiedlichen Verteilungen an den Düsen lässt
sich die Gleichmäßigkeit der eingebrachten Pulvermenge einfach kontrollieren.
8.5
Intensitätsverteilungen beim Laserbohren
Laserbohren ist ein sehr schnelles und sauberes Bohrverfahren. Zur Prüfung ob ein Laser eine Bohrung erfolgreich abgeschlossen hat wird
von der Annahme ausgegangen, dass solange sich noch Materialrückstände im Bohrloch befinden große Anteile der Laserstrahlung zurück
reflektiert werden. Diese reflektierte Strahlung wird während der Bohrung über eine Kamera aufgezeichnet. Die Wellenlänge des
Bearbeitungslasers sollte dazu wenn möglich oberhalb des Empfindlichkeitsbereiches der Kamera liegen, weil dann die reflektierte
Laserstrahlung in jedem Fall als weiße Pixel im oberen Intensitätsbereich abgebildet wird. Dieser Effekt kann natürlich auch in umgekehrter
Weise ausgenutzt werden. Nun werden die prozentualen Histogramme der Bilder betrachtet und geguckt ob der Anteil des oberen
Intensitätsbereiches unter eine experimentell festgestellte Schranke abfällt. In einem solchen Fall ist kein Material mehr im Bohrloch zu finden
30
und es kann davon ausgegangen werden das der Laser das Material vollständig durchbrochen hat. Es ist nötig die prozentuale Schrank
zunächst experimentell zu bestimmten, weil sie natürlich stark von der restlichen Beleuchtungssituation der Anlage abhängt. Die Schranke
prozentual anstatt absolut zu messen hat den Vorteil, dass sie auf Aufnahmen verschiedener Auflösungen gleichbleibend gut angewendet
werden kann, sofern sich die Beleuchtungssituation durch die höhere Auflösung nicht verändern.
9
Zusammenfassung
In dieser Seminararbeit werden Algorithmen zur Bearbeitung von monochromen Bildern vorgestellt und einige Anwendungen aus dem Bereich
der Lasertechnik präsentiert. Die Arbeitsweise eines optischen Aufnahmesystems wird am Beispiel eines Halbleiter Bildsensors erklärt und
diverse Störeinflüsse vorgestellt. Außerdem wird die Funktionsweise und Effizienz von transformierten Darstellungen im Frequenzraum
ausführlich erläutert und kurz auf die Bedeutung von Ableitungen für die Kantererkennung eingegangen.
Literaturverzeichnis
Links
http://de.wikipedia.org/wiki/Schwellwertverfahren
http://en.wikipedia.org/wiki/Thresholding_%28image_processing%29
Präsentationen & Papers
Prof. Dr. Bastian Leibe, Computer Vision, Aachen 2008
Bücher
Klaus D. Tönnies: Grundlagen der Bildverarbeitung, Pearson Studium, Berlin 2005, ISBN 3-8273-7155-4
Bernd Jähne: Digitale Bildverarbeitung. 6., überarbeitete und erweiterte Auflage. Springer, Berlin 2002, ISBN 3-540-24999-0
31
Gary Bradski & Adrian Kaehler: Learning OpenCV: Computer Vision with the OpenCV Libary, O’Reilly , 2008, ISBN 978-0-596-51613-0
Rafael C. Gonzales, Richard E. Woods: Digital Image Processing. Prentice Hall, New Jersey 2002, ISBN 0-201-18075-8
32