Programmierpraktikum Einführung in die
Werbung

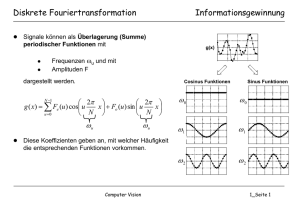
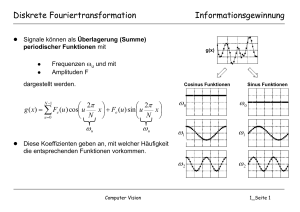
Technische Universitat Munchen Institut für Informatik Lehrstuhl Informatik IX Prof. Dr. Bernd Radig SS 05 15. Juni 2005 Aufgabenblatt 8 Programmierpraktikum Einführung in die Bildverarbeitung Achtung: Die Bearbeitungszeit für dieses Blatt beträgt 2 Wochen, Abgabetermin ist folglich der 6. Juli 2005. Technische Universität München Institut für Informatik Lehrstuhl Informatik IX Prof. Dr. Bernd Radig SS 05 22. Juni 2005 Aufgabenblatt 8 Programmierpraktikum Einführung in die Bildverarbeitung Auf diesem Blatt behandeln wir die Filterung im Frequenzraum. Wir haben bereits einige Filter im Ortsraum kennengelernt, welche wir durch die Faltungsoperation implementiert haben (siehe Aufgabenblatt 5). Diese haben allerdings den Nachteil, daß sie bei grossen Bildern und Filterkernen relativ langsam laufen und, daß sie z.B. bei Tiefpassoperationen keine Information darüber geben, bis zur welche Frequenzen gefiltert werden. Diese Nachteile kann man umgehen, wenn man die entsprechende Filterung im Frequenzraum durchführt. Die Faltung im Ortsraum entspricht der Multiplikation im Frequenzraum. D.h. Eine entsprechende Filterung erhält man, wenn man Bild und Filterkern in den Frequenzraum transformiert, dort komponenetenweise miteinander multipliziert und das Resultat in den Ortraum wieder zurücktransformiert. Glücklicherweise ist man nicht gezwungen den Filterkern zu transformiren, sondern kann im Frequenzraum einfachere und effektivere Filtermasken erstellen, so daß sich der Aufwand auf die Transformation, inverse Transformation und einer komponentenweise Multiplikation reduziert. Die Transformation des Bildes in den Frequenzraum erfolgt durch die diskrete Fourier-Transformation (DFT) entsprechend ist die inverse Transformation (also vom Frequenzraum in den Bildraum/Ortsraum) die inverse DFT (IDFT). Sei B(x) die Bildfunktion im Ortsraum; die 1 dimensionale diskrete Fouriertransformation ist wie folgt definiert: N −1 n·u F (u) = B(n) · ei·−2π N n=0 wie man hier deutlich sehen kann, ist ei·−2π und kann somit umgeformt werden zu: N −1 n·u N die Eulerdarsellung einer komplexen Zahl N −1 n·u n·u n·u n·u ) + i · sin(−2π )) = ) − i · sin(2π )) F (u) = B(n) · (cos(−2π B(n) · (cos(2π N N N N n=0 n=0 Entsprechend ist die 1 dimensionale inverse diskrete Fouriertransformation (IDFT) gegeben durch: B(x) = N −1 N −1 n·x 1 n·x 1 n·x · · ) + i · sin(2π )) F (n) · ei·2π N = F (n) · (cos(2π N n=0 N n=0 N N Die 2 dimensionale DFT F (u, v) kann durch 2 aufeinanderfolgende 1 dimensionale DFT’s berechnet werden. Zuerts werden die Zeilen transformiert und das Ergebnis als Complexe Werte in einem Array gespeichert (Realteil und Imaginärteil). Danach werden die Spalten des neu gewonnenen Arrays transformiert und man erhält die 2D-DFT des Ursprungbildes. Bei der ersten DFT sind die Werte von B(x) (Zeile) reel, bei der zweiten DFT sind diese Werte complex und müssen in der Berechnung des Produktes (innerhalb der Summe) entsprechend richtig multipliziert werden! Entsprechend funktioniert die 2D-IDFT: zuerst berechnet man die IDFT der Spalten; dann die IDFT über die Zeilen des Resultats (und erhält hoffentlich das richtige Ergebnis). Filtern im Frequenzraum: Wie bereits oben erwäht erfolgt eine Filterung im Frequenzraum durch komponentenweise Multiplikation der Fourieretransformierten F (u, v) und der Filtermaske H(u, v). Üblicherweise liegen die Werte der Filtermaske zwischen 0 und 1, und die Maske hat die selben Ausmaße wie die Fouriertransformierte. Aufgaben 1. Erstellen Sie die Klasse FourierImage, abgeleitet von DataObject. Diese kapselt das Ergebnis einer Fouriertransformation, also eine zweidimensionale Matrix mit Elementen aus C, deren Grösse der des Urbildes entspricht (also gleichviele Spalten/Zeilen besitzt). Wählen Sie hierfür eine effiziente Darstellung1 ! Die Klasse FourierImage existiert somit parallel zur Klasse Image. Die Umwandlung von Image nach FourierImage wird durch den Operator Fourier vorgenommen, die einen Eingabeport vom Typ Image und einen Ausgabeport vom Type FourierImage besitzt. Die Rückwandlung wird von InverseFourier durchgeführt. Filter im Frequenzraum haben FourierImage sowohl als Eingabe, als auch als Ausgabe. 2. Erstellen Sie die Klasse FourierImageViewerPanel, auf dem ein Fourierbild angezeigt werden kann. Eine Instanz dieses Panels wird von der Methode getViewPanel() der Klasse FourierImage zurückgegeben. Die Elemente des Fourierbildes F (u, v) = a + bi sind komplexe Zahlen, und können somit nicht unmittelbar dargestellt werden. Auf dem Panel soll daher wahlweise das Powerspektrum oder das Phasenbild des Fourierbildes zu sehen sein. Beachten Sie folgendes: • Das Powerspektrum √ zeigt für jeden Bildpunkt den Betrag des zugeordneten Elements an, also a2 + b2 . Damit das Powerspektrum besser sichtbar wird, muss dieser Wert logarithmisch skaliert werden: c · ln(1 + √ a2 + b2 ) Die Konstante c ist dabei vom Bild abhängig us muss so gewählt werden, dass der zur Verfügung stehende Bereich von 0 bis 255 optimal ausgenutzt wird. 1 Eine Darstellung wie z.B. Complex[][], wobei Complex ein selbst definierter Datentyp zur Repräsentation komplexer Zahlen wäre, ist nicht effizient, also denken Sie sich etwas anderes aus :-) • Zur intuitiveren Darstellung des Powerspektrums sollen beim Anzeigen die Quadranten des Bildes vertauscht werden: 2 1 4 3 3 4 1 2 • Das Phasenbild zeigt den der komplexen Zahl a + bi zugeordneten Winkel φ an, d.h. den Winkel, den der Vektor (a, b)T mit der x-Achse bildet. Dieser Winkel liegt im Intervall [0; 2π[ und muss zur Anzeige auf den Bereich von 0 bis 255 abgebildet werden. 3. Erstellen Sie den Operator FourierTransform, welcher als Eingabe ein Grauwert-Bild erwartet und als Ausgabe die 2D-Fouriertrandformierte des Bildes zurückgibt. 4. Erstellen Sie den Operator InverseFourierTransform, welcher als Eingabe ein FourierImage erwartet und als Ausgabe die inverse Fourier-transformierte (Grauwert-Bild) zurückgibt. 5. Erstellen Sie den Operator FreqFilter, welcher eine Vielzahl von Filtern im Frequenzraum anbietet. Der Operator erwartet als Eingabe ein FourierImage und gibt als Ausgabe wiederum ein FourierImage zurück. Die Filterung erfolgt durch Erstellen einer Filtermaske H(u, v) und Anwenden dieser Filtermaske auf die Fouriertransformierte F (u, v). Vorsicht: Die Filtermasken sind hier so definiert, daß die Quadranten wie bei dem Powerspektrum vertauscht sind und der Ursprung in der Mitte angenommen wird: Richtig umrechnen! Dieser Operator hat die beiden integer-Parameter param1 und param2 und einen enum Parameter mit folgenden Einträgen: Tiefpass: Filtert die FourierTransformierte mit einer Filtermaske, welche wie folgt definiert ist: 1 falls x2 + y 2 < param12 H(u, v) = 0 sonst Hochpass: Filtert die FourierTransformierte mit einer Filtermaske, welche wie folgt definiert ist: 1 falls u2 + v 2 > param12 H(u, v) = 0 sonst Bandpass: Filtert die FourierTransformierte mit einer Filtermaske, welche wie folgt definiert ist: 1 falls u2 + v 2 > param12 ∧ u2 + v 2 < param22 H(u, v) = 0 sonst Richtung: Dieser Filter erzeugt eine Filtermaske entsprechend der Abbildung: param1 param2 param1 und param2 sind in Grad angegeben und entsprechen dem Winkel in welcher der Doppelkegel liegt bzw. dem Öffnungswinkel des Doppelkegels. BWTief: Filtert die FourierTransformierte mit einer Filtermaske, welche wie folgt definiert ist: 1 falls √ 2 12 2·param2 u +v 1+ param1 H(u, v) = 0 sonst Dieser Filter ist der Butterworth-Tiefpass-Filter. (weitere Infos kann man zu genüge im Internet finden.) BWHoch: Filtert die FourierTransformierte mit einer Filtermaske, welche wie folgt definiert ist: 1 2·param2 1 falls param1 1+ √ 2 2 H(u, v) = u +v 0 sonst Dieser Filter ist der Butterworth-Hochpass-Filter. (weitere Infos kann man zu genüge im Internet finden.) 6. Zusatzaufgabe: Die DFT hat eine Zeitkomplexität von O(n4 ). Es gibt eine schnellere Variante, die diese Transformation in O(n2 ·log(n)) erledigt; die Schnelle Fourier Transformation (Fast Fourier Transform: FFT). Die Implementierung der DFT wie sie oben beschrieben ist, ist pflicht! Wer aber darüberhinaus Lust und Zeit hat, kann zusätzlich die FFT implementieren, oder eine bereits vorhandene Implementierung (wie sie zu genüge im Internet zu finden sind) verwenden, und die Operatoren erweitern, daß die FFT auch zur Auswahl steht. Der Geschwindigkeitvorteil ist enorm gengeüber der DFT. Viel Spaß!