diskrete Fouriertransformation (DFT) - home.hs

Diskrete Fouriertransformation
Informationsgewinnung
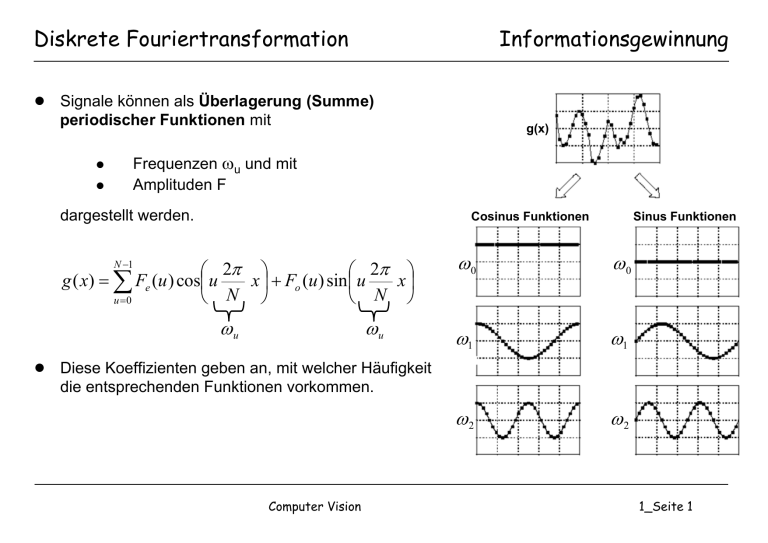
● Signale können als Überlagerung (Summe)
periodischer Funktionen mit
z
z
g(x)
Frequenzen ωu und mit
Amplituden F
dargestellt werden.
Cosinus Funktionen
⎛ 2π ⎞
⎛ 2π ⎞
g ( x) = ∑ Fe (u ) cos⎜ u
x ⎟ + Fo (u ) sin ⎜ u
x⎟
⎝ N ⎠
⎝ N ⎠
u =0
N −1
ωu
ωu
Sinus Funktionen
ω0
ω0
ω1
ω1
ω2
ω2
● Diese Koeffizienten geben an, mit welcher Häufigkeit
die entsprechenden Funktionen vorkommen.
Computer Vision
1_Seite 1
Diskrete Fouriertransformation
Informationsgewinnung
● Die Berechnung der Koeffizienten heißt diskrete Fouriertransformation (DFT) und erfolgt via
N −1
⎛ ux ⎞
g
x
(
)
cos
⎜ 2π ⎟
∑
N⎠
⎝
x =0
1 N −1
⎛ ux ⎞
Fo (u ) = − ∑ g ( x) sin ⎜ 2π ⎟
N x =0
N⎠
⎝
1
Fe (u ) =
N
● Aus den Koeffizienten kann das Originalsignal zurück gewonnen werden: Inverse diskrete
Fouriertransformation (IDFT)
N −1
⎛ ux ⎞
⎛ ux ⎞
g ( x) = ∑ Fe (u ) cos⎜ 2π
⎟ + Fo (u ) sin ⎜ 2π
⎟
N ⎠
N ⎠
⎝
⎝
u =0
Computer Vision
1_Seite 2
Diskrete Fouriertransformation
Informationsgewinnung
● Die Fouriertransformation und ihre Inverse werden oft in komplexer Schreibweise1)
angegeben:
DFT:
IDFT:
N −1
1
F (u ) =
N
∑ g ( x )e
−i 2π
1
g ( x) =
N
N −1
i 2π
ux
N
0≤u< N
x =0
∑ F (u )e
ux
N
0≤ x< N
u =0
F(u)
Fo(u)
F (u ) = Fe (u ) + Fo (u )
2
⎛ Fo (u ) ⎞
⎟⎟
φ (u ) = arctan⎜⎜
⎝ Fe (u ) ⎠
2
|F
(u
)|
● Es ist
φ (u )
Amplitude (Magnitude)
Fe(u)
Phase
1) Die Umrechung von reeller in komplexe Schreibweise erfolgt mit
Computer Vision
eiϕ = cos(ϕ ) + i sin(ϕ )
1_Seite 3
Diskrete Fouriertransformation
Informationsgewinnung
● Die Fouriertransformation und ihre Inverse bilden einen Zusammenhang zwischen Orts- und
Frequenzraum
Ortsraum
Frequenzraum (Amplitude)
F (u )
g (x)
x
u
Frequenz
Notation:
F
g
oder
F{g} oder ĝ
Zweidimensional?
Computer Vision
1_Seite 4
Diskrete Fouriertransformation
Informationsgewinnung
Die zweidimensionale diskrete Fouriertransformation und ihre Inverse. Bild g ( B x H )
● DFT:
F (u , v) =
1
B⋅H
B −1 H −1
∑∑ g ( x, y) ⋅ e
− 2πi (
ux vy
+ )
B H
0≤u< B 0≤v< H
x =0 y =0
Ortsraum g ( x, y )
Frequenzraum
u
x
v
y
● Die Inverse: IDFT
g ( x, y ) =
1
B⋅H
B −1 H −1
∑∑ F (u, v) ⋅ e
2πi (
ux vy
+ )
B H
Re( F{g})
u
v
Im(F{g})
0≤ x< B 0≤ y<H
u =0 v =0
Computer Vision
1_Seite 5
Diskrete Fouriertransformation
Darstellung im Frequenzraum
Informationsgewinnung
F (u , v) = Re( F (u , v)) 2 + Im(F (u , v)) 2 Amplitude
⎛ Im(F (u, v)) ⎞
⎟⎟
⎝ Re( F (u , v)) ⎠
φ (u , v) = arctan⎜⎜
Frequenzraum (Amplitude und Phase)
Frequenzraum
u
u
bzw.
v
Re( F {g})
Phase
v
u
v
F
Bemerkung:
Wegen der Punktsymmetrie
muss nur eine Hälfte der DFT
berechnet werden und der
Ursprung kann in den
Bildmittelpunkt gelegt werden:
u
u
u
bzw.
A
bzw.
D
B
v
Im(F{g})
v
φ
Computer Vision
B
A
v
1_Seite 6
Diskrete Fouriertransformation
Amplitude
Informationsgewinnung
Phasen
Amplitude
Die Phase beinhaltet entscheidende Informationen!
Quelle: Jähne B. Digitale Bildverarbeitung
Computer Vision
1_Seite 7
Diskrete Fouriertransformation
Informationsgewinnung
Im Frequenzraum sind viele Operationen günstiger durchzuführen:
● Alle linearen Operationen z.B. Hochpass, Tiefpass und Bandpass können mit hoher Güte
durchgeführt werden. Der Faltungssatz besagt u.a., dass eine Faltung im Ortsbereich auch
durch eine Multiplikation im Frequenzbereich durchgeführt werden kann:
1)
F {g ⊗ f } = F {g }⋅ F { f }
F {g ⋅ f } = F {g }⊗ F { f }
● Erkennung periodischer Strukturen
● Manipulation periodischer Strukturen
Manipulation von
F im
g
1) Multiplikation von komplexen Zahlen:
F
Frequenzraum
F'
( x + iy ) ⋅ ( x'+iy ' ) = ( xx'− yy ' ) + i ( xy '+ x' y )
Computer Vision
g'
1_Seite 8
Diskrete Fouriertransformation
Beispiel: Tiefpaßfilter durch
g~ = G ⊗ g
Informationsgewinnung
mit G ( x, y ) =
−
1
2πσ 2
e
x2 + y2
2σ 2
● Erinnerung: separierbarer Kern
⎡0.0625⎤
⎢ 0.25 ⎥
⎢
⎥
[0.0625 0.25 0.375 0.25 0.0625]⊗ ⎢ 0.375 ⎥
⎢
⎥
0
.
25
⎢
⎥
⎢⎣ 0.065 ⎥⎦
σ 2 ≈ 1.14
● Anwendung des Faltungssatzes (Führe anstelle der Faltung im Ortsraum eine Multiplikation
im Frequenzraum durch):
F {G ⊗ g } = F {G}⋅ F {g }
Computer Vision
1_Seite 9
Diskrete Fouriertransformation
Informationsgewinnung
● Koordinatensysteme von Bild und Kern: F {G ⊗ g } = F {G}⋅ F {g }
G ( x, y ) =
x
−
1
2πσ 2
e
x2 + y2
2σ 2
σ 2 ≈ 1.14
x
x
y
y
y
g ( x, y )
D
B
A
A
B
Für die DFT muss der Ursprung des Kerns dem Ursprung des Bildes entsprechen!
Computer Vision
1_Seite 10
Diskrete Fouriertransformation
Ortsraum
Informationsgewinnung
Frequenzraum
DFT
Ortsraum
Re( F {g})
g
Im(F{g})
Re( F {G} ⋅ F{g})
IDFT
G⊗g
DFT
Re( F {G})
Im(F{G} ⋅ F{g})
G
Im(F{G})
Multiplikation von komplexen Zahlen:
( x + iy ) ⋅ ( x'+iy ' ) = ( xx'− yy ' ) + i ( xy '+ x' y )
Computer Vision
1_Seite 11
Diskrete Fouriertransformation
Informationsgewinnung
● Die Berechnung des Kerns für die Gaußfunktion muss nicht durchgeführt werden, da die
Gaußfunktion im Frequenzbereich wieder eine Gaußfunktion (mit reziproker Varianz) ist:
−
1
2πσ
2
e
x2 + y2
2σ
1
2
2πσ 2
−
e
u 2 +v2
2σ '2
mit σ '2 =
1
(2πσ ) 2
● Die Fouriertransformierte lässt sich für weitere Funktionen analytisch berechnen, z. B.
Quelle: Handbook of Computer Vision
Computer Vision
1_Seite 12
Diskrete Fouriertransformation
Informationsgewinnung
Eigenschaften der DFT
Quelle: Handbook of Computer Vision
Computer Vision
1_Seite 13
Diskrete Fouriertransformation
Informationsgewinnung
Effizienz:
Beispiel: N:=B=H, dann hat die Berechnung der DFT einen Aufwand von O(N4)
void DFT(const CImageMemory< unsigned char >& source,
CImageMemory< unsigned char >& real, CImageMemory< unsigned char >& imag)
{
... Parametervereinbarung ...
for (v = 0; v < H; v++)
wird für alle v und y
wird für alle u und x
{
berechnet
berechnet
for (u = 0; u < B/2; u++)
{
realTeil = 0; imagTeil = 0;
for (y = 0; y < H; y++)
{
for (x = 0; x < B; x++)
{
summand = - fac * ((u*x)/double(B) + (v*y)/double(H));
realTeil += source.GetPixelValue(x,y) * cos(summand);
imagTeil += source.GetPixelValue(x,y) * sin(summand);
}
}
real.SetPixelValue(u,v,realTeil/sqrt_B_H);
imag.SetPixelValue(u,v,imagTeil/sqrt_B_H);
}
}
}
= F (u , v)
Computer Vision
1_Seite 14
Diskrete Fouriertransformation
Informationsgewinnung
● Effizienz: Die DFT kann separiert werden:
vy
ux
− 2πi ( ) ⎞ − 2πi ( )
1 B −1 ⎛ H −1
H ⎟
B
⎜ ∑ g ( x, y ) ⋅ e
F (u, v) =
e
∑
⎟
B ⋅ H x =0 ⎜⎝ y =0
⎠
0≤u< B 0≤v< H
Eindimensionale DFT (abh. von x und v, unabh. von u) !
x
x
1-dim DFT
1-dim DFT
y
u
v
v
● Weitere Effizienzsteigerung: Für die DFT existieren effiziente Verfahren, z.B. die FFT (Fast
Fourier Transformation): DFT Implementierung nach dem Teile und Herrsche Prinzip.
Voraussetzung: Die Bildhöhe und –breite sind Zweierpotenzen, also
B = 2k
und
H = 2l
Computer Vision
für l , k = 1,2,...
1_Seite 15
Diskrete Fouriertransformation
Informationsgewinnung
● Beispiel: Faltung von Gaußfunktion und Grauwertkeil durch Multiplikation im Frequenzraum
Ortsraum
Ortsraum
komplexe
Multiplikation
DFT
IDFT
g
DFT
≠ G ⊗ g !!!!
G
Die Fouriertransformation geht von periodischen Signalen aus!!!
Computer Vision
1_Seite 16
Diskrete Fouriertransformation
Informationsgewinnung
Typische Randeffekte nichtperiodischer Signale
Frequenzraum
(Amplitude)
Ortsraum
Abhilfe: Multiplikation im Ortsbereich mit einer Fensterfunktion
Computer Vision
1_Seite 17
Diskrete Fouriertransformation
Informationsgewinnung
Eigenschaften der Fouriertransformation 1: Bezeichungen gˆ = F {g}, fˆ = F { f }
● Linearität (a,b reelle Zahlen)
a g ( x, y ) + b f ( x, y )
a gˆ (u , v) + b fˆ (u , v)
a g ( x, y )
a gˆ (u , v)
insbesondere ist
Beispiel: Bild g(x,y) invertieren: f(x,y) := 255
● Verschiebung im Ortsbereich
f ( x, y ) − g ( x, y )
fˆ (u , v) − gˆ (u , v)
g ( x − x0 , y − y0 )
e −2πi ( ux0 +uy0 ) gˆ (u , v)
● Verschiebungen im Frequenzbereich
e 2πi ( u0 x +u0 y ) g ( x, y )
Computer Vision
gˆ (u − u0 , v − v0 )
1_Seite 18
Diskrete Fouriertransformation
Informationsgewinnung
Eigenschaften der Fouriertransformation 2:
● Ähnlichkeit (invertierbare 2x2 Matrix A)
insbesondere ist für Drehungen U
g ( A( x, y ))
1
gˆ (( A−1 )T (u , v))
det( A)
g (U ( x, y ))
gˆ (U (u , v))
Frequenzraum (Amplitude)
Ortsraum
90°Drehung
nach rechts
90°Drehung
nach rechts
Computer Vision
1_Seite 19
Diskrete Fouriertransformation
Informationsgewinnung
Frage: Wie stark kann ein Bild ohne Informationsverlust in der Größe reduziert werden?
jeder 4. Bildpunkt
in x-und yRichtung
Δx = Δy = 4
jeder 5. Bildpunkt
in x-und yRichtung
Δx = Δy = 5
Moiré-Effekt:
Das Abtasttheorem wurde verletzt!
Pro Wellenlänge werden mindestens zwei Abtastpunkte benötigt!
Quelle: Jähne B. Digitale Bildverarbeitung
Computer Vision
1_Seite 20
Diskrete Fouriertransformation
Informationsgewinnung
Abtastungen:
● Bestimme die oberen Grenzfrequenzen im Bildbereich: gˆ (u, v) = 0 ∀ u > u0 , ∀ v > v0
u
v
● Normierung bzgl. Bildbreite und -höhe u~ = 0 v~ = 0
B
H
Abtasttheorem: Gilt Δx <
1
1
und
, so kann das Bild aus den
Δ
y
<
~
~
2 ⋅u
2 ⋅v
abgetasteten Punkten exakt rekonstruiert werden.
Ortsraum
Frequenzraum (Amplitude)
u
v
u0 ≈ 24.5
Quelle: Jähne B. Digitale Bildverarbeitung
Computer Vision
u~ ≈ 0.196 ⇒ Δx < 2.55
1_Seite 21
Diskrete Fouriertransformation
Informationsgewinnung
Zusammenfassung:
● Die DFT geht von periodischen Signalen aus.
● Die DFT liefert das Spektrum eines Bildes.
● Die DFT transformiert ein Bild in zwei Bilder mit identischer Größe (Real- und Imaginärteil).
Diese können in Phase und Amplitude umgerechnet werden.
● Faltungssatz: Faltungen im Ortsbereich können als Multiplikation im Frequenzbereich
durchgeführt werden.
● Diverse Funktionen und Operationen können analytisch auf den Frequenzbereich
übertragen werden.
● Das Spektrum liefert Informationen für die verlustfreie Abtastmöglichkeit (Abtasttheorem).
● Die Manipulation des Spektrums (auch in einer einzigen Frequenz) beeinflusst das gesamte
daraus rekonstruierte Bild.
g ( x, y ) =
1
B⋅H
B −1 H −1
∑∑ F (u, v) ⋅ e
2πi (
ux vy
+ )
B H
0≤ x< B 0≤ y< H
u =0 v =0
Computer Vision
1_Seite 22