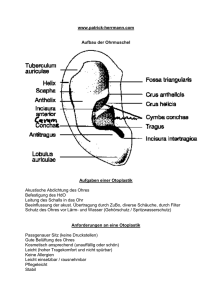
Dokumentieren 2031789
Werbung

Grundlagen 2 Grundlagen 2.1 Thermodynamik von Polymerblends Gemäß der Thermodynamik wird die Mischbarkeit (von Polymeren) durch die Veränderungen bestimmt, denen die freie Enthalpie G infolge einer Durchmischung unterworfen ist. Gmix = Umix + pVmix - TSmix = Hmix - TSmix (1) Die Beiträge der Entropie- Smix und Enthalpieänderungen Hmix lassen sich mit Hilfe verschiedener Theorien[18] berechnen, die sich hinsichtlich ihrer Komplexität, Qualität und Anwendbarkeit unterscheiden. Die erste Theorie geht auf FLORY und HUGGINS (Gittermodell) zurück. Sie zeichnet sich durch ihre Anschaulichkeit und ihre grundlegenden, qualitativ wertvollen Ergebnisse aus. Ein Mangel dieser Theorie besteht darin, daß es nicht möglich ist, aus den Stoffdaten der reinen Komponenten oder über molekulare, strukturelle Beiträge (Vor)Aussagen über den darin definierten Wechselwirkungsparameter ij bzw. zum Mischungsverhalten zu machen. Daher wurden komplexere und auf reinen Stoffdaten basierende Modelle entwickelt: dazu zählen die „Equation of State Theories“ von FLORY, das „Gas-Lattice Model“ von KONINGSVELD, die „Cell-Hole Theory“ von SIMHA, das „Strong Interaction Model“ von ten BRINKE und KARAZS und der „Heat of Mixing Approach“ von PAUL. Sie sind der FLORYHUGGINS-Theorie insofern überlegen, daß sie deutlich machen, welche Parameter in ihrer Einflußnahme auf das Mischungsverhalten von Bedeutung sind. Ihre Anwendbarkeit ist jedoch (zur Zeit noch) auf Ausnahmen beschränkt, weil die erforderlichen thermodynamischen Stoffdaten (isobarer thermischer Ausdehnungskoeffizient, isothermer Kompressibilitäts- bzw. Druckkoeffizient, ...) nur in den wenigsten Fällen experimentell bestimmt sind, die Berechnung von Phasengleichgewichten, Binodalen und Spinodalen mit großem mathematischen und zeitlichen Aufwand verbunden und die Übereinstimmung zwischen Theorie und Experiment trotz des größeren Aufwandes nur bedingt quantitativ ist. Daher wird die FLORY-HUGGINS-Theorie in der aktuellen Literatur (häufig) wie auch in der vorliegenden Arbeit als Grundlage zur Beschreibung von Polymerblends herangezogen. 5 Grundlagen 2.1.1 FLORY-HUGGINS-Theorie[19] Die FLORY-HUGGINS-Theorie ist ursprünglich[20] für Polymerlösungen entwickelt worden, später jedoch von SCOTT und TOMPA[21] auf lösungsmittelfreie Systeme übertragen worden. Es wird angenommen, daß Lösungsmittelmoleküle bzw. die Grundeinheiten der Polymerketten auf eine Art Gitter plaziert werden können. Aus der gegenseitigen Anordnung der Grundeinheiten bzw. der Lösungsmittelmoleküle kann dann die Entropieänderung, aus den auftretenden Wechselwirkungen die Enthalpieänderung berechnet werden. Eine Kompressibilität der Mischungen wird nicht berücksichtigt. Es resultiert die FLORY-HUGGINSGleichung (i = 1 für alle Komponenten) für binäre Systeme G mix RT 1 ln 1 2 ln 2 1212 P2 P1 (2a) bzw. ternäre Systeme G mix RT 1 ln 1 2 ln 2 3 ln 3 1212 1313 2323 P2 P3 P1 (2b), wobei R die allgemeine Gaskonstante, T die absolute Temperatur, i der Volumenanteil, Pi der Polymerisationsgrad des Polymeren i (bei Lösungsmitteln ist P = 1) und ij der FLORYHUGGINS-Wechselwirkungsparameter zwischen den Komponenten i und j ist. Die Terme i/Pilni beschreiben die kombinatorische Mischungsentropie, die Terme ijij die Mischungsenthalpie, wobei ij rein enthalpischer Natur und der Temperatur reziprok proportional sein sollte. Experimentelle Untersuchungen haben jedoch gezeigt, daß ij auch von i, Pi, p oder in komplexerer Form von T abhängen kann. Damit wird auch das an unterschiedlichen Systemen beobachtete LCST-, LCST-UCST, closed loop- oder Uhrglas-Verhalten erklärbar, während die restriktive Bedingung ij = konst./T ausschließlich ein UCST-Verhalten zuläßt. Die bestehende FLORY-HUGGINS-Theorie ist schließlich in der Form erweitert worden, daß alle Abweichungen, die durch (die aufgezeigten) Mängel zustande kommen, im FLORYHUGGINS-Wechselwirkungsparameter ij berücksichtigt werden, d.h. daß ij die Form einer mathematischen Funktion annimmt: ij f i , T, p, Pi . Auf diese Weise lassen sich alle Systeme quantitativ erfassen bzw. können mathematisch angepaßt werden, ohne daß die einfache Struktur der Gleichungen (2a) bzw. (2b) verlorengeht. 6 Verschiedene Formen von Phasendiagrammen Grundlagen Aus der FLORY-HUGGINS-Gleichung geht hervor, daß mit steigendem Polymerisationsgrad Pi der (stets negative) Entropieterm immer mehr an Bedeutung verliert. Bei zwei in gleichen Anteilen ( 1 2 0,5 ) vorliegenden Polymeren mit P1 P2 1000 beträgt die Mischungsentropie bei 20°C nur - 1,69J/mol , und 12 darf keine größeren Werte als 0,00277 annehmen, wenn G mix 0 ( Mischbarkeit) sein soll. Mischungen niedermolekularer Substanzen mit P = 1 können Wechselwirkungsparameter bis zu 2,77 aufweisen, ohne sich zu entmischen, da die Mischungsentropie - 1690J/mol bei 20°C beträgt. Die (enthalpischen) Wechselwirkungen von Polymeren und den niedermolekularen Analogen sind dagegen vergleichbar groß und wenn keine spezifischen Wechselwirkungen (Dipol-Dipol, Charge-Transfer, Salzbildung, Wasserstoffbrückenbindungen) vorliegen - positiv. Die Mischbarkeit vieler (niedermolekularer) Systeme wird somit durch einen großen Entropiegewinn, weniger durch günstige enthalpische Wechselwirkungen verursacht. Die wichtigsten Ergebnisse der FLORY-HUGGINSTheorie lassen sich wie folgt zusammenfassen: Die (erweiterte) FLORY-HUGGINS-Theorie dient dem Grundverständnis und als Grundlage zur Beschreibung von Polymerblends. Der darin auftretende FLORY-HUGGINS-Wechselwirkungsparameter ij wird als Maß für die thermodynamische Wechselwirkung zwischen den Polymeren verwendet. ij bestimmt den Grad der Mischbarkeit und die Gestalt von Phasendiagrammen. Im Gegensatz zu niedermolekularen Substanzen sind die meisten Polymere nicht oder nur partiell miteinander mischbar, weil der mit dem Mischungsvorgang einhergehende Entropiegewinn gering ist bzw. die wenigsten Systeme entsprechend niedrige Wechselwirkungsparameter ij aufweisen. Die Tendenz zur Mischbarkeit nimmt mit steigendem Polymerisationsgrad P ab. ij ist damit der entscheidende Parameter für die Beschreibung des Mischungsverhalten von Polymeren bzw. Polymer/Lösungsmittel-Systemen und dessen Kenntnis oder gegebenenfalls dessen Bestimmung von elementarer Wichtigkeit. ij ist jedoch nur in wenigen Fällen aufgrund des hohen experimentellen Aufwandes direkt bestimmt worden.[22] Es existieren verschiedene Möglichkeiten, ij aus experimentell besser zugänglichen Größen indirekt zu bestimmen oder abzuschätzen. Damit wird eine Voraussage bezüglich des Mischungsverhaltens möglich. Dies steht jedoch nicht mehr im Einklang mit dem zugrundeliegenden, ursprünglichen Gittermodell 7 Grundlagen 2.1.2 Löslichkeitsparameter Einen alternativen Ansatz zur Berechnung der enthalpischen Wechselwirkungen Hmix beschreibt HILDEBRAND[23]: 2 H mix i j V0ij (3) i und j sind eindimensionale Löslichkeitsparameter, V0 ein molares Referenzvolumen (Zellengröße des Gitters), welches häufig durch das geometrische Mittel der Molvolumina der einzelnen Komponenten definiert wird V0 V0,i V0, j , wobei V0,i M 0,i / i ist (M0,i = Molmasse des Lösungsmittelmoleküls bzw. der Grundeinheit der entsprechenden Polymerkette). Die Gleichung macht deutlich, daß die Löslichkeit (Mischbarkeit) mit kleiner werdender Differenz von i und j zunimmt. Es zeigt sich jedoch auch, daß nur Systeme mit positiver Mischungsenthalpie erfaßt werden. -Werte sind für eine Vielzahl von Verbindungen experimentell bestimmt und tabelliert worden. Darüber hinaus ist es möglich, -Werte aus Inkrementen der die Moleküle aufbauenden Gruppen zu berechnen. Der große Vorteil besteht darin, daß -Werte (nahezu) jeder Verbindung, insbesondere experimentell schwer zugänglicher, berechnet und vorausgesagt werden können. Diese eindimensionalen -Werte sind jedoch mit Fehlern behaftet, die bei unpolaren Verbindungen eher klein, bei polaren Verbindungen oder solchen, die Wasserstoffbrückenbindungen eingehen können, dagegen meistens groß sind. Weil das Modell der eindimensionalen HILDEBRANDschen Löslichkeitsparameter somit nur begrenzte Anwendung findet, wurde es durch HANSEN[24] weiterentwickelt: er berücksichtigte den Anteil von dispersiven, polaren und H-Brücken –Kräften, indem er den Löslichkeitsparameter aufteilte (dreidimensionale Löslichkeitsparameter): 2 d2 p2 H2 (4) E Koh , wobei EKoh = UVerd = HVerd – pV HVerd – RT . Die Kohäsionsenergiedichte EKoh kann aus V0 der Verdampfungswärme HVerd für Lösungsmittel direkt, für Polymere mit Hilfe von vergleichenden Quellungsoder Lösungsversuchen in Lösungsmitteln mit bekannter EKoh bestimmt werden. 8 Grundlagen Gleichung (3) geht dann über in H mix d ,i d , j 2 p ,i p , j 2 H ,i 2 H , j V0i j (5) d, p und H können experimentell nicht direkt bestimmt, wohl aber über Inkrementsysteme berechnet werden. Die vielversprechendsten[25] Ansätze stammen von HOY[26], und VAN KREVELEN/HOFTYZER[27]; ein alternativer, semiempirischer Ansatz stammt von KOENHEN/SMOLDERS[28], die - in Anlehnung an HANSEN - die Löslichkeitsparameter aus physikalischen Konstanten (nD und ) berechnet haben. Für die Temperaturabhängigkeit der Löslichkeitsparameter gilt nach UTRACKI[29]: 3 2 1 r T 293K exp S T T 293 3 2 3 2 13 6 (6) wobei Tr die reduzierte Temperatur und S1 eine universelle Konstante ist. Nach den verschiedenen Ansätzen wurden Löslichkeitsparameter von Polymeren und Lösungsmitteln, die im Rahmen dieser Arbeit verwendet wurden, bei zwei Temperaturen berechnet. Detaillierte Angaben befinden sich im Anhang (siehe Kapitel 7). Tab. 2-1: Löslichkeitsparameter, aus Gruppeninkrementen bzw. semiempirisch ermittelt Kompo- Methode nente PMMA PnBA PS p-Xylol v. Krevelen/Hoftyzer Hoy Koenhen/Smolders Mittelwert v. Krevelen/Hoftyzer Hoy Koenhen/Smolders Mittelwert v. Krevelen/Hoftyzer Hoy Koenhen/Smolders Mittelwert v. Krevelen/Hoftyzer Hoy Koenhen/Smolders Mittelwert d 20°C p 20°C H 20°C d 220°C p 220°C H 220°C [ MPa ] [ MPa ] [ MPa ] [ MPa ] [ MPa ] [ MPa ] 16,2 15,5 17,8 16,5 16,6 16,2 17,4 16,7 18,2 16,8 19,6 18,2 17,1 16,3 17,9 17,1 5,5 10,4 5,3 7,1 4,1 8,8 4,1 5,7 1,1 8,2 1,6 3,6 0,9 7,4 0,1 2,8 9,0 5,1 7,8 7,3 7,6 7,2 6,5 7,1 0,0 4,9 2,0 2,3 0,0 3,4 1,8 1,7 12,9 12,3 14,1 13,1 11,5 11,0 12,1 11,5 14,7 13,5 16,0 14,7 4,3 8,2 4,1 5,5 2,9 6,1 2,7 3,9 0,8 6,5 1,2 2,8 7,2 4,1 6,1 5,8 5,1 4,9 4,5 4,8 0,0 3,9 1,6 1,8 9 Grundlagen Es bleibt zu beachten, daß teilweise signifikante Diskrepanzen zwischen den verschiedenen Ansätzen herrschen und daß bei einigen anderen Systemen trotz großer Löslichkeitsparameter-differenzen Löslichkeit beobachtet wird und umgekehrt. Der Vergleich von Gleichung (2) mit Gleichung (5) liefert den gewünschten Zusammenhang zwischen ij und der experimentell zugänglichen Größe : ij d ,i d , j 2 p ,i p , j 2 H ,i 2 V0 H , j RT (7) Tab. 2-2a: ij-Werte für Polymer/Polymer-Systeme, aus Löslichkeitsparametern berechnet Polymer 1 Polymer 2 20°C 20°C 20°C vK/H Hoy K/S 20°C vK/H Hoy K/S 220°C PMMA PnBA PS 0,021 0,288 0,390 0,047 0,245 0,382 0,043 0,044 0,025 0,029 0,062 0,173 0,037 0,121 0,148 PnBA PS PMMA 0,039 0,674 1,007 0,071 0,057 0,065 0,073 0,422 0,505 220°C 220°C 220°C Bei HOY liegen die ij-Werte aller Systeme in der gleichen Größenordnung; ansonsten läßt sich folgender Trend erkennen: Aus Löslichkeitsparametern: PMMA / PnBA PnBA / PS PS/ PMMA Alle ij-Werte sind deutlich positiv; es ist zu erwarten, daß sich die jeweiligen Polymere nur zu einem extrem geringen Maße - PMMA/PnBA noch am besten, PS/PMMA am schlechtesten - miteinander mischen (ij >> 0,00277 , siehe Kapitel 2.1.1). Tab. 2-2b: ij-Werte für Polymer/Lösungsmittel-Systeme, aus Löslichkeitsparametern berechnet Polymer 1 Lösungsmittel 20°C 20°C 20°C vK/H Hoy K/S 20°C PMMA PnBA PS 0,127 0,186 0,031 1,022 0,811 0,012 2,598 2,148 2,771 0,498 0,444 0,025 p-Xylol p-Xylol p-Xylol Bei KOENHEN/SMOLDERS liegen die ij-Werte aller Systeme in der gleichen Größenordnung; 10 Grundlagen ansonsten läßt sich folgender Trend erkennen: Aus Löslichkeitsparametern: PS/ p Xylol PnBA / p Xylol PMMA / p Xylol p-Xylol ist für diese Polymere ein Lösungsmittel (ij << 2,77, siehe Kapitel 2.1.1), für PS das relativ beste, für PnBA und PMMA ein vergleichbar schlechteres. 2.1.3 Grenzflächenspannung Bringt man zwei (kondensierte) Phasen miteinander in Kontakt (Mischen), so wirkt an der Grenzfläche eine Kraft, die als Grenzflächenspannung bezeichnet wird. Wenn die Grenzflächenspannung ein negatives Vorzeichen hat, versucht das System die Grenzfläche zu vergrößern (Vermischung), wenn sie ein positives Vorzeichen hat, die Grenzfläche zu verkleinern (Entmischung). Die Grenzflächenspannung ist somit ebenfalls ein Maß für die thermodynamischen Wechselwirkungen zweier Phasen (vergl. FLORY-HUGGINS-Theorie). Werte für sind aufgrund des hohen experimentellen Aufwandes nur an wenigen Systemen bestimmt worden. Nach WU[30] kann aus den besser zugänglichen Oberflächenspannungen (unter Berücksichtigung disperser und polarer Anteile, wobei p ,i x p i und xp die Polarität ist) der einzelnen Komponenten - am besten aus dem harmonischen Mittel - berechnet werden: 1 2 4 d ,1 d ,2 d ,1 d ,2 4 p ,1 p ,2 p ,1 p ,2 (8) Tab. 2-3: Oberflächenspannungen Polymer xp PMMA PnBA PS 0,281 0,098 0,168 p-Xylol = 28,37.10-3 N/m 20°C d 20°C p 20°C - d/dT 220°C d 220°C p 220°C [10-3 N/m] [10-3 N/m] [10-3 N/m] [10-3 N/m K] [10-3 N/m] [10-3 N/m] [10-3 N/m] 41,1 33,7 40,7 29,6 30,4 33,9 11,5 3,3 6,8 0,076 0,070 0,072 25,9 19,7 26,3 18,6 17,8 21,9 7,3 1,9 4,4 11 Grundlagen Tab. 2-4: Grenzflächenspannungen Polymer 1 Polymer 2 PMMA PnBA PS PnBA PS PMMA 20°C [10-3 N/m] 220°C [10-3 N/m] exp,extrapol 220°C 4,59 1,42 1,50 3,13 1,40 0,96 n.b. 1,4 0,8 – 1,26 [10-3 N/m] Einen Zusammenhang zwischen und ij liefern die Ergebnisse von HELFAND und TAGAMI[31]: b2 ij 6 kT 2 (9) k ist die Boltzmann-Konstante und b die effektive Länge eines Grundbausteins[32] der Polymerkette. Durch Kombination der Gleichungen (8) und (9) können Werte für den FLORYHUGGINS-Wechselwirkungsparameter ij berechnet werden: Tab. 2-5: ij-Werte (20°C und 220°C), berechnet aus den Grenzflächenspannungen nach den Gleichungen (8) und (9) Polymer 1 Polymer 2 PMMA PnBA PS PnBA PS PMMA 20°C 220°C 1,700 0,162 0,182 0,278 0,056 0,026 Es läßt sich folgender Trend erkennen: Aus Grenzflächenspannungen: PS/ PnBA PS/ PMMA PMMA / PnBA Alle ij-Werte sind deutlich positiv; auch nach den auf diese Weise ermittelten ij-Werten ist es zu erwarten, daß sich die jeweiligen Polymere nur zu einem extrem geringen Maße miteinander mischen (ij >> 0,00277 , siehe Kapitel 2.1.1). Der hier zu beobachtende Trend (PS/PnBA noch am besten, PMMA/PnBA am schlechtesten mischbar) steht jedoch nicht im Einklang mit dem aus den Löslichkeitsparametern hergeleiteten Trend. 12 Grundlagen 2.2 Entmischung und Phasenbildung[33] Als Ausgangspunkt A eines Entmischungsprozesses wird zunächst ein Stadium der vollständigen Mischbarkeit gewählt. Dies kann zum einen eine verdünnte Lösung von Polymeren in einem gemeinsamen Lösungsmittel oder zum anderen ein bei erhöhter (für den Fall des UCST-Verhalten) Temperatur vollständig mischbares (lösungsmittelfreies) System sein. T Lösungsmittel A Einphasengebiet Einphasengebiet Entmischung Zweiphasengebiet Polymer 1 A Entmischung Zweiphasengebiet Polymer 2 Zusammensetzung Abb. 2-1: Darstellung des Entmischungsprozesses im Dreiecksdiagramm (links) bzw. Phasendiagramm (rechts) Wird nun Lösungsmittel entfernt bzw. die Temperatur erniedrigt (Bewegung vom Punkt A entlang des Pfeiles), so beginnt beim Überschreiten der Phasengrenzlinie(n), der Binodalbzw. der Spinodalkurve (siehe weiterführende Literatur[34]) der Entmischungsprozeß. Polymermoleküle diffundieren nun aus vermischten Regionen in entmischte, was zu einem entsprechenden Phasenwachstum führt. Dieser Prozeß verläuft mit abnehmender Lösungsmittelmenge bzw. Temperatur immer langsamer. Bei vollständiger Entfernung des Lösungsmittels bzw. nach Erreichen der Endtemperatur wird der Diffusionsprozeß durch die Diffusionskoeffizienten der einzelnen Makromoleküle kontrolliert. Da diese jedoch sehr klein (in der Größenordnung von 10-10cm2/s) bzw. die Viskositäten der Polymere sehr groß (103 1010Pa s) sind, ist ein weiteres Phasenwachstum erheblich erschwert. Die absolute Größe der Phasen wird durch die Zeit bestimmt, in der das System den Entmischungsprozeß durchläuft: bei langsamer Entfernung des Lösungsmittels bzw. bei moderater Temperaturerniedrigung "endet" das Phasenwachstum bei einer Phasengröße von ungefähr 100 - 101µm; bei einer schlagartigen Entfernung (z.B. flash-Verdampfung in 10-4s[35], 13 Grundlagen schneller Fällungsprozeß) oder durch Abschrecken des Systems kann dagegen die Phasengröße bis auf die molekulare Ebene hinab verringert werden. Das System ist nun jedoch sehr weit vom thermodynamischen Gleichgewicht entfernt und die Triebkraft für ein Phasenwachstum groß. 2.3 Rheologische Aspekte von Mischungsprozessen[36] Als Ausgangspunkt wird ein System mit makroskopischer Verteilung der Komponenten gewählt. Diese Situation findet man bei der Verarbeitung von Polymerblends in diskontinuierlichen oder kontinuierlichen (z.B. Extruder) Mischapparaten: nach dem Aufschmelzen der Komponenten entspricht die Phasengröße in etwa der eingesetzten Korngröße der Materialien (>> 101µm). Die durch Rühr-, Umwälz- und Mischwerkzeuge verursachten Scherungen und Dehnungen - in den aufgrund der hohen Viskositäten laminaren Strömungsfeldern - sorgen für eine Reduzierung der Phasengröße (dispersives Mischen) und eine gleichmäßige Verteilung der Komponenten (distributives Mischen). Gemäß TAYLOR[37] kann mit Hilfe der Weberzahl We für NEWTONsche Flüssigkeiten das Ausmaß von Deformation und Zerkleinerung kugelförmiger Tropfen (disperse Komponente) in einer Matrix abgeschätzt werden: D 16 M LB D We , D LB 16 16 M 19 wobei We M viskose Kräfte Grenzflächenkräfte (10) rD D ist die Deformation, L die Länge der großen Achse und B die Länge der kleinen Achse des deformierten Tropfens, D die Viskosität des dispergierten Tropfens und M die Viskosität der Matrix, die Schergeschwindigkeit und rD der Radius des kugelförmigen Tropfens. Die Grenzflächenkräfte stabilisieren den (kugelförmigen) Tropfen, die viskosen Kräfte sorgen dagegen für die Deformation bzw. Zerteilung des Tropfens. Wird ein Tropfen zerteilt, so vergrößert sich die Oberfläche der dispergierten Komponente und damit die Phasengrenzfläche zwischen den Komponenten. 14 Grundlagen Einen quantitativen Zusammenhang zwischen den entscheidenden Größen, der kritischen Weberzahl und dem Viskositätsverhältnis unter Berücksichtigung der Strömungsart liefert GRACE[38]: 10 4 We,krit. 10 3 10 2 10 Scherung 1 10 0 10 -1 Scherung und Dehnung 10 -2 10 -6 10 -4 10 -2 10 0 Viskositätsverhältnis Abb. 2-2: Abhängigkeit der kritischen Weber-Zahl vom Viskositätsverhältnis D/M Oberhalb der Grenzkurven kommt es zur Tropfenzerteilung ( We We ,krit ), unterhalb der Grenzkurven zur Deformation ( We We ,krit ). Die Zerteilung gelingt am leichtesten, wenn das Viskositätsverhältnis D/M 1 ist je kleiner die Grenzflächenspannung ist je größer der Tropfen, d.h. rD ist je größer die Schergeschwindigkeit ist wenn (neben Scherkräften) Dehnkräfte herrschen Es bleibt zu beachten, daß einige vereinfachende Annahmen gemacht wurden. So wurden die Wechselwirkungen verschiedener Tropfen nicht berücksichtigt. Eine Erhöhung der Schergeschwindigkeit führt zwar zu einer Erhöhung der Weber-Zahl, aber gleichzeitig zu einer größeren Wahrscheinlichkeit von Zusammenstößen und Vereinigungsprozessen der Tropfen. 15 Grundlagen Des weiteren handelt es sich in der Regel bei Polymerschmelzen nicht um Newtonsche Flüssigkeiten, sondern um viskoelastische Flüssigkeiten mit Strukturviskosität. Die Viskoelastizität führt zu einer Erhöhung der effektiven Grenzflächenspannung und stabilisiert damit den Tropfen. Das strukturviskose Verhalten erfordert eine Anpassung der Viskosität an die herrschende Schergeschwindigkeit. Die oben getroffenen Schlußfolgerungen bleiben jedoch qualitativ bestehen. Ebenso ist eine bestimmte Beanspruchungszeit notwendig, Tropfen zu deformieren oder zu zerteilen (Einstellung der Gleichgewichtslage); diese hängt wie auch die Weber-Zahl vom Viskositätsverhältnis ab. 2.4 Morphologie Die Eigenschaften heterogener Polymer/Polymer-Systeme sind eng an die Ausbildung bestimmter Strukturen während des Herstellungsprozesses der Polymermischung gebunden. Charakteristische Merkmale dieser Strukturen sind die Form, die Größe und die räumliche Verteilung der Komponenten (Morphologie des Systems). Die Morphologie ist zum einen von Stoffwerten der Komponenten (i, ij ,, i u.a.) und ihrer Zusammensetzung (i), zum anderen vom Herstellungsprozeß, d.h. von Betriebswerten (T, p, , u.a.) abhängig. Bezüglich der Form unterscheidet man bei binären Blends drei Typen: a) Polymer 1 bildet die Matrix und Polymer 2 die disperse Phase b) Polymer 1 und 2 bilden eine co-kontinuierliche Struktur c) Polymer 1 bildet die disperse Phase und Polymer 2 die Matrix a) 1 >> 2 b) 1 1 2 2 0,4 < c) 1 << 2 1 < 2,5 2 Abb. 2-3: Morphologien binärer Polymerblends in Abhängigkeit von der Zusammensetzung 16 Grundlagen Die Formen ternärer Blends werden durch eine weitaus größere Zahl an Typen beschrieben (siehe NAUMAN[39]). Grenzt man die Zahl in der Form ein, daß eine Komponente als Matrix definiert wird, während die beiden anderen die Unterschußkomponenten bilden, so kann die HARKINsche Gleichung[40] für das Spreitungsverhalten einer Flüssigkeit auf einer FestsubstratUnterlage auf ein polymeres Dreistoffgemisch übertragen werden.[41] Ausgehend von den Grenzflächenspannungen gilt für den jeweiligen Spreitungskoeffizienten der Unterschußkomponenten: 32 = 21 - 31 - 23 (11a) 23 = 31 - 21 - 32 (11b) 32 ist der Spreitungskoeffizient für die Komponente 3 auf der Komponente 2 (und entsprechend umgekehrt für 23), während Komponente 1 die Matrix bildet. Dann ergeben sich wiederum drei unterschiedliche Typen: a) Sind beide Koeffizienten 32 und 23 negativ, so bleiben die Phasen getrennt, d.h. Komponente 2 als auch Komponente 3 sind dispers und unabhängig voneinander verteilt b) Wenn 32 > 0 (und 23 < 0) ist, wird die Komponente 2 von 3 umhüllt. Sie bilden ein Kern-Schale-System mit Polymer 2 als Kern und Polymer 3 als Schale in der Matrix von Polymer 1 c) Wenn 23 > 0 (und 32 < 0) ist, wird die Komponente 3 von 2 umhüllt. Entsprechend bilden sie ein Kern-Schale-System mit Polymer 3 als Kern und Polymer 2 als Schale in der Matrix von Polymer 1 Matrix = Polymer 1 Polymer 2 Polymer 3 Matrix = Polymer 1 Matrix = Polymer 1 Polymer 2 Polymer 3 Polymer 3 Polymer 2 a) 32 < 0 b) 32 > 0 c) 23 > 0 23 < 0 23 < 0 32 < 0 Abb. 2-4: Morphologien ternärer Polymerblends in Abhängigkeit vom Spreitungskoeffizienten 17 Grundlagen Für das System PS/PMMA/PnBA können die Spreitungskoeffizienten mit Hilfe der Grenzflächenspannungen (siehe Tab. 2-4) ermittelt werden: Tab. 2-6a: Spreitungskoeffizienten (aus -Werten) für das System PS/PMMA/PnBA Matrix Polymer 2 Polymer 3 () Spreitungsverhalten PMMA PS PnBA PnBA PMMA PMMA PS - 3,57 + 0,77 - 2,69 - 3,57 + 0,77 - 2,69 PS und PnBA bilden ein Kern-Schale-System mit PnBA als Kern und PS als Schale PnBA und PMMA sind dispers und unab hängig voneinander verteilt PMMA und PS bilden ein Kern-Schale-System mit PMMA als Kern und PS als Schale PS PnBA PnBA PS PMMA PnBA PS PMMA Tab. 2-6b: Spreitungskoeffizienten (aus -Werten) für das System PS/PMMA/PnBA Matrix Polymer 2 Polymer 3 ( ) Spreitungsverhalten PMMA PS PnBA PnBA PMMA PMMA PS - 0,56 - 1,90 - 0,80 - 0,56 - 1,90 - 0,80 PS PnBA PnBA PS PMMA PnBA PS PMMA PS und PnBA sind dispers und unabhängig voneinander verteilt PnBA und PMMA sind dispers und unabhängig voneinander verteilt PMMA und PS sind dispers und unabhängig voneinander verteilt 2.5 Eigenschaften mehrphasiger Polymerblends: Zusatz und Wirkungsweise von Haftvermittlern[42] Nicht miteinander mischbare Polymerblends bilden separierte Phasen von makroskopischer Größenordnung. An den Phasengrenzen herrschen hohe Grenzflächenspannungen, und die Adhäsion ist im Vergleich zu den Hauptphasen stark vermindert. Bei Beanspruchung des Materials werden die Phasengrenzen zu bevorzugten Riß- oder Bruchstellen. Große Domänen (Teilchengrößen) wirken sich dabei besonders negativ aus. Das Eigenschaftsprofil solcher Blends ist eher mäßig. Zur Verbesserung der strukturellen Integrität und damit der Produkteigenschaften dienen sogenannte Haftvermittler. Als Haftvermittler eignen sich - in Analogie zur verbesserten Dispersion von Öl in Wasser durch den Zusatz von Tensiden - grenzflächenaktive Substanzen auf makromolekularer Basis, d.h. Copolymere mit amphiphilem Charakter. -Werte können mit Hilfe von Gleichung (9) und Tab. 2-2a berechnet werden 18 Grundlagen Diese Haftvermittler wirken auf verschiedene Weise: Sie verlangsamen die Entmischung und das Phasenwachstum (kinetische Stabilisierung). Sie bilden eine schützende Hülle und verhindern die Vereinigung von Tropfen (siehe Kapitel 2.2). Sie setzen die Grenzflächenspannung herab. Haftvermittler nehmen dadurch direkten Einfluß auf die thermodynamischen Wechselwirkungen. Die Triebkräfte für eine Phasenentmischung sind geringer (siehe Gleichungen (2), (9) und Kapitel 2.1). Sie erhöhen die Adhäsion zwischen den Phasen. Oberhalb der Verschlaufungsmolmasse können sich die Haftvermittlermoleküle mit den Polymermolekülen der Hauptpolymerphase durchdringen und verhaken. Der Zusammenhalt zwischen den Phasen wird dadurch größer ("Schnürsenkelprinzip"). Sie ermöglichen, daß die Basispolymere in kleinere Domänen zerteilt werden. Nach Gleichung (10) ist es - unter ansonsten gleichen Bedingungen - aufgrund der geringeren Grenzflächenspannnung einfacher, Tropfen zu zerteilen (siehe Kapitel 2.3). Morphologieentwicklung ohne Zusatz von Haftvermittler Morphologieentwicklung mit Zusatz von Haftvermittler Abb. 2-5: Schematische Darstellung zur Wirkungsweise von Haftvermittlern Die größte Effizienz zeigen Diblockcopolymere, mit denen insbesondere binäre Blends direkt haftvermittelt werden können (PA/PA-b-PB/PB). Eine Erweiterung stellt die Verwendung zweier Diblockcopolymere dar, die jeweils aus einem Block der Hauptpolymerphase und 19 Grundlagen einer weiteren Komponente C bestehen (PA/PA-b-PC/PC-b-PB/PB). Wenn sich diese beiden Diblockcopolymere über die Blockkomponente C zusammen anordnen, sollten sie sich wie ein einzelnes Diblockcopolymer PA-b-PB verhalten; sie enthalten eine Pufferschicht C und wirken indirekt haftvermittelnd. Der schematische Ausschnitt aus der näheren Umgebung der Phasengrenzfläche verdeutlicht dieses System, angewendet auf die Polymere PMMA, PnBA und PS und die entsprechenden Haftvermittler PMMA-b-PS und PnBA-b-PS: PMMA PMMA-b-PS PS-b-PnBA PnBA PS Abb. 2-6: Schematische Anordnung von PMMA, PnBA (und PS) bei Zusatz von Haftvermittlern 20 Grundlagen 2.6 Herstellung von Polymerblends[43] Polymerblends können durch mechanisches Mischen von Schmelzen, Latices oder Lösungen zweier separat hergestellter Polymerer oder durch in-situ Polymerisation hergestellt werden. Alle vier Verfahren haben bestimmte Vor- und Nachteile in Bezug auf die Verfahrensführung, die Wirtschaftlichkeit und die Endeigenschaften der Produkte. Beim Lösungsmischen werden die Polymere in einem gemeinsamen Lösungsmittel gelöst und liegen auf molekularer Ebene verteilt vor. Die anschließende Entfernung des Lösungsmittels (Verdampfen, Fällen) liefert die Polymermischung. Besondere Bedeutung kommt den Wechselwirkungen zwischen Lösungsmittel und den einzelnen Polymeren zu. Beim Schmelzmischen werden die Polymere über ihre Glas- bzw. Schmelztemperatur erwärmt und durch Walzen, Kneten oder Extrudieren, d.h. unter dem Einfluß von Scher- und Dehnkräften, vermischt. Rheologische Aspekte der Blendaufbereitung und thermodynamische Wechselwirkungen zwischen den Polymeren stehen im Vordergrund. Beim Latexmischen werden wässrige Dispersionen der beiden Polymeren miteinander gemischt. Die Polymermischung erhält man durch Koagulation des Latex oder durch Abtrennung des Wassers. Bei der in-situ Polymerisation wird ein Monomer, in dem schon vorgebildetes Polymer gelöst ist, polymerisiert. Diese Mischverfahren haben je nach Wahl der Mischungsbedingungen einen großen Einfluß auf die Morphologie und damit auf die Eigenschaften der entstehenden Blends. Dies gilt besonders für solche Polymerblends, bei denen die Einzelkomponenten nur eine minimale Mischbarkeit aufweisen (heterogene Polymer/Polymer-Systeme). 21