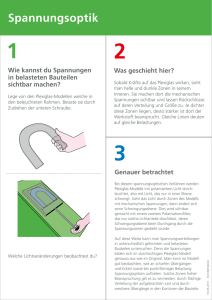
Vorlesung Teil Hydrostatik/Hydrodynamik (MS
Werbung

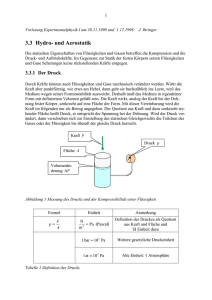
Hydrostatik, -dynamik Bisher waren die untersuchten Körper fest und unverformbar. Das muss natürlich nicht so sein (Z.B. Wasser) Da die Materie ihre Form beliebig ändern kann und sich die Eigenschaften einer Flüssigkeit nicht ändern, ob man nun viel oder wenig nimmt (Masse egal) führt man die Dichte ein Dichte = m/V [kg/m3] Weiterhin: Eine punktförmig angreifende Kraft macht keinen Sinn (Flüssigkeit weicht aus). Kraft pro Fläche sinnvoller Druck p = F/A [Pa] = [N/m2] A : Fläche 1 Andere Druckeinheiten: 1bar = 105 Pa 1atü = 9.806104 Pa 1 torr = 1mmHgSäule = 133.32 Pa (wird z.B. noch bei Blutdruckmessungen angegeben) gemessen wird mit Manometern (Flüssigkeitsdruck) oder Barometern (Luftdruck) Annahme: Flüssigkeitsbox in der Schwerelosigkeit, ein Kolben kann von einer Seite drücken. F 2 Da sich die Flüssigkeit im Gleichgewicht befindet, müssen von überall die gleichen Kräfte wirken (alle Kräfte kompensieren sich zu 0). d.h. die „Kraftdichte“ (also der Druck) ist in allen Richtungen gleich und konstant. Der hydrostatische Druck (in Schwerelosigkeit) ist in allen Richtungen gleich und konstant Kommunizierende Röhren: Obwohl die Masse der Flüssigkeiten in den verschiedenen Röhren verschieden ist, ist der Flüssigkeitsstand über gleich. Grund: Druck ist gleich (F/A) 3 Versuch: Hydraulische Presse hydrostatischer Druck ist im Gleichgewicht überall gleich: Fg1 A1 A2 Fg2 p = Fg1/A1 und p = Fg2/A2 Also : Fg1 A1 Fg 2 A2 Aber auch hier kann man nicht Arbeit gewinnen oder sparen (vergleiche Hebel): Wenn an (1) die Höhe h1 heruntergepresst wird, dann wurde das Volumen V=A1h1 verdrängt. Das selbe Volumen presst (2) hoch, also V=A2h2 = A1h1 also: 4 A1 Fg 2 A1h1 A2 h2 W1 m1 gh1 Fg1h1 h1 Fg 2 Fg 2 h2 Fg 2 W2 A2 A2 A2 Druckarbeit: W=mgh = Vgh = pV (bei konstantem Druck) Arbeiten sind gleich. Wichtig: Flüssigkeiten sind (so gut wie) inkompressibel. (Druck ändert das Volumen kaum) Anwendung ist Hydraulische Hebebühne, man kann im Gegensatz zum Hebel beliebige Distanzen überbrücken, indem man beliebig viel Hydrauliköl ins System pumpt. Versuch höhenabhängiger Wasserdruck (Schweredruck) Wasserdruck ist höhenabhängig 5 Eine Wassersäule mit der Dichte der Höhe h und dem Querschnitt A hat die Gewichtskraft F = mg = Vg und das Volumen V=Ah also gilt für den Druck: p = F/A = Vg/A = gh p(h)=gh Versuch Tiefendruck Druck ändert sich mit der Höhe. Zeigt aber auch, dass abgesehen von der Höhe der Druck konstant ist: Drehen des Druckmessers (Manometer) : gleicher Druck. 6 Konkret: Z.B. Wasser (Dichte H2O=1g/cm3 = 1000kg/m3) p = H2Ogh mit h=10.3m : p = 1013hPa = 1013mbar 1bar Luftdruck. D.h. je 10m Wassertiefe steigt der Druck um 1bar (eine Luftdruckeinheit) da Druck (auch Luftdruck) aber allseitig wirkt, heißt das aber auch: 1) auf der Erde ist der tiefenabhängige Wasserdruck (Wassertiefe h) p(h) = p0 +H2Ogh p0 : Luftdruck Wasser 2) Der Luftdruck kann eine 10 hohe Wassersäule tragen. Vesuch Becher randvoll mit Wasser. Abdecken mit Mauspad und umdrehen. Wasser läuft nicht aus. 7 3) Mit einer Saugpumpe (Z.B. Handschwengelpumpe) können maximal 10m hoch gepumpt werden. Grund: eigentlich wird über dem Wasser evakuiert, sodass von oben kein Luftdruck mehr wirkt [p(h)=0], von unten [p(0)=1013hPa] wird das Wasser max 10m hochgedrückt. 4) nimmt man statt Wasser Quecksilber (Hg=13587kg/m3), so kann eine 760mm Säule vom Luftdruck getragen werden h Vakuum, wenn h die entsprechende Höhe einstellen kann Die tatsächliche Höhe h ergibt sich aus dem Luftdruck. Quecksilberbarometer 8 Eine Änderung des Luftdrucks von p1=1013hPa auf p2= 1000hPa hätte eine Höhenänderung von: p1-p2=p0+Hggh1-(p0+Hggh2) = Hggh h=(p1-p2)/Hgg=9.7mm zur Folge. Auftrieb (Archimedisches Prinzip) Eintauchen des Vollzylinders: Waage hebt sich, Füllen des Hohlzylinders: Waage wieder im Geichgewicht Vollzlinder verdrängt diese Menge Wasser 9 H fl k A p1 p2 Auf den Körper mit der zylindrischen Grundfläche A wirkt die Gewichtskraft Fg=-mkg =-kVg = -gkAH Druckdifferenz in Flüssigkeit: p=p2-p1=gfl(H2-H1)=gflH Also wirkt auf den Körper die Druckkraft: Fp= pA = gflAH a) Dichte des Körpers ist größer als Dichte der Flüssigkeit also: |Fg| > |Fp| Körper geht unter b) Dichte des Körpers gleicht der Dichte der Flüssigkeit also: |Fg| = |Fp| Körper schwebt in Flüssigkeit c) Dichte des Körpers ist kleiner als Dichte der Flüssigkeit also: |Fg| < |Fp| Körper steigt auf 10 Fall c) Schwimmen. Wenn der Körper auftaucht und aus der Flüssigkeit schaut, dann muss die Druckdifferenz von der Flüssigkeitsoberfläche aus genommen werden: Bei Eintauchtiefe h Gleichgewicht zwischen Fg und Fp möglich : Fg+Fp=0 : gkAH = gflAh also kVk = flVverdr. Flüss. mk = mverdrFl Ein Körper schwimmt, wenn er seine eigene Masse Flüssigkeit verdrängt hat. Druck in Gasen wichtigster Unterschied zu Flüssigkeiten: Gase sind stark kompressibel. D.h. Druckänderung hat Volumenänderung zur Folge. 11 Kompressibiltät : = -(1/V)V/p = -(1/V)dV/dp a) Drücke 1Liter Wasser ( h2o=510-10m2/N ) mit 1bar zusammen. also p = 1bar = 105Pa V = 1l = 10-3m3 V = -Vp = 510-8m3 = 5010-9m3 = 50(mm)3=50l (Würfel von 3.7mm Kantenlänge). Wasser ist so gut wie inkompressibel. b) für Gase gilt das Gesetz von Boyle-Mariotte Vp = const (das Produkt aus Volumen und Druck ist konstant) also: V = const/p dV/dp = -const/p2 und somit die Kompressibilität : = -(1/V)dV/dp = 1/(Vp)const/p = 1/p 12 D.h. die Kompressibiltät ist umgekehrt proportional zum Druck (je stärker ich drücke, desto weniger presse ich das Volumen zusammen). presse 1l Luft von 1bar auf 2bar zusammen: V1p1=V2p2 also V2=V1p1/p2 = 0.5l Beim Komprimieren ändert sich die Dichte. ALSO p(h) = gh gilt nur für Flüssigkeiten, (bei denen die Dichte trotz Druckerhöhung [fast] konstant bleibt). Annahme: Würde das Gesetz gelten (Luft, Luftdruck = 1.29kg/m3) dann wäre bei h = p/(gLuft, Luftdruck) = 8000m die Athmosphere zuende!! (Mount Everest ca 8800m hat noch 1/3 Normaldruck). 13 Wie sieht der höhenabhängige Atmosphärendruck tatsächlich aus? Annahme: für winzige Druckänderungen / Höhenänderung gilt p(h) = gh noch in der Form p = -(h)gh (1) (Minuszeichen bei Athmosphere, da die Höhe andersrum [nach oben] zählt, als bei Wasser [nach unten]) weiter gilt : (h) = m(h)/V(h) Man kann jetzt natürlich die Massenänderung in die Volumenänderung stecken. d.h. es werden immer die selben Massen m0 betrachtet. Also (h) = m0/V(h) (2) ist möglich. 14 nach Boyle-Mariotte gilt pV = const = p0V0 sei z.B. p0 der Luftdruck auf der Erdoberfläche und V0 =V(0) das entsprechende Volumen, dass die Referenzmasse m0 einnehmen würde. Also V = p0V0/p (3) (3) in (2) : (4) in (1) : (h) = m0/V = pm0/(p0V0) = p0/p0 p = - pg(0/p0)h (4) dp/p = - g(0/p0)dh Einmal durchintegrieren: dp/p = -g(0/p0)dh lnp(h) = -g(0/p0)h also : p(h) = p0exp[-g(0/p0)h] 15 Exponentieller Abfall des Athmosphärendrucks: p p0 Druck nimmt alle 9000m um ca 1/3 ab: In 90km Höhe 1/310p0 also etwa 1mbar h Beispiel Kartesisches Teufelchen Druck auf die Flüssigkeit verändert Schwebehöhe des Teufelchens. Grund: Druck führt zur Volumenänderung des Tauchers. Auftrieb ändert sich. 16 Beispiel: Helium gefüllter Ballon Unter Wasser würde ein z.B. mit Öl gefüllter Ballon nicht funktionieren, er würde einfach bis zur Oberfläche aufsteigen. (Verdrängte Masse wäre immer gleich, Auftrieb immer gleich) In der Athmosphere steigt ein Helium gefüllter Ballon bis zu einer bestimmten Höhe Annahme: Gesamtmasse Ballon mB=300kg. Luft,p0 = 1.29 kg/m3 He,p0 = 0.178 kg/m3 Damit auf der Erdoberfläche der Ballon gerade schwebt, muss der Auftrieb (Masse der verdrängten Luft) gerade die Gesamtmasse des Ballons [300kg+Masse des Heliums] betragen: 17 mLuft,p0 = mB+mHe,p0 Luft,p0V = mB+He,p0V also Vp0 = mB/(Luft,p0-He,p0)=270m3 Kugel mit D=8m Annahme: Man möchte 1000m hoch fliegen. Wie groß muss die Kugel sein? Der Luftdruck in 1000m Höhe ist p(h) = p0exp[-g(0/p0)h] = 894mbar = 89.4kPa Der selbe Druck herrscht im Ballon Boyle-Mariotte : pV = p0V0 also : = (0/p0)p pm0/ = p0m0/0 Für Luft Luft,1km = 1.14kg/m3 , für He : He,1km = 0.157kg/m3 also V1km = mB/(Luft,1km-He,1km)=305m3 Kugel mit D=8.35m 18 Oberflächenspannung, Kapillarität Dazu wichtiger Satz vorweg: Ein System versucht im Gleichgewicht immer den Zustand geringster Energie anzunehmen. Bei einem System mit Reibungskräften wird dieser Gleichgewichtszustand geringster Energie auch tatsächlich angenommen. Beispiel: Hüpfender Ball in geschlossener Box. Ball versucht immer in Richtung Erdoberfläche zu fallen. Im vollständig elastischen Fall springt er allerdings immer wieder hoch. Im inelastischen Fall kommt er dagegen irgendwann am Boden zur Ruhe (Gleichgeichtszustand minimaler Energie) 19 Konzept der Oberflächenspannung: Flüssigkeit besteht aus Teilchen (Molekülen), die sich gegenseitig anziehen. Im Volumen ist jedes Molekül symmetrisch von anderen Molekülen umgeben: Kräfte addieren sich zu NULL An der Oberfläche fehlen Moleküle: Resultierende Kraft nach innen. Fres=0 Fres0 d.h.: Moleküle an der Oberfläche werden in das Volumen hineingezogen. 20 Oberflächenenergie ist Esurf = A mit : Oberflächenspannung, A Fläche. Konvention: Die Oberflächenspannung wirkt ENTLANG der Oberfläche z.B. Wasser h2o = 0.073 N/m Versuch: Eingeölte Büroklammer schwimmt auf Wasseroberfläche grob vereinfachte Skizze D Esurf Epot L Esurf klein, Epot groß D Esurf Epot L Esurf groß, Epot klein 21 Zylinder, D=0.5mm Durchmesser, L=10cm Länge V=(D/2)2L = 210-8m3 A = dL = 1.5710-4m2 Dichte von Eisen: Fe=7700 kg/m3 also mBk=FeV = 0.154g Wenn Büroklammer komplett eingetaucht ist: zusätzlich Esurf = h2oA 10-5 J Dafür potentielle Energie kleiner EpotmBkgD10-6 J Der Verkleinerung der Potentiellen Energie macht die Vergrößerung der Oberflächenenergie nicht wett: Büroklammer geht nicht unter!! Wenn man sie allerdings einmal untergetaucht hat, sinkt sie zu Boden, weil keine Kraft in Richtung Oberfläche wirkt. 22 Versuch : Druck in Seifenblase Kleine Seifenblase bläst große auf, da Überdruck in Blase proportional zu 1/r ist !! R Volumen: V=4/3R3 Oberfläche : A = 4R2 aus Volumen: R V 1/ 3 R 4 3 p also : A = 4 R 4V 2/3 1 3 4 3 2 3 23 Gesamtenergie der Seifenblase mit Außenradius R (wenn R << R, 2 Oberflächen!!!) W = E = 2(4R ) = 2A = 2 4V 2 4 4 4 p R 3 3 3 3 4 3 W = -pV Druckarbeit war definiert als 2 1/ 3 4 p= -dW/dV=2 4 V 3 3 2/3 2 3 2 3 W/V = -p 1 3 24 1 4 2 4 R 33 3 4 R In kleinerer Seifenblase herrscht größerer Überdruck!! 24 2 3 Kapillarität (Kapillarkräfte) Versuch Kapillarkräfte: Werden Glasröhren in Wasser gehalten, so steigt das Wasser hoch, je dünner die Röhre, desto höher. Grund auch hier ein minimales Gleichgewicht zwischen Oberflächenenergie und potentieller Energie. Annahme: Auf der Innenwand der Röhre bildet sich ein ganz dünner Benetzungsfilm. mfl Vfl d h 25 Durch Aufsteigen der Flüssigkeit verringert sich die Oberfläche um A=dh (Zylinderabschnitt, schwarze Linien). D.h. die Oberflächenenergie verringert sich um Esurf = A = dh Allerdings erhöht sich die potentielle Energie um Epot=mflgh = Vflflgh= (hd2/4) flgh Gleichgewicht hat man, wenn beide Energien gleich sind: dh = gh2fld2/4 4=ghfld h=4/(gdfl) z.B. Kapillare mit 1mm Durchmesser, Wasser: h=3cm 26 Beispiel: Form der Flüssigkeitsoberfläche an Gefäßwand Vereinfachung: schräger Abschnitt, keine Idealkurve Epot H h H h L : Länge der Wand Gesamtenergie links: E = HL+HL = 2HL 1 Gesamtenergie rechts: E 2 L( H h) 2Lh gLh3 6 2 2 Energie wird minimal bei h = 4.5mm für Wasser g 27 Grenzflächenspannung Eigentlich ist das Konzept der Oberflächenspannung ungenau: Es liegt zumeist auch Materie auf der Oberfläche (Luft, Gas, Festkörper) aber mit anderen Wechselwirkungen als in der Flüssigkeit. Fres0 Materie 1 Fres=0 Materie 2 Einführung der Grenzflächenspannung 12 28 Beispiel: Bei einem Flüssigkeitstropfen auf einer festen Platte gibt es DREI Grenzflächenspannungen: (1) Platte – Flüssigeit (2) Platte – Dampf (bzw Luft) und (3) Flüssigkeit – Dampf (bzw Luft). Das Verhältnis dieser drei Spannungen (pf , pd , fd) bestimmt, ob und wie eine Substanz benetzt wird: pd pf = fdcos() : Benetzungswinkel 1) Vollständige Benetzung (Tropfen zerläuft) wenn pd pf > fd (kein möglich) 2) Teilweise Benetzung (Tropfen kontaktiert Platte) fd > pd pf > fd 3) Keine Benetzung: fd > pd pf 29 Hydrodynamik Fließende Flüssigkeit ist äußerst kompliziert: a) Man kann keine „einfache“ Geschwindigkeit definieren. Statt dessen ist die Geschwindigkeit i.a. vom Ort und von der Zeit abhängig (Stromlinien und Bahnlinien) Bahnlinien: wo befindet sich ein Teilchen zu welchem Zeitpunkt Stromlinien: mit welcher Geschwindigkeit bewegt sich ein Teilchen am Ort (x,y,z) Bei stationären Flüssigkeiten (Geschwindigkeiten sind zwar orts- aber nicht zeitabhängig) sind Bahn und Flusslinien identisch. 30 Bahnkurven schwarz, Flusslinien die verbundenen Tangenten der magenta Linien 31 b) Teile der Flüssigkeit können von a nach b fließen oder auch immer nur im Kreis (Rotation) c) Die Flüssigkeit kann kompressibel sein d) Es kann innere Reibung geben (Viskosität ) Es sollen jetzt nur ideale Flüssigkeiten untersucht werden: keine Kompressibilität, keine Viskosität Dicke x1 Dicke x2 p1, u1 p2 , u2 Fläche A1 Fläche A2 Volumen muss beim Durchströmen erhalten bleiben (inkompressibel), also: V1/t = V2/t A1x1/t = A2x2/t A1u1 = A2u2 ui : Geschwindigkeiten 32 D.h.: wenn sich ein Rohr verjüngt, erhöht sich die Durchflussgeschwindigkeit. D.h. aber für die kinetische Energie der bewegten Massen: Ekin,1 = ½ m1u12 = ½ Vu12 Also für A 2 < A1 : und Ekin,2 = ½ m1u22 = ½ Vu22 u2 > u1 : Ekin,2 > Ekin,1 Natürlich gilt auch hier Energieerhaltung. D.h. die zusätzliche Kinetische Energie Ekin=Ekin,2-Ekin,1 muss von irgendwo herkommen, nämlich aus der Druckarbeit W = -pV W=W2 -W1 = (p1-p2)V = Ekin = Ekin,2 - Ekin,1 = ½ V(u22 –u12) 33 Also gilt: p1V + ½Vu12 = p2V + ½Vu22 p1 + ½u12 = p2 + ½u22 dieses ist nun für alle möglichen Kombinationen p1, p2 richtig also gilt allgemein: p + ½u2 = p0 = const im Gravitationsfeld kann man den ersten Term noch auftrennen in „künstlich angelegten Druck“ und „Schweredruck“: p + gh + ½u2 = const sog Bernoulli-Gleichung (Energiesatz für Flüssigkeiten) 34 Anwendung: Wie schnell strömt Flüssigkeit aus einem kleinen Loch. Versuch höhenabhängiger Wasserdruck (Schweredruck) Wasserdruck hat verschiedene Ausströmgeschwingkeiten zur Folge p0 x h Wenn Loch klein ist: x sehr klein, d.h. u10 und hinter Loch ist p2 0 (p0 : Luftdruck) p0 + gh + 0 = p0 + 0 + ½u2 also: u = (2gh)½ 35 Ausströmgeschwindigkeit bei Druck mit Kolben: p x Wenn Loch klein ist: x sehr klein, d.h. u10 und hinter Loch ist p2 0. p + 0 = 0 + ½u2 also: u = (2p/)½ Weitere Bernoulli- Experimente (bei Verengung sinkt der Druck, bei Erweiterung steigt er) Untere Platte wird angezogen (Querschnitt steigt, Druck steigt Druck an der Verengung ist kleiner 36 Auftrieb bei Flugzeugflügel: a) symmetrischer Flügel v1, p1 v,p v1, p1 Luft strömt mit Geschwindigkeit v auf Flügel, Verengung der Flusslinien nahe der Flügeloberfläche höhere Geschwindigkeit v1 an den Flügeloberflächen Druckerniedrigung am Flügel, aber symmetrisch (oben und unten) kein Auftrieb 37 b) asymmetrischer Flügel v1 , p1 v,p v2 < v1 also p2 > p1 Luft strömt mit Geschwindigkeit v auf Flügel, Verengung der Flusslinien nahe der Flügeloberfläche höhere Geschwindigkeit v1,v2 an den Flügeloberflächen aber unten weniger verengt, d.h. v1 > v2 oben niedrigerer Druck als unten Sog nach oben. 38 Versuch: Auftrieb mit rotierendem Ball Ball kann mit Pressluft schräg angeblasen werden und bleibt in der Luft „hängen“ wenn er dabei rotiert. Grund: Der Ball reißt Luft mit, oben wird die Geschwindigkeit schneller,unten langsamer (Magnus Effekt) Auftrieb nicht rotierend kein Auftrieb rotierend Auftrieb 39 Nichtideale Flüssigkeit (innere Reibung, Viskosität) Bei einer idealen Flüssigkeit (Viskosität =0) können sich die Flüssigkeitsvolumina unabhängig voneinander bewegen. An der „Grenzfläche“ zwischen beiden gibt es kein Beeinflussung beider Teile. Sie gleiten aneinander vorbei. Reale Flüssigkeit: Moleküle beeinflussen sich untereinander: unmöglich real 40 Flüssigkeitsmoleküle „reiben“ aneinander oder an Wänden Anderes Beispiel: Feste Wand mit Flüssigkeitsfilm der Dicke z. Darauf gleitet eine Platte der Fläche A mit der Geschwindigkeit u. Um die Geschwindigkeit aufrecht zu erhalten benötigt man eine ständig wirkende Kraft F F A u z Wand ruht An der Wand haben die Flüssigkeitsmoleküle die Geschwindigkeit 0 an der bewegten Platte u. Dazwischen ein lineares Geschwindigkeitsprofil und es gilt: u du mit : Viskosität ( allgemeiner F A ) F A z dz 41 Viskosität ist für Flüssigkeiten relativ stark temperaturabhängig, da „heisse“ Moleküle weniger miteinander wechselwirken (und besser aneinander vorbei gleiten) z.B. Wasser 0°C = 1.82 (mN)s/m2 = 0.0182 Poise = 18.2mP 20°C = 1.03 (mN)s/m2 = 10.3 mP 100°C = 0.29 (mN)s/m2 = 2.9 mP (T) exp(b/T) oder Glyzerin : oder Luft: glyc = 1.53 Ns/m2 Luft = 17(N)s/m2 Beispiel:Flüssigkeit strömt durch Rohr (Länge L, Radius R) p1 R L p2 r 42 Für die Reibungskraft an einem Sub-Zylinder mit Radius r muss gelten: Fr = AM(du/dr) : AM Mantelfläche = 2rL ist im Gleichgewicht identisch zu der Druckkraft auf den SubZylinder: Fp = (p1-p2)AK : AK Kopffläche = r2 also : 2rLdu/dr = (p1-p2)r2 du/dr = r(p1-p2)/(2L) integrieren: u(r)=(r2/2)(p1-p2)/(2L)+u0 Bedingung u(R)=0 also u(r)=(r2-R2)(p1-p2)/(4L) 43 D.h. Parabolisches Geschwindigkeitsprofil, das Rohr wird nicht vollständig für den Materietransport ausgenutzt. Aussen wird weniger Materie transportiert als innen. Der Materialtransport dV/dt (Volumen pro Zeit) ergibt sich zu: R ( p1 p2 ) R 4 dV u (r ) 2rdr Hagen-Poiseuille dt 0 8L Verdoppelt man also den Rohrdurchmesser, dann kann man bei gleicher Druckdifferenz die 16fache Menge Flüssigkeit hindurchpumpen. Versuch Stokes’sche Reibung: Kugeln mit Radius r sinken in zähflüssigem Öl mit konstanter Geschwindigkeit. Die Kugel reisst Flüssigkeit etwa im Abstand r von der Oberfläche Flüssigkeit mit (also z von oben etwa r ) 44 fallende Kugel r ruhende Flüssigkeit ruhende Flüssigkeit also F 4r2u/r = 4ur genaue Rechnung (Gesetz von Stokes) ergibt: F=6ur Also gilt für konstant sinkende Kugel der Masse m (Dichte k) in der Flüssigkeit mit der Dichte fl : Gewichtskraft-Auftrieb = Stokes : 4/3r3(k-fl)g=6ur also u 2 g ( k fl )r 2 9 45 also : je größer Kugel, je schwerer sie ist und je weniger viskos und je leichter die Flüssigkeit, desto schneller sinkt die Kugel. z.B. Luft, r = 20cm Mensch = 1000kg/m3 also u 20*1000*0.04/10/ 20e-6 4e6 m/s völliger Quatsch, da Gesetz nur für langsame Strömungen gilt!! (laminar) Für schnellere Strömungen (Schiff, Turbolenzen erlaubt): u 3 fl Prandtl-Reibung: F A r 1 oder extrem turbolent Newton-Reibung : F cw fl Au 2 2 (cw,Kugel 1 , keine Abhängigkeit von , umensch,luft100m/s) 46 d.h.: Der Strömungswiderstand ist bei laminarer Strömung wesentlich kleiner (Kraft = constu) als bei turbolenter Strömung (Kraft = konstu2). Blutadern sind z.B. so dimensioniert, dass Strömung laminar ist. Versuch turbolente + laminare Strömung (mit Zigarettenrauch) Bei kleiner Gasgeschwindigkeit: Stromlinien wohldefiniert und statisch: Laminar Bei großer Gasgeschwindigkeit: Stromlinien nicht wohldefiniert und zeitlich veränderlich: Turbolent 47 Abschätzung wann laminar und wann turbolent durch sog. Reynolds-Zahl Re = fluX/ X : typische Systemlängenskala (z.B. Rohrdurchmesser, Kugeldurchmesser) Ist Re größer als ein (systemabhängigiges) Rekrit , dann hat man turbolente Strömung, sonst laminare. z.B. für Rohre gilt allgemein: Rekrit 1000 für Rohre ist X = Durchmesser des Rohrs d.h. für Wasser in einem 1cm starken Rohr gilt: ukrit = Rekrit/(fld) (1e-31000/(10000.01))m/s = 0.1m/s 48 Für alle Geschwindigkeiten oberhalb ukrit bilden sich Turbolenzen. Also folgende Bedingungen für laminare Strömung: a) kleine Systemsabmessungen (Wirbel passen nicht ins System) b) grosse Viskositäten (Wirbel werden durch innere Reibung stark gedämpft) c) kleine Durchflussgeschwindigkeiten (Wirbel können sich gar nicht erst ausbilden) d) kleine Dichten der Flüssigkeit 49 Kurzer Abriss: Deformierbarer Körper Wird an einem Faden (Länge L, Querschnitt A, Durchmesser D) mit der (nicht zu großen) Kraft F gezogen, so dehnt er sich elastisch um L: L = (1/EM)L(F/A) oder L/L = (1/EM)(F/A) EM ist der sog. Elastizitätsmodul (für Metalle typischerweise EM 100109N/m2 ) z.B. 1m langer Cu-Draht mit 1mm2 Querschnitt dehnt sich bei Belastung mit 1kg um (1/(100109))19.81/10-6 m 0.1 mm Auch das Volumen kann sich leicht änderen: V/V = [(1-2)/EM](F/A) : Poisson Zahl [0.15...0.5] 50 = 0.5 : Volumen ändert sich nicht. Zusammenhang mit der Kompressibilität: = 3(1-2)/EM Man kann einen Körper auch scheren. Der Körper verbiegt sich um einen Winkel mit F = (1/GM)(F/A) A GM : Torsionsmodul (Schubmodul) Zusammenhang mit EM und : EM = 2G(1+) 51