Document

Die mechanischen Eigenschaften der Flüssigkeiten
• Flüssigkeiten besitzen keine bestimmte Gestalt und können sich jeder
beliebigen Gefäßform anpassen.
• Es treten keine gestaltselastischen Verformungen wie Scherungen,
Torsionen oder Biegungen auf.
• Es können volumenelastische Verformungen auftreten. Sie erfordern
große Druckspannungen.
Modellvorstellung: Ideale Flüssigkeit
• Unter einer idealen Flüssigkeit versteht man eine inkompressible
Flüssigkeit ohne innere Reibung.
• An einer Oberfläche einer idealen ruhenden Flüssigkeit können keine
Tangentialkräfte auftreten. D.h. die Oberfläche einer idealen Flüssigkeit
steht immer senkrecht zu der auf die Flüssigkeit wirkenden Gesamtkraft.
1. Beispiel:
F = mg
Horizontale
Flüssigkeitsoberfläche in
einem ruhenden
Behälter
ω
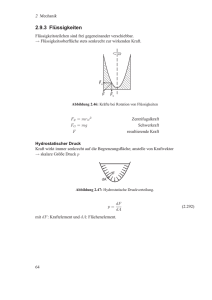
2. Beispiel
z
RotationsparaboloidOberfläche in einem
rotierenden Behälter
F1 = mg
r
F2
F2 = mω 2 x Zentrifugalkraft
r
F1
x
dz
= tan α
Steigung der Kurve:
dx
einsetzen: dz =
z ( x) =
ω2
g
ω x
∫ xdx =
2
g
ω2
2g
dx ⇒
r
F1
F2 mω 2 x
tan α =
=
F1
mg
dz
dxr
F
r
F2
x 2 + z 0 mit der Integrationskonstante für z (0) = z0
Druck in ruhenden Flüssigkeiten
Voraussetzungen:
• ideale Flüssigkeit
• Schwerkraft wird vernachlässigt
Bei ruhenden Flüssigkeiten treten nur Normalspannungen auf, die als
Druck bezeichnet werden.
r
F2
r
F3
r
F4
Erfahrung:
Es herrscht Gleichgewicht wenn
p1 =
F1 F2
=
= p2 ist.
A1 A2
Druckmessung im Inneren: p1 = p2 = p3 = p4
r
F1
Grundgesetz der Hydrostatik (Pascal-Gesetz):
Wenn man auf eine inkompressible, nicht der Schwerkraft unterworfene
Flüssigkeit an irgendeiner Stelle einen Druck ausübt, so herrscht überall an
der Gefäßwand und im Inneren der Flüssigkeit der gleiche Druck
(hydrostatischer Druck).
Begründung:
Wird der Kolben 1 ein Stück in das Gefäß hineinbewegt, wird der Kolben 2
ein Stück hinausgedrückt.
ΔV1 = ΔV2 ⇒ A1s1 = A2 s2
Dabei wird der Flüssigkeit keine Energie zugeführt oder entzogen:
W1 = W2 ⇒ s1F1 = s2 F 2
r
F2
Durch Division der Gleichungen folgt:
F1 F2
=
oder p1= p2
A1 A2
r
F1
Voraussetzungen:
• ideale Flüssigkeit
• Schwerkraft wird berücksichtigt
Kolben 1 wird ein Stück in das Gefäß hineingedrückt und Kolben 2 dadurch ein
Stück nach außen geschoben:
ΔV = A1 s1 = A2 s 2
r
F2
Das Flüssigkeitsvolumen ΔV wurde
dabei um die Strecke h angehoben.
Zugeführte Arbeit:
W = W1 − W2 = F1 s1 − F2 s 2
h
r
F1
W = mgh = ρΔV ⋅ gh = ρA1 s1 gh
Mit F1 = p1 A1 und F2 = p2 A2 und A1s1 = A2 s2 folgt:
p1 − p2 = ρgh
Die Formel p1 = p2 + ρgh gilt unabhängig von der Gefäßform.
Von der Oberfläche eines offenen Behälters aus gemessen
ergibt sich für den Druck in der Tiefe h: p ( h) = ρgh + p Luft
p Luft
h=0
h
Auftrieb
p1 = ρgh1 + p L ⇒ F1 = p1 A = ρgh1 A + p L A
r
F1
p2 = ρgh2 + p L ⇒ F2 = p2 A = ρgh2 A + p L A
h1
h2
h
FA = F2 − F1 = ρg ( h2 − h1 ) A ⇒
r
F2
FA = ρghA = ρgV = FG ( Flüssigkeit )
Fall 1: ρ ( Körper ) > ρ ( Flüssigkeit ) ⇒ Vρ K g > Vρ Fl g oder FG ( Körper ) > FA
Der Körper sinkt in der Flüssigkeit so weit wie möglich nach unten.
Fall 2: ρ ( Körper ) = ρ ( Flüssigkeit ) ⇒ Vρ K g = Vρ Fl g oder FG ( Körper ) = FA
Der Körper befindet sich in jeder Eintauchtiefe im Gleichgewicht, er schwebt
in der Flüssigkeit.
Fall 3: ρ ( Körper ) < ρ ( Flüssigkeit ) ⇒ FA > FG ( Körper ) (vollständi g eingetaucht )
Der Körper sinkt so tief in die Flüssigkeit ein, dass die Gewichtskraft des Körpers
und die Gewichtskraft der verdrängten Flüssigkeit denselben Betrag haben.
Der Körper schwimmt.
Schwimmen
stabile
Schwimmlage
instabile
Schwimmlage
Oberflächenspannung
1
1
2
r
Ebind (F1) < Ebind (2)
2
Definition der Oberflächenspannung
(spezifischen Oberflächenenergie) σ OF :
σ OF =
ΔW
ΔA
ΔA : Fläche um die die Oberfläche vergrößert wird.
ΔW : Arbeit, die notwendig ist, um die Oberfläche um ΔA zu vergrößern.
b
aufzuwendende Arbeit: ΔW = F ⋅ Δl
Oberflächenvergrößerung: ΔA = 2bΔl
l
Δl
Oberflächenspannung: σ OF =
r
F
ΔW FΔl
F
=
=
ΔA 2bΔl 2b
Druck in einer Seifenblase?
Gleichgewicht:
Durch die Oberflächenspannung erzeugter Druck = Überdruck in der Luftblase
Energiegewinn beim Verkleinern der Seifenblase:
W1 = 2 ⋅ σ OF ⋅ ΔA =
2σ OF {4π ( r + Δr ) 2 − 4πr 2 } =
r
2σ OF {8πrΔr + 4πΔr }⇒
2
W1 ≈ σ OF 16πrΔr
da Δr << rΔr
2
Gegen den Überdruck p geleistete Arbeit:
W2 = F ⋅ Δr = p ⋅ A ⋅ Δr = p ⋅ 4π (r + Δr ) 2 ⋅ Δr
W2 = p 4π (r 2 Δr + 2rΔr 2 + Δr 3 ) ⇒ W2 ≈ p ⋅ 4πr 2 ⋅ Δr
Gleichsetzen: W1 = W2 = σ OF 16πrΔr = p ⋅ 4πr ⋅ Δr ⇒
2
p=
4σ OF
r
Δr
Grenzfläche: Festkörper – Flüssigkeit
• Adhäsionskräfte
• Kohäsionskräfte
Fall 1: Adhäsionskräfte > Kohäsionskräfte
Æ Flüssigkeit benetzt den Festkörper
Fall 2: Adhäsionskräfte < Kohäsionskräfte
Æ Flüssigkeit benetzt den Festkörper nicht
Beispiele:
ϕ
ϕ
Glas – Wasser
Benetzung: ϕ < 90°
Quecksilber - Wasser
Nichtbenetzung: ϕ > 90°
r
F
Kapillarität
h
2σ OF
p=
r
r
2σ OF A
⇒ F=
r
Gleichgewicht: F = FG ⇒
2σ OF A
=ρV g=ρ Ahg
r
⇒ h=
2σ OF
rρ g
Die Kapillarität spielt bei vielen Alltagserscheinungen eine Rolle, z. B.:
• Kerzendochte
• Löschpapier
• Badeschwämmen
Bewegung idealer Flüssigkeiten
ΔV
v1
ΔV
A1
Δs1
v2
A2
Δ s2
Stromlinien: Anschauliche Darstellung der Strömung.
Linien, die an jeder Stelle die Richtung der momentanen Strömungsgeschwindigkeit
haben.
Stationäre Strömung: Der Stromlinienverlauf bleibt an jedem einzelnen Ort im
Laufe der Zeit unverändert.
Kontinuitätsgleichung und Bernoulli Gleichung
ΔV = Δs1 ⋅ A1 = Δs2 ⋅ A2
ΔV
v1
⇒ v1 ⋅ Δt ⋅ A1 = v2 ⋅ Δt ⋅ A2
⇒ v1 ⋅ A1 = v2 ⋅ A2
ΔV
v2
A1
A2
Δ s2
Δs1
Kontinuitätsgleichung
Die im Volumen ΔV befindliche Flüssigkeitsmenge der Masse Δm erfährt an
der Verengung einen Geschwindigkeitszuwachs Æ Zunahme von Ekin
1
ΔE kin = Δm(v22 − v12 )
2
F1 = p1 A1
W1 − W2 = F1Δs1 − F2 Δs 2
ΔW = p1 A1Δs1 − p 2 A2 Δs 2
F2 = p2 A2
ΔW = p1ΔV − p2 ΔV
mit ΔW = ΔE kin
1
1 Δm 2
⇒ ( p1 − p2 )ΔV = Δm(v22 − v12 ) ⇒ p1 − p 2 =
(v2 − v12 )
2
2 ΔV
1
1
⇒ p1 + ρv12 = p2 + ρv22 oder p + 1 ρv 2 = konstant Bernoulli Gleichung
2
2
2
Nicht horizontal verlaufende Strömungen:
1 2
p
+
ρ
gh
+
ρv = konstant
Allgemeine Bernoulli-Gleichung
2
Beispiel: Gesetz von Torricelli
1
h
2
1
1
p1 + ρgh1 + ρv12 = p 2 + ρgh2 + ρv22
2
2
1
p L + ρgh + 0 = p L + 0 + ρv 2
2
h=0
⇒ v = 2 gh
Beispiel: Stromlinienbild eines Flugzeugtragflügels
größere Geschwindigkeit Æ kleinerer Druck
kleinere Geschwindigkeit Æ größerer Druck
Reale Flüssigkeiten: Laminare Strömung
r
v
r
F
z
• untere Platte: in Ruhe
• obere Platte bewegt sich mit
konstanter Geschwindigkeit
v=0
Erfahrung: Kraft notwendig
η : dynamische Zähigkeit,
F ~v
F~A
1
F~
z
F =η ⋅ A
dynamische Viskosität oder
Koeffizient der inneren Reibung,
v
z
Einheit: 1Pa s = 1 N.s/m2.
1
η
: Fluidität
Beispiel: Stationäre horizontale Strömung mit innerer Reibung
p1
p2
2r
l
Zeitlich konstante Geschwindigkeitsverteilung: Kraft aufgrund der Druckdifferenz
Δp = p1 − p2 kompensiert die Reibungskräfte.
V A 2 ( p1 − p 2 ) πr 4 ( p1 − p 2 )
i= =
=
8πlη
8lη
t
i: Stromstärke
Beispiel: Versuch im Praktikum
2R
pL
h1
h2
h(t)
l
pL
p ( h) = p L + ρgh
dV π ⋅ r 4 Δp
=
i=
dt
8ηl
mit
Δp = p ( h) − p L = ρgh
π ⋅ r 4 ρgh(t )
⇒ i=
8ηl
dh
dh
= − AZ ⋅
Kontinuitätsgleichung: i = πR ⋅ v Z = −πR ⋅
dt
dt
dh
π ⋅ r 4 ρgh(t )
= − AZ ⋅
8ηl
dt
2
⇒
AZ 8ηl 1
t =−∫
⋅ dh ⇒
4
h1π ⋅ r ρg h
h2
2
AZ 8ηl h1 1
t=
dh
∫
4
π ⋅ r ρg h 2 h
η=
π ⋅ r 4 ρgt
⎛h ⎞
8 AZ l ln⎜⎜ 1 ⎟⎟
⎝ h2 ⎠