2.9.3 Flüssigkeiten

2 Mechanik
2.9.3 Flüssigkeiten
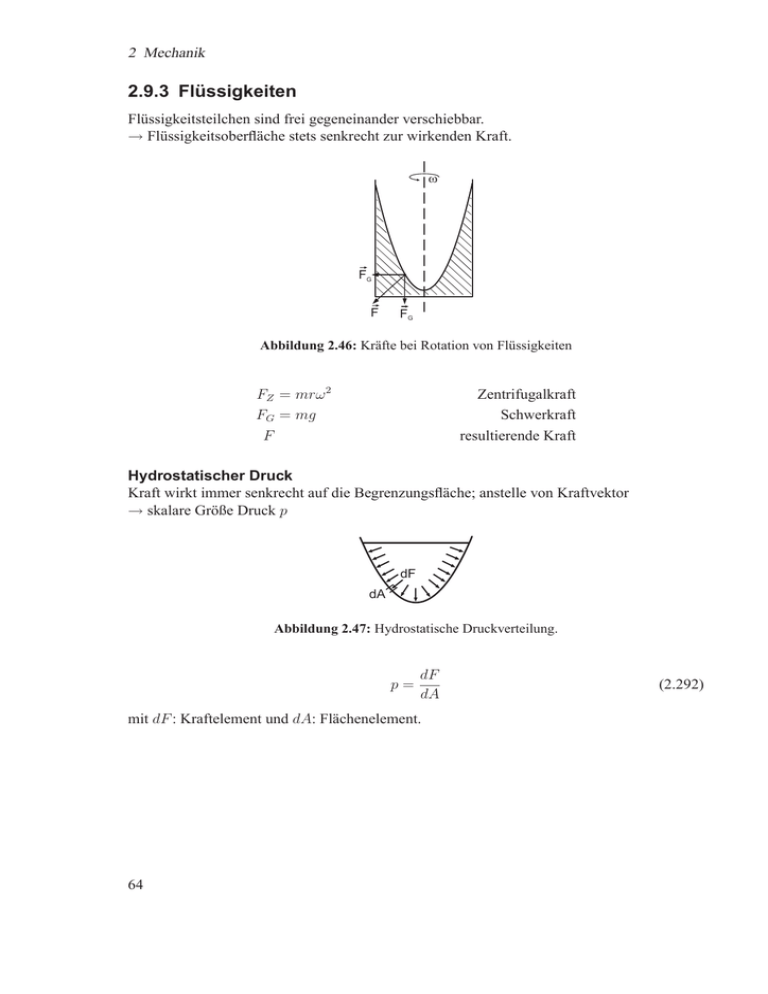
Flüssigkeitsteilchen sind frei gegeneinander verschiebbar.
→ Flüssigkeitsoberfläche stets senkrecht zur wirkenden Kraft.
w
FG
F
FG
Abbildung 2.46: Kräfte bei Rotation von Flüssigkeiten
FZ = mrω 2
FG = mg
F
Zentrifugalkraft
Schwerkraft
resultierende Kraft
Hydrostatischer Druck
Kraft wirkt immer senkrecht auf die Begrenzungsfläche; anstelle von Kraftvektor
→ skalare Größe Druck p
dF
dA
Abbildung 2.47: Hydrostatische Druckverteilung.
p=
dF
dA
mit dF : Kraftelement und dA: Flächenelement.
64
(2.292)
2.9 Mechanik deformierbarer Körper
Gesetz von Pascal
Überall im Inneren einer Flüssigkeit sowie an der Gefäßwand ist der Druck gleich.
Anwendung: Hydraulische Presse
F1
F2
A1
A2
Abbildung 2.48: Spart Kraft aber keine Arbeit.
F2
F1
=
A1
A2
A1
⇒ F1 =
F2
A2
p=
(2.293)
(2.294)
Schweredruck in Flüssigkeiten
Flüssigkeitssäule der Höhe h und der Querschnittsfläche A hat die Masse.
h
Abbildung 2.49: Schweredruck einer Flüssigkeitssäule.
m = ρhA;
⇒ F = gρhA;
F
= gρh;
⇒P =
A
ρ: Dichte
Kraft auf den Boden
(2.295)
(2.296)
Schweredruck einer Flüssigkeit
(2.297)
gρh
+
p0
+
pu
|{z}
|{z}
|{z}
Schweredruck offener Behälter, geschlossener
der Flüssigkeit
Luftdruck
Behälter,
der Umgebung
Kolbendruck
(2.298)
Gesamtdruck
p=
→ Quecksilberbarometer
65
2 Mechanik
→ kommunizierende Röhren: Zwei nicht mischbare Flüssigkeiten mit verschiedenen Dichten
H2O
Hg
Abbildung 2.50:
ρ1 und ρ2 stehen in den Schenkeln eines U-Rohrs.
p = gρ1 h1 = gρ2 h2
ρ1
h2
⇒
=
ρ2
h1
(2.299)
(2.300)
Auftrieb
Ein Körper taucht vollständig in eine Flüssigkeit ein. Der Auftrieb FA ist:
F1
h1
h2
F2
Abbildung 2.51: Auftriebskraft.
FA = F2 − F1 = gρ(h2 − h1 )A = gρV
(2.301)
Satz von Archimedes:
Der Auftrieb ist gerade so groß wie das Gewicht der verdrängten Flüssigkeitsmenge.
FA = FG ;
FA > FG ;
FA < FG ;
66
Körper schwebt in der Flüssigkeit
Körper schwimmt
Körper sinkt
(2.302a)
(2.302b)
(2.302c)
2.9 Mechanik deformierbarer Körper
(a)
(b)
(c)
FA
FA
S
M
S
SFL
FG
FA
S
M
SFL
SFL
FG
FG
Abbildung 2.52: Stabilität schwimmender Körper: (a) stabiles Schwimmen, (b) stabil aber schwankend
(c) labil. (S: Massenschwerpunkt, SFl : Schwerpunkt des verdrängten Volumens, M : Metazentrum)
Stabilitätsbedingung beim Schwimmen:
Der Angriffspunkt der Schwerkraft FG ist der Schwerpunkt S; der Angriffspunkt des Auftriebs
FA ist der Schwerpunkt SFl der verdrängten Flüssigkeit. Liegt S unterhalb von SFl so ist
~ = ~r × F~A
die Schwimmlage stabil. Liegt S oberhalb von SFl so wird ein Drehmoment M
erzeugt. Der Schnittpunkt der Mittelebene des Körpers mit der Wirkungslinie des Auftriebs
heißt Metazentrum M .
M oberhalb von S: Schwimmlage stabil
M unterhalb von S: Schwimmlage labil
2.9.4 Gase
Schweredruck
Bei einer Höhenzunahme dh ändert sich der hydrostatische Druck aufgrund der Abnahme der
darüberliegenden Gassäule.
dp = −ρgdh
ρ
p
für konstante Temperatur:
=
(Gesetz von Boyle-Mariott)
ρ0
p0
Z h
Z p
ρ0
dp
dh
=− g
⇒
p0 0
p0 p
p
ρ0 g
⇒ ln
=−
h
p0
p0
ρ0
⇒ p = p0 exp − gh (barometrische Höhenformel)
p0
(2.303)
(2.304)
(2.305)
(2.306)
(2.307)
67
2 Mechanik
2.9.5 Grenzflächeneffekte
Kohäsionskräfte:
Zwischen den Molekülen einer Phase (fest, flüssig, gasförmig) bestehen Anziehungskräfte
(Kohäsionskräfte)
Festkörper > Flüssigkeit > Gase
(2.308)
Adhäsionskräfte:
An einer Grenzfläche zwischen zwei verschiedenen Phasen auftretende zwischenmolekulare
Kräfte. Ursache der Benetzbarkeit von Oberflächen.
Oberflächenspannung:
Gas
Flüssigkeit
Fres
Fres=0
Abbildung 2.53: Oberflächenspannung.
Kohäsionskräfte heben sich im Inneren der Flüssigkeit auf, nicht aber an der Oberfläche.
⇒ Flüssigkeitsoberflächen sind Minimalflächen (energetisch günstigster Zustand).
σ=
dW
dA
(2.309)
Es wird auf die Arbeit dW zur Vergrößerung der Oberfläche dA verwendet.
Bestimmung der Oberflächenspannung:
F
ℓ
Ds
Abbildung 2.54: Messung der Oberflächenspannung.
σ=
F ∆s
F
dW
=
=
dA
∆s2l
2l
Die „2“ im Nenner taucht wegen Vorder- bzw. Rückseite des Drahtes auf.
68
(2.310)
2.9 Mechanik deformierbarer Körper
Grenzflächenspannung:
Festkörper - Flüssigkeit: σ12
Festkörper - Gas: σ13
Flüssigkeit - Gas: σ23
σ13 − σ12 = σ23 cos α
α ist der Kontaktwinkel
(a)
Flüssigkeit
~
s23 Gas
a
s12 s13
(b)
(2.311)
(c)
s23
s23
a
s12 s13
a
s12
s13
Festkörper
Abbildung 2.55: Grenzflächenspannung und Kontaktwinkel bei Benetzung und Tropfenbildung.
Kapilare Steighöhe:
Folge der Benetzbarkeit in engen Röhren mit dem Radius r:
a<90°
Dh
a>90°
Abbildung 2.56: Kapillareffekt in Röhren mit Radius r.
Gleichgewicht zwischen Oberflächenspannung und Gewichtskraft der angehobenen Flüssigkeitssäule:
F = σl = σ2πr
F = mg = ρV g = ρπr2 hg
gleichsetzen:
2σ
⇒h=
(vollständige Benetzung)
ρrg
2σ cos α
⇔h=
ρgr
(2.312)
(2.313)
(2.314)
(2.315)
69
2 Mechanik
70