Document
Werbung

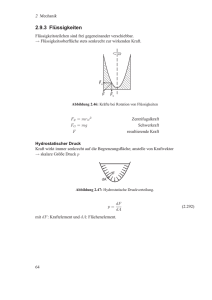
Vorlesung Physik für Pharmazeuten PPh - 05 Hydrostatik Grenzflächenspannung Hydrodynamik 21.05.2007 Ruhende Flüssigkeiten (Hydrostatik) Der hydrostatische Druck : F F P= A A [P]=N/m2 = Pa(scal) 1 bar=105 Pa Einfaches Druckmeßgerät (Manometer) Pascalsches Prinzip F Der Druck wirkt isotrop (in alle Raumrichtungen), unabhängig von der Gefäßform. Der Schweredruck FG = m ⋅ g m = ρ ⋅V = ρ ⋅ A ⋅ h h A Wo ist der hydrostatische Druck am größten? Hydrostatisches Paradoxon FG = ρ ⋅ g ⋅ A ⋅ h p = ρ ⋅g ⋅h Der Druck am Boden des Gefäßes ist unabhängig von der Form Versuch kommunizierende Röhren Hydraulische Presse (Anwendung des Pascalschen Prinzips) p1 = p2 F1 F2 = A1 A2 F1 ⋅s1 = F2 ⋅ s2 Energieerhaltung p1 ⋅ A1 ⋅ s1 = p1 ⋅ A2 ⋅ s2 Kolbenarbeit gegen den hydr. Druck W = p∆V Versuch Hydraulik Archimedisches Prinzip F1 = ρ ⋅g ⋅ h1 ⋅ A Fläche A FA = F2 − F1 = ρ ⋅ g ⋅ (h2 − h1 ) ⋅ A F2 = ρ ⋅ g⋅ h2 ⋅ A Schwimmen Schweben Sinken FA < FG FA = FG FA > FG FA = ρ ⋅ g ⋅V Auftriebskraft Ein Körper, der teilweise oder vollständig in eine Flüssigkeit eingetaucht ist, erfährt eine Auftriebskraft, deren Betrag gleich der Gewichtskraft der verdrängten Flüssigkeit ist Kompressibilität p1 V1 p2 V2 ∆V ∆p = −K ⋅ V ∆V = −κ ⋅ ∆p V K : Kompressionsmodul 1 κ= K Kompressibilität Festkörper und Flüssigkeiten sind inkompressibel (K ist groß) Der atmosphärische Schweredruck Formel für hydrostatischen Druck ∆p = −ρ ⋅ g⋅ ∆h Druck in bar 1.0 0.8 ∆h p0,ρ0 0.6 0.4 0.2 0 5 10 15 20 25 30 Höhe in km Barometrische Höhenformel p ρ = ρ0 p0 druckabhängige Dichte p ∆p = −ρ0 ⋅ g ⋅ ∆h p0 g ∆p = −ρ0 ⋅ p p0 ∆h ⎛ g ⎞ p(h) = p0 ⋅ exp ⎜⎜ − ρ 0 ⋅ h ⎟⎟ p0 ⎠ ⎝ Magdeburger Halbkugeln Nachweis des Luftdrucks durch Otto von Guericke (1602-1682) Versuch U-Rohr FlüssigkeitsManometer Torricellische Röhre zur Messung des Luftdrucks p = ρQuecksilber ⋅ g ⋅h ρQuecksilber = 13,6 kg / l Atmosphärischer „Normaldruck“: 1,013·105 Pa=1atm=1013mbar=760 Torr Wie hoch steht die Quecksilbersäule bei 1013 mbar? Kohäsionskräfte Flüssigkeiten im schwerelosen Raum suchen die Form mit der geringsten Oberfläche Quecksilbertropfen abgeflacht durch Schwerkraft Oberflächenspannung l F Oberflächenspannung =Kraft/Länge [N/m] F ~ σ= l Die Oberflächenspannung entspricht der Energie, die benötigt wird, um mehr Oberfläche einer Flüssigkeit zu erzeugen ~ ∆E = σ ⋅ ∆A Im Experiment (links) zählt Innen- und Außenfläche des Zylinders ∆A = 2 ⋅ 2π ⋅ r ⋅ ∆x also F = σ~ ⋅ 4π ⋅ r Tropfen & Oberflächenspannung R 2σ~ ∆P = R Kohäsionsdruck im Innern einer gekrümmten Flüssigkeitsoberfläche Abrisskriterium : ∆P ≈ FG / πR 2 Oberflächenspannung und Kontaktwinkel vollständig benetzend ϑ=0 gasf. (1) σ31 σ21 ϑ σ32 ϑ : Kontaktwinkel flüssig (2) fest (3) σ 31 = σ 32 + σ 21 ⋅ cos(ϑ ) ϑ partiell benetzend ϑ>0 Young-Dupre Gleichung Die Oberflächenspannung entspricht der Energie, die benötigt wird, um mehr Oberfläche einer Flüssigkeit zu erzeugen ~ ∆E = σ ⋅ ∆A Aero- & Hydrodynamik ∆V v1 Def. v2 dV I= = A⋅ v dt ∆V ⎡m3 ⎤ ⎢ ⎥ ⎣ s ⎦ v3 (Volumenstrom) Der Volumentransport einer stationären Strömung ist konstant. Kontinuitätsgleichung v1 ⋅ A1 = v 2 ⋅ A2 = v 3 ⋅ A3 = const Die ideale Flüssigkeit 1. keine Reibung 2. inkompressibel Die Summe aus stationärem Druck und Staudruck ist konstant 1 1 2 2 p1 + ρgh1 + ρ ⋅ v1 = p2 + ρgh2 + ρ ⋅ v 2 = const. 2 2 Bernoulli Gleichung Wenn die Strömungsgeschwindigkeit zunimmt fällt der Druck (Venturi-Effekt) Versuch: Strömungskanal Der Torricelli Becher Rechenbeispiel: Ausflußgeschwindigkeit einer Flüssigkeit v2 = v3, p2 = ?, h2=3,4 m v1 =0, p1 = patm, h1=2 m v3 = ?, p3 = patm, h3=0 m Die Flüssigkeit verlässt das Gefäß mit einer Geschwindigkeit, die dem freien Fall entspricht. Hydrodynamischer Effekt: Hohe Strömungsgeschwindigkeit erzeugt einen „Unterdruck“ Wasserstrahlpumpe Bunsenbrenner Versuch:Schwebender Ball Aerodynamik des Flugzeugflügels Die Differenz der Strömungsgeschwindigkeit an der Tragflächen Ober- und Unterseit führt nach der Bernoulli Gleichung zum Dynamischer Auftrieb Strömungswiderstand Strömung einer viskosen Flüssigkeit erfordert eine Druckdifferenz (treibende Kraft) ∆p = Rs ⋅ I Rs: Strömungswiderstand Serienschaltung Rges = R1 + R2 + R3 + ... 1. Kirchhoff‘sches Gesetz der Flüssigkeitsströmung Strömung durch Rohre L ∆r R : Radius p1 p2 Das Geschwindigkeitsprofil v(r) im Rohrist ein Rotationsparaboloid R4 I =π ∆p 8ηL ∆p 2 2 v(r ) = (R − r ) 4ηL Der Volumenstrom ist proportional zur Druckdifferenz Gesetz von Hagen-Poiseuille