12. Flüssigkeiten

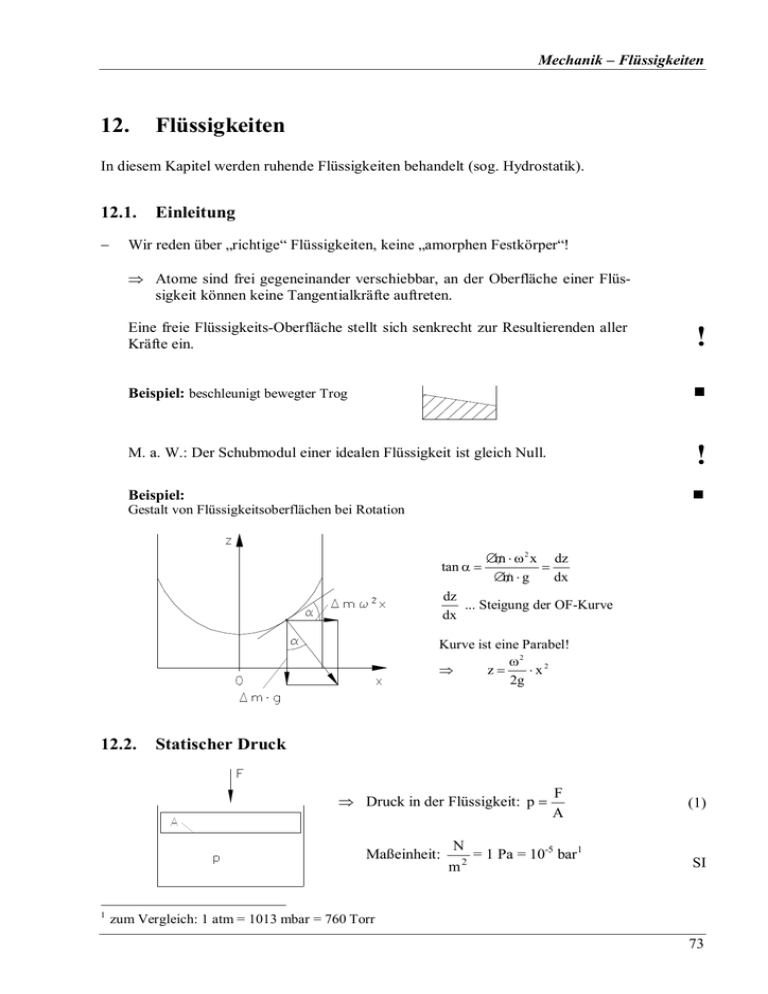
Mechanik – Flüssigkeiten
12.
Flüssigkeiten
In diesem Kapitel werden ruhende Flüssigkeiten behandelt (sog. Hydrostatik).
12.1.
−
Einleitung
Wir reden über „richtige“ Flüssigkeiten, keine „amorphen Festkörper“!
⇒ Atome sind frei gegeneinander verschiebbar, an der Oberfläche einer Flüssigkeit können keine Tangentialkräfte auftreten.
Eine freie Flüssigkeits-Oberfläche stellt sich senkrecht zur Resultierenden aller
Kräfte ein.
!
Beispiel: beschleunigt bewegter Trog
!
M. a. W.: Der Schubmodul einer idealen Flüssigkeit ist gleich Null.
Beispiel:
Gestalt von Flüssigkeitsoberflächen bei Rotation
tan α =
2
∆m
/ ⋅ ω x dz
=
dx
∆m
/ ⋅g
dz
... Steigung der OF-Kurve
dx
Kurve ist eine Parabel!
ω2 2
z=
⋅x
⇒
2g
12.2.
Statischer Druck
⇒ Druck in der Flüssigkeit: p =
Maßeinheit:
1
F
A
N
= 1 Pa = 10-5 bar1
2
m
(1)
SI
zum Vergleich: 1 atm = 1013 mbar = 760 Torr
73
Mechanik – Flüssigkeiten
−
Der Druck in einer Flüssigkeit ist allseitig, d.h. wirkt in alle Richtungen gleich.
−
Kompressibilität: in völliger Analogie zu Gl. (11 - 6) bildet man
1
1 dV
=− ⋅
K
V dp
κ ... Kompressibilität
K ... Kompressionsmodul
κ≡
!
(2)
Es zeigt sich, dass für fast alle Flüssigkeiten κ so klein bzw. K so groß ist, dass faktisch keine Komprimierbarkeit besteht. „Flüssigkeiten sind praktisch volumenstabil.“
−
!
hydraulische Presse, Heber, o.ä.:
Felsbrocken mit Masse M
⇒
⇒
p=
F1 = M ⋅ g
F1 M ⋅ g
=
A1
A1
wegen Allseitigkeit des Druckes muss nun auch gelten
⇒
p=
m⋅g
A2
m=
A2
⋅M
A1
Beispiel
1000 kg (Felsbrocken) ∧ A2/A1 = 1/1000 ⇒ Masse m = 1 kg hält die Waage!
−
Ist der Energiesatz verletzt?
Wir erhöhen m um ein sehr kleines ∆m, so dass sich der kleine Kolben um ∆h2
nach unten senkt.
⇒ geleistete Arbeit:
mit:
Win = ∆h 2 ⋅ F2
Win = ∆h 2 ⋅ A 2 ⋅ p
F2 = p ⋅ A 2
(1)
∆h 2 ⋅ A 2 = V ... Flüssigkeitsvolumen
74
Mechanik – Flüssigkeiten
Das Flüssigkeitsvolumen V strömt in den dicken Kolben und hebt diesen um ∆h1
gegen die Kraft F1:
⇒ am Fels geleistete Arbeit:
Wout = ∆h 1 ⋅ F1
F1 = p ⋅ A1
(1)
Wout = ∆h 1 ⋅ A 1 ⋅ p
Wobei wiederum
⇒
12.3.
−
∆h 1 ⋅ A1 = V ist.
Weil V in beiden Fällen gleich ist und p sowieso konstant, ist Win = Wout.
Hydraulik spart Kraft und braucht mehr Weg → Goldene Regel der Mechanik. Die Energie bleibt erhalten.
Schweredruck
Wir haben bis jetzt außer Acht gelassen, dass sich in einer Flüssigkeit ein
Schweredruck aufbaut:
Gewicht einer Flüssigkeitssäule (Querschnitt A, Höhe h, Dichte ρ)
FG = A ⋅ h ⋅ ρ ⋅ g
(3)
⇒ Schweredruck p(h):
p( h ) =
−
FG
= h ⋅ρ⋅g
A
(4)
Schweredruck nimmt mit der Tiefe zu und hängt nur von der Tiefe ab, sofern ρ
druckunabhängig ist, d.h. Inkompressibilität besteht.
Beispiel: Wasser ( ρ ≈ 10 3
kg
)
m3
1
≈ 5 ⋅ 10 −10 Pa −1
K
⇒ In 10.000 m Tiefe (bei 1000 atm) ist Dichte nur um 5% erhöht!
⇒ 1 bar ≈ 1 atm pro 10 m Tiefe, Kompressibilität κ =
−
Schweredruck und statischer Druck wirken zusammen. Oft ist einer der beiden
vernachlässigbar:
!
⋅ Meer (s.o.) ⇒ statischer Luftdruck vernachlässigbar
⋅ Hydraulikanlage ⇒ Schweredruck vernachlässigbar
−
hydrostatisches Paradoxon: „Der Bodendruck ist unabhängig von der Form des
Gefäßes.“ (nur abhängig von der Höhe!)
!
75
Mechanik – Flüssigkeiten
Alle diese Gefäße haben
gleichen Bodendruck!
Wenn wir die Gefäße unten verbinden (z.B. ein bereits gefülltes Verbindungsstück anfügen), wird sich wegen des einheitlichen Drucks in Bodennähe nichts ändern.
⇒ kommunizierende Gefäße haben gleiches Flüssigkeitsniveau!
Beispiele:
⋅ Wasserstandsanzeiger:
⋅ Schlauchwaage
12.4.
−
Auftrieb und Schwimmen
quaderförmiger Körper in einer Flüssigkeit, Höhe H, Grundfläche A:
Schweredruck der Flüssigkeit in der Tiefe h beträgt:
p = h ⋅ ρ Fl ⋅ g
⇒
auf obere Fläche wirkt Kraft
auf untere Fläche wirkt
(5)
F1 = h 1 ⋅ ρ Fl ⋅ g ⋅ A nach unten
F2 = h 2 ⋅ ρ Fl ⋅ g ⋅ A nach oben
In der Summe erfährt der Körper die Auftriebskraft FA
= Volumen V! (h1 - h2 = H)
FA = F2 − F1 = ρ Fl ⋅ g ⋅ A ⋅ (h 2 − h 1 )
FA = g ⋅ ρ Fl ⋅ V
Die Auftriebskraft entspricht dem Gewicht der verdrängten Flüssigkeitsmenge.
−
(6)
!
Die o.g. Herleitung ist zwar vereinfacht, Gl. (6) gilt aber für beliebig geformte Körper.
76
Mechanik – Flüssigkeiten
−
Das Verhalten des Körpers wird von FA + FG bestimmt:
!
FA < FG ⇒ Sinken; Körper ist schwerer
FA = FG ⇒ Körper schwebt
FA > FG ⇒ Körper schwimmt,
d.h. er taucht nur soweit ein, wie nötig ist, damit FA = FG ist:
Also:
Gewicht der verdrängten Wassermenge
= Gesamtgewicht des Schiffes
−
Stabilität:
Schwerpunkt S des Schiffes = Angriffspunkt der Schwerkraft
Schwerpunkt SF der verdrängten Flüssigkeit = Angriffspunkt der Auftriebskraft
⇒
12.5.
völlige Kentersicherheit nur, wenn S tiefer liegt als SF (schwerer Kiel); ansonsten existieren unterschiedliche kritische Kippwinkel
Oberflächenspannung
−
Experimente zeigen: Flüssigkeiten sind bestrebt, ihre Oberfläche klein zu halten
−
Deutung: ∃ gegenseitige Anziehung der Moleküle
der Flüssigkeit, wodurch diese zusammengehalten wird.
Moleküle an der Oberfläche erfahren resultierende
Kraft in die Flüssigkeit hinein → „Gummihaut“
2 Seiten einer Sache!
−
Energiedeutung: Ausbildung einer chemischen Bindung bedeutet Energieminimierung (Bindungsenergie wird frei!). Moleküle an der Oberfläche sind unvollständig
abgebunden ⇒ Oberfläche ist energetisch benachteiligt (∃ zusätzliche Wob)
⇒ Streben nach Minimierung der Oberfläche
−
Oberflächenenergie Wob ist proportional zur Oberfläche:
Wob = σ ⋅ A
Wob
A
σ ... spezifische Oberflächenenergie
σ
=





(7)
77
Mechanik – Flüssigkeiten
−
Maßein- [σ] = J
(Energie pro Fläche)
heit:
m2
SI
Die spezifische Oberflächenenergie heißt auch Oberflächenspannung.
!
Experiment: Aufspannen eines Flüssigkeitshäutchens mittels Drahtbügel:
Die mechanische Arbeit
∆W = F ⋅ ds
(8)
vergrößert die Oberflächenenergie um
∆Wob = σ ⋅ ∆A
∆A = 2 ⋅ b ⋅ ds
2 Oberflächen!
∆Wob = σ ⋅ 2 ⋅ b ⋅ ds
(9)
Gleichsetzung von (8), (9)
⇒
⇒
F ⋅ ds = σ ⋅ 2 ⋅ b ⋅ ds
F
=
σ
2b
(10)
Wir können σ also auch als Zugkraft pro Länge (in der Oberfläche), also als sogenannte Linienspannung auffassen:
Maßeinheit: [σ] =
−
N N⋅m
=
... (Kraft/Länge)
m
m2
J
= 2 ... (Energie/Fläche), also identisch zu Gl. (6)!
m
SI
Der Innendruck in einer Seifenblase:
Eine Verkleinerung des Radius um dr reduziert die Oberfläche OF einer Seifenblase um
dOF
⋅ dr
dr
dOF = 8πr dr
dOF =
(
)
d 4πr 2
= 8πr
dr
(11)
Die Seifenblase hat eine äußere und eine innere Oberfläche, daher ergibt das
dOF lt. Gl. (11) eine Reduzierung der Oberflächenenergie um
dWob = 16πr dr ⋅ σ
(12)
78
Mechanik – Flüssigkeiten
Bei r-Reduzierung muss aber gegen den Innendruck mechanische Arbeit geleistet werden:
dW = F ⋅ dr
F = Kugeloberfläche ⋅
Kraft
Kugeloberfläche
4πr 2
p
dW = 4πr ⋅ p ⋅ dr
2
(13)
Im Gleichgewicht haben sich r und p so eingestellt, dass dW = dWob ist.
⇒ Gleichsetzung von (12) und (13) liefert
p=
4σ
r
(14)
Kommentar:
p ist der in der Blase gegenüber der Umgebung herrschende Überdruck
p wächst mit zunehmendem σ und abnehmendem r!
Entsprechend Gl. (14) herrscht auch in jeder einfachen, nach außen mit Radius r gekrümmten Oberfläche ein Druck:
p=
12.6.
2σ
r
(15)
Fest-flüssig-Grenzflächen
12.6.1. Benetzung
−
Wir betrachten jetzt 3 Phasen:
Festkörper,
Flüssigkeit,
Gasphase (Luft + Dampf der Flüssigkeit + Dampf des Festkörpers).
Einstellen des Gleichgewichts an einer senkrechten Wand in einer Flüssigkeit bedeutet
Einstellung eines Randwinkels θ so, dass
σ ffl + σ fld ⋅ cos θ = σ fd
(16)
(YOUNGsche Gleichung)
−
Der gezeichnete Fall ist der der Benetzung (θ < 90° ≡ σfd > σffl)
79
Mechanik – Flüssigkeiten
−
andere Möglichkeit: Nichtbenetzung
(θ > 90° ≡ σfd < σffl)
−
Wenn nun selbst θ = 0 nicht reicht, um σfd zu kompensieren, gilt
σ fd > σ fld + σ ffl
Dann findet vollständige Benetzung statt, d. h. die Flüssigkeit kriecht als sehr
dünne Schicht ganz die Wand hoch; θ = 0°; σfd ist unendlich groß.
−
ähnlich beim Tropfen auf einer Oberfläche:
−
Benetzung ist wichtig!
Waschmittel (Reinigungswirkung)
Spülmittel („ohne abzutrockenen“)
Gefieder der Wasservögel
selbstreinigende Oberflächen






Benetzung
Nichtbenetzung
12.6.2. Kapillarität
−
In sehr dünnen Röhren steigen Flüssigkeiten höher als in ihrer Umgebung.
!
Zur Deutung nehmen wir vereinfachend
an, dass vollständige Benetzung vorliegt,
d.h. θ = 0° ist. (Ansonsten tritt dieser Effekt auch auf, aber nicht so ausgeprägt.)
−
verschiedene Deutungen möglich (mehrere Seiten derselben Medaille):
a) Die zusätzliche Flüssigkeitssäule mit
FG = πr 2 h ⋅ ρ ⋅ g
hängt an ihrer Randlinie (Länge 2πr) mit der Linienspannung σ fest.
⇒ Infolge dieser Spannung tritt eine „Haltekraft“ F auf:
F = 2πr ⋅ σ
80
Mechanik – Flüssigkeiten
Die Haltekraft kompensiert das Gewicht der zusätzlichen Flüssigkeitssäule:
πr 2 hρg = 2πrσ
2σ
h =
rρg
(17)
Also: Effekt umso größer, je größer σ ist und je kleiner r und ρ sind.
b) Der Schweredruck der Zusatzsäule ist
ps =
Gewichtskraft πr 2 hρg
=
= hρg
Grundfläche
πr 2
Er wird kompensiert durch den negativen Druck (d.h. Zug) der hier konkav
gewölbten Oberfläche lt. Gl. (15), also
2σ
= hρg
r
≡ Gl. (17)
Gl. (15)
c) Man erhält ebenfalls das gleiches Ergebnis, wenn man alle Energien betrachtet (Oberflächenenergien, Epot der Säule, usw.) und das Minimum sucht.
− Im nichtbenetzendem Fall (z.B. Glas/Hg) tritt Kapillardepression auf:
81