Parameteridentifikation

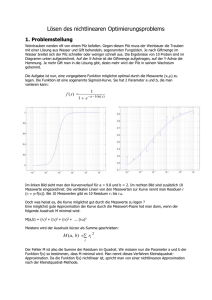
Parameteridentifikation
Grundsätzlich versucht man, die Koeffizienten der z-Übertragungsfunktion des Prozesses zu bestimmen (bei
einer Funktion n-ter Ordnung sind das 2n+1 Koeffizienten). Zur Bestimmung wird zumeist ein Digitalrechner
herangezogen, deshalb ist eine Diskretisierung des Prozesses notwendig - vorzugsweise mittels Abtast- und
Haltegliedern.
Im Digitalrechner wird nun ein Modell der Ordnung n erstellt, das zunächst unbekannte Koeffizienten hat. Diese
werden im Laufe der Parameteridentifikation so bestimmt, dass das Ausgangssignal des Modells mit dem
Ausgangssignal des Prozesses im störungsfreien Fall bei gleicher Erregung übereinstimmen würde. Die Störung
selbst wird dabei als eine Zahlenfolge modelliert, obwohl sie tatsächlich ein kontinuierliches Signal ist. Sie
bewirkt, dass auch bei perfekter Parameteridentifikation die Ausgangssignale von Modell und Prozess
unterschiedlich sind. Man geht jedoch davon aus, dass hier der Unterschied (nennen wir ihn Modellfehler)
minimal ist - eine Tatsache, die durch die Erfahrung gestützt wird, jedoch keineswegs eine logische
Notwendigkeit ist!
Direkt die Differenz der Ausgangssignale zu verwenden ist ungünstig, da hierbei die Fehlerfolge nichtlinear von
den Modellparametern abhängig ist. Man wählt deshalb einen anderen Ansatz für den Modellfehler:
TODO
Methode der kleinsten Quadrate
Man hofft, durch Minimierung der Fehlerenergie die Prozessparameter identifizieren zu können. Dazu
verwendet man die Ein- und Ausgangswerte der letzten N Abtastschritte und erhält damit die Messmatrix M:
  y n 1   y 0
 y
  y1
n
M : 
 


 y N 1   y N n
u0 
u1 
 

 u N n 
un 
u n 1 

uN
Diese ist eine schlanke Matrix mit N Zeilen und (2n+1) Spalten, wobei N >> n. Der Messfehler berechnet sich
nun zu:
e  y  M̂
Durch Nullsetzen der Ableitung des quadratischen Fehlers erhält man jene Modellparameter, bei denen der
Modellfehler minimal ist. Man geht nun davon aus, dass in diesem Fall die Modellparameter am besten mit den
Prozessparametern übereinstimmen:
̂  M T M  M T y  M  y
1
Dies trifft jedoch nur zu, wenn der Modellfehler ein weißes Rauschen ist. Das wiederum legt gewisse
Voraussetzungen für die Störfolge fest, die nun einem mit
1
A( z )
gefilterten weißen Rauschen entsprechen muss.
Grundsätzlich sollte man alle Kenntnisse über den Prozess bei der Parameteridentifikation mit einfließen lassen.
Weiß man also, ob ein System sprungfähig ist oder nicht, lässt sich unter Umständen bereits ein Parameter von
vornherein bestimmen.
Numerische Berechnung der Lösung
Man unterscheidet zwei verschiedene Möglichkeiten: die QR-Zerlegung und die Singulärwertzerlegung. Bei der
QR-Zerlegung wird die Massenmatrix in eine orthonormale Matrix Q (diese wird mithilfe des Gram-SchmidtVerfahrens bestimmt) und eine obere Dreiecksmatrix R zerlegt. Die Modellparameter ergeben sich zu:
M  QR  R̂  Q T y
Die Matrizeninversion kann man umgehen, da R eine obere Dreiecksmatrix ist, und man das Gleichungssystem
von unten nach oben fortschreitend auflösen kann.
Bei der Singulärwertzerlegung (SVD) wird die Messmatrix in das Produkt dreier Matrizen zerlegt, wobei die
mittlere der drei Matrizen eine Diagonalmatrix mit absteigend sortierten Singulärwerten (eine Art von
Eigenwerten) ist. Die Pseudo-Inverse der Massenmatrix, die zur Berechnung der Modellparameter herangezogen
wird, berechnet sich nun wie folgt:
M  UV T  M   V 1U T
Die SVD hat bessere numerische Eigenschaften als die QR-Zerlegung, mit ihrer Hilfe ist eine Datenreduktion
(Teile von U und V mit niedrigen Singulärwerten werden verworfen) mit Fehlerabschätzung möglich.
Rekursive Methode
Oft ist es notwendig, eine Parameteridentifikation im Betrieb vorzunehmen (On-Line-Identifikation), um den
Regler an die veränderte Strecke anpassen zu können. Bei der rekursiven Methode wächst die Messmatrix mit
jedem Abtastschritt um eine Zeile weiter. Mit der Messmatrix alleine zu rechnen, ist in diesem Fall also nicht
ratsam. Daher geht man darauf über, mehrere Rechenschritte gleichen Aufwands zu betreiben, und stattdessen
nur
M
T
N
MN

1
in jedem Schritt neu zu berechnen. Diese Matrix hat stets die Dimension (2n+1) x (2n+1).
Bei dieser Methode werden aber alle Werte der Vergangenheit mitberücksichtig, was nicht sinnvoll ist, da sich ja
das System verändert. Alte Werte können durch Fensterung oder exponentielle Gewichtung vernachlässigt
werden. Im einfachsten Fall betrachtet man zu jedem Zeitpunkt nur M zurückliegende Werte. Es sind zur
Bestimmung der Modellparameter in jedem Schritt nun zwar noch mehr Rechenoperationen nötig, diese besitzen
aber wieder konstanten Aufwand.
Diese Methode schafft es nicht nur, die neuen Modellparameter nach einer Änderung zu bestimmen, es ist sogar
eine Anpassung während der Änderung möglich. Die Breite des Fensters ist hier von großer Bedeutung: Je
schmäler das Fenster ist, desto leichter folgt das Modell einer Änderung, aber desto schlechter wird auch das
Einschwingverhalten.
Die Anforderungen an die Störungen sind dieselben wie bei der Methode der kleinsten Fehlerquadrate.
Identifikation durch Beschränkung der rekonstruierten Störgröße
Grundsätzlich ist zu sagen, dass wenn man die Modellparameter denen des Prozesses angepasst hat, man im
Modellfehler eine Rekonstruktion der Störgröße findet. Wenn nun z.B. die Störungen, die auf ein System wirken
ihrer Größe nach beschränkt sind, so gilt das auch für die rekonstruierten Störungen. Es lässt sich also ein
Identifikationsprozess entwickeln, bei dem man versucht, der rekonstruierten Störgröße gewisse Eigenschaften
aufzuprägen. Man kann nun also die Differenzengleichung für die rekonstruierte Störgröße aufstellen (in diesem
Fall für ein einfaches System erster Ordnung):
vˆk  aˆvˆk 1  yk  aˆyk 1  bˆuk 1
Durch Annahme einer Schranke ergeben sich für die Modellparameter und den Startwert der Störgröße
Ungleichungen, die zu erfüllen sind (die entspricht einem Bereich im 2n+1-dimensionalen Raum). Mit jedem
Abtastwert wird dieser Bereich aber eingeschränkt und er zieht sich immer weiter auf die wahren Werte
zusammen.
Zur Berechnung wird nun eine Zielfunktion eingeführt, die die Werte, um die die Störgröße die Schranke
überschreitet, für alle Abtastschritte zusammenzählt:
 v  M vk  M
mk   k
vk  M
 0
J (aˆ , bˆ, v0 )   mk
N
Diese Straffunktion wird nun mittels einer Optimierungsaufgabe minimiert und man erhält die Modellparameter.
Dabei ist die Wahl der Schranke von großer Bedeutung: Wählt man die Schranke zu groß, erhält man sehr
schnell ein Ergebnis, das von dem wahren Wert möglicherweise inakzeptabel weit entfernt liegt (die größere
Schranke resultiert in einem größeren Bereich um den wahren Wert). Wählt man die Schranke allerdings zu
klein, erhält man kein Ergebnis, weil die Optimierungsaufgabe nicht mehr lösbar ist (der Bereich verschwindet).
Alternativ dazu kann man die Zielfunktion derart wählen, dass die Schranke minimiert wird, dass also durch
Verändern der Modellparameter das Maximum der Störfolge minimal wird. In diesem Fall müssen die
Beschränkungen der Störgröße noch nicht einmal bekannt sein.
Das Verfahren ist toleranter gegenüber einer falsch gewählten Modellordnung, es benötigt jedoch erheblich mehr
Rechenzeit. Außerdem kommt man hier um ein Probieren nicht herum (vor allem, wenn man keine genauen
Informationen über die Störgröße besitzt). Auch eine On-Line-Identifikation ist mit dieser Methode möglich.
Formalismus von Lagrange
Die Berechnung der Bewegung eines Systems von Körpern mit Hilfe der Newtonschen Axiome
1. Es gibt Inertialsysteme, also Systeme, in denen der Impuls eines Körpers konstant ist.
2. An einen Körper angreifende Kräfte bewirken eine Impulsänderung.
3. Kraft und Gegenkraft sind gleich und entgegengesetzt gerichtet.
benötigt die Lösung eines Gleichungssystems. Zu diesem Gleichungssystem gehören neben den
Bewegungsgleichungen noch Zwangsbedingungen, die die Einschränkung der Bewegung beschreiben. Wir
betrachten nur holonome Zwangsbedingungen (diese lassen sich in Gleichungsform anschreiben; sind sie von
der Zeit direkt abhängig, heißen sie rheonom, andernfalls skleronom). Diese Zwangsbedingungen werden dann
als Zwangskräfte dargestellt, die zusätzlich zu den äußeren Kräften auf die Massenpunkte einwirken. N sei
hierbei die Anzahl der Massenpunkte, k die Anzahl der Zwangsgleichungen. Da die Zwangskräfte ebenso
unbekannt sind wie die gesuchten Ortskoordinaten, besteht das Gleichungssystem aus
3N  3k
Gleichungen. Macht man jedoch einen Ansatz für die Zwangskräfte, verringert sich die Anzahl der Gleichungen
folgendermaßen:
k



Z   l (t ) grad ri g l (r1 ,..., rN , t )
l 1
k
 
g
mi ri  Fi   l (t ) l
ri
l 1


g l (r1 ,..., rN , t )  0
Man nennt dies die Lagrange Gleichungen erster Art. Es lässt sich aber noch eine weitere Vereinfachung
machen. Betrachtet man nämlich die
n  3N  k
Freiheitsgrade des Systems von Massenpunkten, kann man leicht n generalisierte Koordinaten q einführen, die
einerseits die Lage aller Massenpunkte eindeutig bestimmen müssen, und andererseits selbst keinen
Beschränkungen unterliegen dürfen (d.h. sie erfüllen die Zwangsbedingungen in jedem Fall). Es zeigt sich, dass
sich die Zwangskräfte damit auslöschen. Die an die Körper angreifenden Kräfte müssen nun jedoch auf die
generalisierten Koordinaten projiziert werden, man spricht dann von generalisierten Kräften. Durch
Umformungen gelangt man schließlich zu den Lagrange Gleichungen zweiter Art, also zu einem System von
gewöhnlichen Differentialgleichungen zweiter Ordnung (sie sind zwar nichtlinear, dennoch oft leichter zu lösen
als das Gleichungssystem, das mit den Newtonschen Axiomen aufgestellt wurde). Diese stellen die minimale
Anzahl von Gleichungen dar; nachteilig ist jedoch, dass man die Ortskoordinaten der Massenpunkte nicht mehr
direkt erhält und auch eine Berechnung der Zwangskräfte nicht mehr möglich ist. Durch die Ableitung
N
T 
i 1
mi  2
ri
2
d  T
dt  q j
 T

 Qj
 q
j

T  T q j , q j , t 
T
 h j q j , q j , t 
q j
T
 f j q j , q j , t 
q j
d  T
dt  q j
 T f j
f j
f


q1  ... 
q1  ... 
 hj  Qj
 q
q1
q1
t
j

Mq  Dq  r  
ist ersichtlich, dass es tatsächlich gewöhnliche Differentialgleichungen sind. Diese lassen sich in ein System von
Differentialgleichungen erster Ordnung überführen:
Mq  Dq  r  
q  v
v
q  

 v    M 1 Dv  M 1r  M 1 
  

Die Lagrange Gleichungen lassen sich sogar noch weiter vereinfachen, wenn man weiß, dass einige der äußeren
Kräfte von Potentialen resultieren. Diese Potentiale können entweder konservativ (nur von der Position und der
Zeit abhängig) sein, wie z.B. das Federpotential und das Gravitationspotential, oder sie können verallgemeinert
sein (von der Position, der Zeit und der Geschwindigkeit abhängig) sein, wie z.B. das magnetische Potential.
Zieht man die Potentiale V von der kinetischen Energie T ab, erhält man die Lagrange-Funktion L. Schließlich
kann man mithilfe der Dissipationsfunktion P noch die dissipativen Kräfte (Reibungsverluste, ohmsche Verluste
in mechatronischen Systemen) berücksichtigen. Da diese Kräfte zumeist von der Geschwindigkeit abhängig
sind, müssen sie auf die zeitlichen Ableitungen der generalisierten Koordinaten projiziert werden. Man erhält als
letzte Vereinfachung der Lagrange Gleichungen zweiter Art:
L  T V
d  L
dt  q j
 L
P


 Qj
 q


q
j
j

Anwendung auf mechatronische Systeme
Man kann in elektrischen Schaltungen als generalisierte Koordinate die Ladung wählen. Die kinetische Energie
ist dann jene Energie, die in der Spule gespeichert wird. Der Impuls ist durch die Flussverkettung, das Potential
durch Kondensatoren vorgegeben. Die generalisierte Kraft ist eine Spannungsquelle. Wählt man hingegen den
Fluss als generalisierte Koordinate, wird die Energie im Kondensator, das Potential in der Spule und die
generalisierte Kraft in der Stromquelle begründet.
Die Spannung ist die zeitliche Ableitung des Flusses, der Strom jene der Ladung. Würde man diese üblichen
Variablen verwenden, würden die Netzwerke durch Integro-Differentialgleichungen beschrieben.
Numerische Lösung gewöhnlicher Differentialgleichungen
Grundsätzlich muss bei einer numerischen Lösung einer Differentialgleichung diese zuerst diskretisiert werden.
Man unterscheidet Verfahren mit konstanter und Verfahren mit variabler Schrittweite. Letztere stellen sich als
sinnvoller heraus, um den Rechenaufwand (und damit die Rundungsfehler) zu minimieren: In Bereichen großer
Dynamik wählt man kleine Schrittweiten, in Bereichen kleiner Dynamik hingegen große Schrittweiten.
Grundsätzlich gibt es zwei Ansätze für Algorithmen: Die Taylorreihe und die Polynomapproximation. Bei der
Taylor-Reihe verwendet man lediglich die Information der letzten Stützstelle, um den Ort der folgenden
Stützstelle zu berechnen; man setzt sie daher bei Einschrittverfahren ein. Bei der Polynomapproximation
hingegen verwendet man die letzten k Stützstellen, um ein Polynom aufzustellen, das man dann zur nächsten
Stützstelle extrapoliert. Diese Mehrschrittverfahren benötigen viele Startwerte, die oft mit Einschrittverfahren
berechnet werden. Dafür sind sie genauer.
Grundsätzlich unterscheidet man zwischen lokalen Fehler und globalen Fehlern. Lokale Fehler entstehen unter
der Voraussetzung, dass die bisher berechneten Werte korrekt waren; sie akkumulieren sich im Laufe der
Berechnung aber zu globalen Fehlern. Die Fehler werden weiter in Diskretisierungsfehler und Rundungsfehler
unterteilt. Diskretisierungsfehler entstehen aus dem Algorithmus: Sowohl bei der Taylor-Reihe als auch bei der
Polynomextrapolation wird der Fehler umso größer, je größer die Schrittweite ist. Rundungsfehler hingegen
entstehen aus dem endlichen Zahlenformat des Rechners: Je mehr Rechenoperationen notwendig sind, desto
größer ist also der Rundungsfehler - der Rundungsfehler sinkt mit steigender Schrittweite. Es gibt also für jede
Differentialgleichung bei gewähltem Zahlenformat und gewähltem Algorithmus eine unbekannte, optimale
Schrittweite.
Einschrittverfahren
Das Euler-Verfahren entspricht einer Taylor-Entwicklung erster Ordnung: An der alten Stützstelle wird die
Tangente angelegt und man wandert auf dieser um eine Schrittweite weiter. Euler-Verfahren besitzen große
globale Fehler. Verbesserungen bieten die Runge-Kutta-Verfahren. Wir diskutierten hier zwei Verfahren zweiter
Ordnung, nämlich den Heun-Algorithmus und den modifizierten Euler. Bei Verfahren höherer Ordnung wird die
Ableitung der rechten Seite durch mehrfaches Auswerten derselben umgangen.
Der Heun-Algorithmus z.B. macht einen Euler-Schritt (Prädiktorschritt) und ermittelt an der neuen Stützstelle
die Steigung. Dann führt er einen Korrektorschritt aus, indem mit einem Mittelwert aus der Steigung von alter
und im Euler-Schritt ermittelter Stützstelle die neue Stützstelle berechnet.
Der modifizierte Euler macht einen halben Euler-Schritt und verwendet die Steigung an diesem Punkt, um von
der alten Stützstelle ausgehen die neue zu berechnen.
Mehrschrittverfahren
Bei Mehrschrittverfahren interpoliert man die vergangenen Stützstellen zu einem Polynom und extrapoliert es
um einen Schritt. Man hat hier Einfluss auf zwei Parameter: Die Anzahl der zurückliegenen Schritte und den
Grad des Interpolationspolynoms. Die Ableitung zeigt, dass es sinnvoll ist, Stützstellenanzahl und Polynomgrad
gleich zu wählen und zudem noch ein Polynom gerader Ordnung anzustreben (die Zahl der Stützstellen ist damit
ungerade): Bei dieser Wahl ist der Fehler nämlich von der Ordnung r+2, wobei das Polynom den Grad r-1 hat.
Implizite Verfahren verwenden bei der Berechnung des Polynoms auch zunächst unbekannte Funktionswerte
(nämlich jene, die in diesem Schritt zu berechnen wären). Diese Funktionswerte werden dann zuerst mittels
expliziter Verfahren oder mittels eines Euler-Schrittes geschätzt.
Stabilität
Ein Algorithmus ist absolut stabil, wenn die numerische Lösung des Testproblems abklingt, sofern auch die
analytische Lösung abklingt. Um das Gebiet absoluter Stabilität zu untersuchen, betrachten wir eine
Exponentialfunktion, deren Differentialgleichung und die z-Transformation der Differentialgleichung. Wir
erhalten also das Gebiet absoluter Stabilität für Euler-Verfahren:
y  e x  y '   y
yi 1  yi  hf ( xi , yi )  yi  hyi  yi 1  h 
z  y ( z )  y0   y ( z )1  h 
y ( z ) z  1  h   zy0
zy0
z  1  h
i
yi  1  h  y0
y( z) 
stabil für : 1  h  1
Es lässt sich zeigen, dass Runge-Kutta-Verfahren höherer Ordnung keine wesentliche Vergrößerung des
Stabilitätsgebietes mit sich bringen.
Die Untersuchung zeigt, dass die Schrittweite durch die Eigenwerte eines Systems, genauer: durch den größten
Eigenwert des Systems, vorgegeben wird. Bei mechatronischen Systemen liegen die Eigenwerte aber oft in ganz
unterschiedlichen Bereichen: Die elektrischen Eigenwerte sind groß (schnelles Abklingverhalten, große
Dynamik), die mechanischen hingegen klein (träge Massen). Während also die elektrischen Eigenwerte die
Schrittweite klein halten, interessieren uns aber oft die mechanischen Auswirkungen - das erfordert lange
Simulationszeiten. Systeme, in denen das Verhältnis zwischen dem größten und dem kleinsten Eigenwert größer
als 1000 ist, nennt man steife Systeme. Diese werden durch eigene Algorithmen (stif-Algorithmen, GearAlgorithmus) behandelt; diese Algorithmen haben aber den Nachteil, dass sie für kombinierte diskrete und
kontinuierliche Systeme nicht gut geeignet sind.
Schrittweitensteuerung
Grundsätzlich steuert man die Schrittweite abhängig vom Diskretisierungsfehler. Diesen berechnet man, indem
man die neue Stützstelle zweimal berechnet, beim zweiten Mal aber mit einem höherwertigeren Verfahren. Beim
Heun-Algorithmus wird z.B. die Stützstelle im zweiten Durchgang mit korrigierter Steigung berechnet. Beim
Verfahren Runge-Kutta-23 wird hingegen im ersten Durchlauf mit einem modifizierten Euler die Stützstelle
berechnet, und durch eine einzige zusätzliche Auswertung der rechten Seite erhält man die Stützstelle, wie sie
ein Verfahren dritter Ordnung berechnet hätte. Die Differenz der beiden Werte, bezogen auf den genaueren
Wert, nennt man Diskretisierungsfehler. Über- bzw. unterschreitet er eine bestimmte Grenze, wird die
Schrittweite verkleinter bzw. vergrößert.