Stahlbetonformeln: Leitfaden für den konstruktiven Ingenieurbau
Werbung
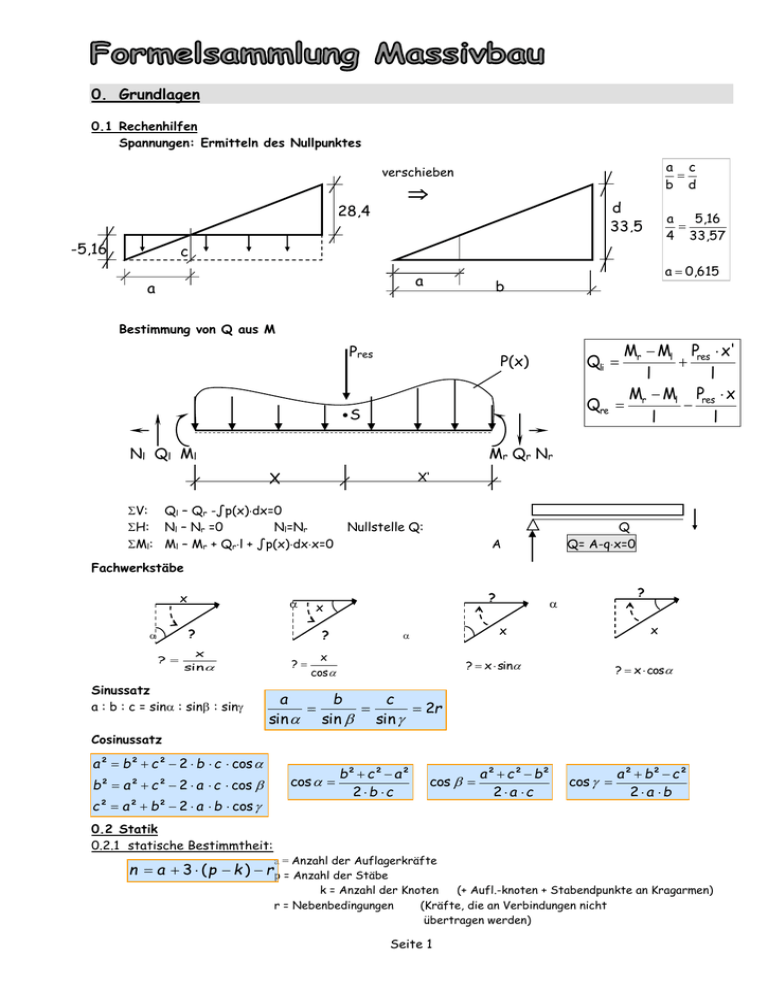
0. Grundlagen 0.1 Rechenhilfen Spannungen: Ermitteln des Nullpunktes a c b d verschieben 28,4 1 -5,16 d 33,5 7 c a a a 5,16 4 33,57 a 0,615 b Bestimmung von Q aus M Pres Mr Ml Pres x' l l M Ml Pres x Qre r l l Qli P(x) S Nl Ql Ml Mr Qr Nr X X‘ V: Ql – Qr -∫p(x)dx=0 H: Nl – Nr =0 Nl=Nr Ml: Ml – Mr + Qrl + ∫p(x)dxx=0 Nullstelle Q: Q Q= A-qx=0 A Fachwerkstäbe x ? ? ? x sin Sinussatz a : b : c = sin : sin : sin ? x ? ? x x x cos ? x sin ? x cos a b c 2r sin sin sin Cosinussatz a² b² c² 2 b c cos b² a² c² 2 a c cos c² a² b² 2 a b cos 0.2 Statik 0.2.1 statische Bestimmtheit: cos b² c² a² 2b c cos a² c² b² 2 a c cos a² b² c² 2a b a = Anzahl der Auflagerkräfte n a 3 ( p k ) r p = Anzahl der Stäbe k = Anzahl der Knoten (+ Aufl.-knoten + Stabendpunkte an Kragarmen) r = Nebenbedingungen (Kräfte, die an Verbindungen nicht übertragen werden) Seite 1 N mm² N cm² kN mm² kN cm² kN m² MN cm² MN m² 1 N/mm² = 1 102 10-3 10-1 103 10-4 1 1 N/cm² = 10-2 1 10-5 10-3 10 10-5 10-2 1 kN/mm² = 103 105 1 102 106 10-1 103 1 kN/cm² = 10 103 10-2 1 104 10-3 10 1 kN/m² = 10-3 10-1 10-6 10-4 1 10-7 10-3 1 MN/cm² = 104 106 10 103 107 1 104 1 MN/m² = 1 102 10-3 10-1 103 10-4 1 Einheiten 0.3 Begriffe Druckbewehrung Bei zunehmender Beanspruchung eines Querschnitts ist es erforderlich, entweder eine Umschnürungsbewehrung einzubauen oder die bezogene Druckzonenhöhe zu begrenzen um ein duktiles Tragverhalten (hohe Rotationsfähigkeit) zu gewährleisten. Um diese Begrenzung einhalten zu können ist es ggf. erforderlich eine Druckbewehrung anzuordnen. Auswirkung: zunehmende Beanspruchung Bei zunehmender Beanspruchung steigt die aufzunehmende Druckkraft im Beton. Werden die Betonspannungen ausgenutzt, ist die Vergrößerung der Betondruckkraft nur über eine Vergrößerung der Betondruckzone möglich, was eine Verschiebung der Dehnungsnulllinie nach unten bewirkt. Durch diese Verschiebung verringert sich auch die Stahldehnung. Sinkt die Stahldehnung unter die Dehnung an der Streckgrenze, wird die Zugbewehrung nicht mehr voll ausgenutzt, was einen unwirtschaftlichen Querschnitt zur Folge hat. Zudem bewirkt die erhöhte Ausnutzung der Biegedruckzone eine Reduzierung der Duktilität. Dies führt zu einer maßgebenden Versagensursache durch s chlagartiges Versagen der Biegedruckzone anstatt des Fließens der Zugbewehrung. 1. Grundlagen Sicherheitstheorie 1.1 Grenzzustände Grenzzustand der Tragfähigkeit Sd Rd (Biegung mit Längskraft, Querkraft und /oder Torsion, Durchstanzen, Stabilitätsversagen, Dauerschwingbeanspruchung) Sk Rk = charakteristische Einwirkung = charakteristischer Widerstand Sd Rd = Bemessungswert der Beanspruchung aus einer, oder einer Kombination von Einwirkungen = Bemessungswert der Beanspruchbarkeit (Baustoffwiderstand) Grenzzustand der Gebrauchstauglichkeit (Begrenzung der : Rissbreite, Spannungen und Verformungen) Es wird mit charakteristischen Werten gerechnet d.h. ist in der Regel =1 Einwirkungen Nur Kombinationsbeiwert (bei mehr als einer Einwirkung) Ed C d oder Ed Rd Ed Cd Rd = Bemessungswert der Lastauswirkung (z.B. Durchbiegung) = Maßgebender / einzuhaltender Nennwert (z.B. Grenzwert der D) = Bemessungswert des Tragwiderstandes 2.0 Bemessungswerte zur Sicherheitstheorie 2.1 Bemessungswerte der Baustoffeigenschaften: fyk f Rd R ck , c s = = Abminderungsbeiwert zur berücksichtigung der verminderten Dauerstandfestigkeit gegenüber der Kurzzeitfestigkeit 0,85 Normalbeton (Schneider (neu) S. 5.31) 0,75 Leichtbeton (0,70 bei rechteckigem Spannungsblock) Seite 2 M = Teilsicherheitsbeiwert der Widerstandsgrößen Zur Berechnung der Bemessungswerte der Steifigkeiten und Festigkeiten im Tragsicherheitsnachweis. (DIN 1045-1, Tab. 2, S. 24) Beton c C12/15 bis C55/67 bis C50/60 C100/115 Unbewehreter Beton Grundkombination Außergewöhnliche Kombination (ausgenommen Erdbeben) Nachweis der Ermüdung 1,5 1,8 1,5 1,55 1,3 1,3 - 1,5 1,5 Betonstahl s 1 fck 500 1,1 1,15 1 1,1 1,0 fck 500 1 1,1 1,15 fck 500 Tab.2.1 Teilsicherheitsbeiwerte M für die Bestimmung des Tragwiderstandes (MI-Skript, S.4.10) 2.2 Bemessungswerte der Einwirkungen: Gk,i = charakteristische ständige Einwirkung Qk,i = charakteristische veränderliche Einwirkung Ak,i = charakteristische außergewöhnliche Einwirkung AE = seismische Einwirkunegen = Teilsicherheitsbeiwert der Einwirkungen = Kombinationsbeiwert 2.2.1 Einwirkungen im Grenzzustand der Tragfähigkeit I. ständige und vorübergehende Bemessungssituation Ed ( j G, j Gk, j ) Q,l Qk,1 ( i l 0,i Q,i Qk,i ) II. Außergewöhnliche Bemessungssituation Ed ( j GA, j Gk, j ) Ad 1,l Qk,1 ( i l 2,i Qk,i ) Ad = Bemessungswert (festgelegter Wert) der außergewöhnlichen Belastung 2.2.2 Einwirkungen im Grenzzustand der Gebrauchstauglichkeit I. seltene (charakteristische) Kombination G Ed, rare E Qk,1 0,i Qk,i k, j II. Nicht-häufige Kombination G Ed,inf r E k, j '1,1 Qk,1 1,i Qk,i III. Häufige Kombination G Ed, f requ E k, j 1,1 Qk,1 2,i Qk,i IV. Quai-ständige Kombination (bei Rissbreitenbegrenzung) G Ed, perm E k, j 2,i Qk,i Ständige Einwirkungen G GA Veränderliche Einwirkungen Q Günstige Auswirkung 1,00 1,00 0 Ungünstige Auswirkung 1,35 1,00 1,5 Tab. 2.2 Teilsicherheitsbeiwerte F für Einwirkungen (MI-Skript, S. 4.10) Seite 3 Einwirkung 0 Nutzlasten für Hochbauten: Kategorie A, B: Wohn- und Aufenthalts-, Büroräume Kategorie C, D: Versammlungsräume, Verkaufsräume Kategorie E: Lagerräume Verkehrslasten für Hochbauten: Kategorie F: Fahrzeuggewicht 30 kN Kategorie G: 30 kN Fahrzeug 160 kN Kategorie H: Dächer Windlasten Schnee- und Eislasten Orte bis zu NN +1000 Orte über NN +1000 Temperatureinwirkungen (nicht Brand) Baugrundsetzungen Alle anderen Einwirkungen Kombinationsbeiwert 1 2 0,7 0,7 1,0 0,5 0,7 0,9 0,3 0,6 0,8 0,7 0,7 0 0,6 0,5 0,7 0,6 1,0 0,8 0,7 0,5 0 0,5 0,2 0,5 0,5 1,0 0,7 0,6 0,3 0 0 0 0,2 0 1,0 0,5 Nutzlasten mehrgeschossige Hochbauten in 1055-3 Ggf. Abänderungen für unterschiedliche geogr. Gegenden unabh. Einwirkungen wie Erd- oder Wasserdruck werden in DIN 1055-100 behandelt oder sind standortbedingt festzulegen Beiwerte für Maschinenlasten sind betriebsbedingt festzulegen Tab.2.3 Kombinationsbeiwerte der Einwirkungen (MI-Skript, S.4.9) Seite 4 3. Geometrie 3.1 effektive Auflagerbreite nicht durchlaufend durchlaufend volle Einspnnung h h t t leff leff ln ln leff ln t ai 1 2 t 1 ta 1 t i 3 2 freier Kragträger Kragarm Durchlaufträger t h leff ln 1 2 t ai 12 h h leff ln ai 1 2 t leff ln a1 a2 Seite 5 4. Betondeckung 4.1 Expositionsklasse bestimmen: Bewehrungskorrosion maßgeblich für cmin und ∆c Betonkorrosion Der größere Wert (CXX/YY) ist maßgeblich für die Betonfestigkeit 4.2 Mindestbetondeckung ermitteln: cmin Betondeckung c cnom Anmerkung Längsbewehrung z.B. Korrosionsschutz Bügelbewehrung z.B. Verbundsicherung Tab. 4.1 Ermittlung der Mindestbetondeckung Aus der Tabelle kann das Verlegemaß nach folgender Formel ermittelt werden cnom,bü cv cnom,l dsbü 4.3 Vorschätzen der Bewehrungsdurchmesser: Längsbewehrung (dsl): Ø 20-25 Bügelbewehrung: Ø 10-17 4.4 Mindestbetondeckung prüfen: 1. Nachweis Sofortiger Verbund Nachträglicher Verbund cmin cmin cmin cmin cmin ≥ dsbü (für Bügel) ≥ dsv (für Matten und Stahlbündel) ≥ 2,5 * dlitze (für Litzen) ≥ 2,5 * dger-Stahl (für gerippten Stahl) ≥ dhüllrohr (für Hüllrohre) cmin + dsbü ≥ dsl 2. Nachweis (dsl Längsbewehrung) 4.5 Bestimmen von cnom: cnom = cmin + ∆c Das Nennmaß cnom wird sowohl für die Bügel als auch für die Längsbewehrung ermittelt. 4.6 Berechnen der statischen Höhe: d h cnom d sb d sl 2 bei mehreren Lagen (z.B. Plattenbalken) = Lagen + Zwischenräume Erläuterung: dsl (Längsstab) dsbü (Bügel) cv (Verlegmaß) cnom,bü cnom,l Seite 6 5. Balken auf zwei Stützen 5.0 Allgemeines 1) leff 2) fyd / fcd 3) maßgebliche Streckenbelastung gd und qd Einzellasten G oder Q (günstig/ungünstig) 4) d bestimmen 5) Schnittkräfte bestimmen 6) Momentenausrundung für Zwischenauflager 7) Momentenumlagerungen im Feld (falls ausdrücklich verlangt) 5.1 statisches System Für den Balken wird zunächst ein statisches System gewählt und die wirksame Stützweite l eff ermittelt. (Siehe dazu 2.xx) 5.2 Schnittgrößen Ermittlung der aus den Einwirkungen entstehenden Zustandslinien. 5.3 Biegung und Längskraft (Tragfähigkeit) 5.3.1 Querschnitte mit rechteckiger Druckzone Für die Bemessung werden die auf die Schwereachse bezogenen Schnittgrößen ind versetzte Schnittgrößen umgewandelt. Neue Bezugslinie ist hier die Achse der Biegezugbewehrung. h d zs2 zs1 As2 MEd NEd As1 MEds = MEd – NEd zs1 NEd =NEd Die Betonzugzone wird als gerissen angenommen und darf bei der Bemessung nicht in Rechnung gestellt werden. Die Lage der Betondruckzone muss falls vorgewählt nachgewiesen werden! (über: x = d) Der Tragfähigkeitsnachweis erfolgt mit Hilfe von Identitätsbeziehungen d.h., dass die einwirkenden Schnittgrößen NEd und MEds identisch mit den Widerständen NRd und MRds sein müssen. NEd NRd und MEds = MEd - NEd zs MRds Die Bemessung kann nun “per Hand” (im Allgemeinen iterativ) erfolgen oder mit Hilfe von Bemessungstafeln. Bemessung per Hand (durch die Annahme eines Stoffgesetzes) Bei der Ermittlung per Hand gelten die folgenden Gleichungen zur Ermittlung der „inneren“ Schnittgrößen bzw. Widerstände. 0N Fcd Fs 2d Fs 1d mit Fcd x b R fcd Rd MRsd Fcd z Fs 2d (d d2 ) Fs 2d As 2 s 2d Fs 1d As 1 s 1d Seite 7 Die Hilfsgrößen setzten sich wie folgt zusammen: a = kax x=d z=d R mit Randabstand der Betondruckkraft; ka nach Tafel 1 (für Normalbeton bis C50/60) Höhe der Druckzone; Hebelarm der inneren Kräfte Völligkeitsbeiwert; R nach Tafel 1 (für Normalbeton bis C50/60) c 2 c2 1 s1 a d Tafel 1 Hilfswerte ka und v für C12/15 bis C50/60 0 0 00 c 2 2,0 0 (MI-Skript, Bild 5.7, S. 5.10) 00 4 6 c 2 c 2 3 c 2 4 2 2 c 2 3 c 2 2 c 2 6 c 2 3 c 2 2 8 c2 ka R 2 0 00 c 2 3,5 0 00 3 c 2 12 Ermittlung der erforderlichen Bewehrung durch iterative Bestimmung I. Bestimmung des statischen Systems II. Berechnen der Bemessungswerte aus den Einwirkungen und ermitteln des maximalen Momentes MEds. III. 1. Iterationsschritt: Dehnungsverteilung schätzen (s1 und c2) IV. Berechnen von MRds und gleichsetzten mit MEds. Bei starker Abweichung : V. 2. Iterationsschritt: Dehnungsverteilung wird neu geschätzt. VI. Erneutes berechnen von MRds Ist MRds MEds wurde die Dehnungsverteilung gut vorgeschätzt. VII. Ermittel der erforderlichen Bewehrung fyk F mit s 1,15 As 1 sd sd fyd s sd Bemessungstafeln Allgemeines Bemessungsdiagramm Siehe Buch, S. 41 ff. Bemessungstafeln mit dimensionslosen Beiwerten Die Bemessungstafeln sind im Grunde die aufbereitete Form des Diagrammes. Genau wie im Allgemeinen Bemessungsdiagramm dient das bezogene Moment Sds als Eingangswert. Für den einfach bewehrten Querschnitt können die Hilfsgrößen zur Ermittlung des erforderlichen Bewehrungsquerschnittes in der Tabelle abgelesen werden. As 1 1 s1 1 b d fcd N Sd Für den Ansatz einer Druckbewehrung, gelten die gleichen Überlegungen wie im Bemessungsdiagramm. Die Druckzone wird begrenzt auf: x 0,45 Beton bis C 50/60 d x 0,35 Beton ab C 55/67, d Seite 8 Mit dem ermittelten werden in Abhängigkeit von d2/d nun die zugehörigen 1- und 2–Werte abgelesen. Der erforderliche Bewehrungsquerschnitt kann nun berechnet werden: 1 Zugbewehrung As 1 f 1 b d fcd N Sd Druckbewehrung yd As 2 2 b d fcd fyd kd-Tafeln (dimensionsgebundenes Verfahren) =>Schneider S. 5.134 Im kd-Verfahren wird ebenfalls mit Tabellen gearbeitet, die jedoch in diesem Fall dimensionsgebunden sind. Es erfolgt die Ermittlung von k d: kd d cm M Eds [kNm] b[m] 1 Eds f cd Der für die Berechnung des Bewehrungsquerschnitts erforderliche ks-Wert kann nun in der Tabelle abgelesen werden. As1 ks MEds[kNm] d[cm] NEd[kN] Sd Für die Begrenzung der Druckzonenhöhe und einer damit eventuell erforderlichen Druckbewehrung, gelten die gleichen Grenzen wie zuvor: x 0,45 d x 0,35 d Beton bis C 50/60 Beton ab C 55/67, In Abhängigkeit von werden nun die Beiwerte ks1 und ks2 aus einer Tabelle und die Beiwerte 1 und 2 in Abhängigkeit von und d2/d in einer weiteren Tabelle abgelesen. Der erforderliche Querschnitt der Bewehrung ergibt sich aus: As1 1 ks1 MEds[kNm] d[cm] NEd[kN] Sd As2 2 ks2 5.3.2 Querschnitte mit nicht rechteckiger Druckzone MEds[kNm] d[cm] (s.7, Plattenbalken) 5.3.3 Hohlkastenquerschnitt Ermitteln von Sds als Eingangswert in das Bemessungsdiagramm. Sds MSds b d 2 fcd Mit Hilfe von Sds lassen sich alle für die Bemessung notwendigen Hilfswerte in dem Diagramm ablesen. Mit x d wird kontrolliert, ob die Druckzone komplett im Flansch (t i) liegt. Ist x ti kann mit dem ermittelten Sds weitergerchnet werden. Ist x > ti, muss Sds erneut berechnet werden, mit b=bw. ti = „Blechdicke“ im Bereich der Druckzone. bw = Breite des „Balkenstegs“. Hier: bw = 2.t2 t1 Berechnen von t2 1 As 1 1 b d fcd NSd s1 Allgemeines Bei Hohlkästen laufen durch zwei Stege vier Bügelschnitte, die als Querkraftbewehrung anrechenbar sind. Für Torsion sind in einem Steg zwei Bügelschnitte wirksam Seite 9 t2 t3 b Seite 10 5.4 Querkraft (Tragfähigkeit) Berechnung der Schubbewehrung max. Querkraft je Feld verwenden aus den Schnittgrößen (Auflager A-B-C rechts/links je Auflager und beide Seiten des Feldes) 5.4.1 Auflagerart bestimmen direktes Auflager indirektes Auflager (monolithisch) Nachweis wird im Abstand d geführt Nachweis wird am Auflagerrand geführt Fcd,eff Fcd,eff d VSd VSd FA Fsd,eff FA zII Fsd,eff d Auflagernähe von Einzelkräften prüfen: x≤ 2,5*d dann Q oder G mit β abmindern. keine Abminderung von Einzelkräften β = x / 2,5*d VED im Abstand (d + Auflagerlänge) VED im Abstand (Auflagerlänge) gd + qd d + a VED V*ED gd + qd a VED V*ED ACHTUNG: ACHTUNG: bei qd ist auf den Kombinationswert ψ der maßgeblichen Belastung zu achten! (Tabelle siehe Massivbau 1 Seite 4.9) VEd* = VEd-(1,0 d+a) (q+g) bei qd ist auf den Kombinationswert ψ der maßgeblichen Belastung zu achten! (Tabelle siehe Massivbau 1 Seite 4.9) VEd* =VEd – a (q+g) 5.4.2 Prüfen ob Schubbewehrung erforderlich Wird der Nachweis erbracht können die Querkräfte durch das Bauteil (incl. Längsbewehrung) abgetragen werden. Wird der Nachweis nicht erbracht, ist eine Schubbewehrung erforderlich! NW: V * ED VRdct Wird der Nachweis nicht erbracht ist eine Schubbewehrung erforderlich! VRd ,ct 0,1 1 MN 100 l fck 2 m 1 3 0,12 cd MN m 2 bw m d m η1 = Tragfähigkeitsbeiwert η1 = 1,0 für Normalbeton / Leichtbeton siehe Tabelle 11 – DIN 1045-1 1 200 2,0 d mm Beiwert für den Einfluss der Bauteilhöhe Seite 11 l Asl Längsbewehrungsgrad (gewähltes Asl einsetzen) 0,02 A Fläche der Zugbewehrung sl bw d bw Achtung: kleinste Querschnittsbreite innerhalb der Zugzone Für den Hohlkastenquerschnitt darf nur die Längsbewehrung unter den Querkraftübertragenden Teilen (d.h. den Außenstegen) angesetzt werden Dafür wird die effektive Breite der Längsbewehrung ermittelt (t—cnom-???) Asl bw cd 5.4.3 Nachweis der Druckstrebe NSd Ac Fläche der Zugbewehrung (gewählt) kleinste Querschnittsbreite innerhalb der Zugzone NSd Längskraft (Druck (-) / Zug (+) Ac (b * h –AStahlbewehrung vernachlässigen) Wird der Nachweis erbracht kann der Druck durch die Druckbewehrung abgetragen werden. NW: VED VRd max Wird der Nachweis nicht erbracht, muss die Betonklasse erhöht werden. Formel mit 90° (Normalfall) VRd max Vollständige Formel bw z c fcd cot tan VRd max bw z c fcd senkrechte Querkraftbewehrung cot cot 1 cot 2 bw kleinste Querschnittsbreite innerhalb der Zugzone z αc 0,9*d 0,75 * η1 Normalbeton η1=1,0 Leichtbeton Tab. 9.3 DIN 1045-1 Belastungsart reine Biegung Biegung und Längsdruckkraft Biegung und Längszugkraft Druckstrebenwinkel cot θ = 1,2 cot θ = 1,2 θ = 40° θ = 40° cot θ = 1,0 θ = 45° 5.4.4 Ermittlung der Schubbewehrung (Bügel) über den Zugstrebennachweis (Nachweis kommt immer hin, da die ermittelte Bewehrung erst per Mindestbewehrung kontrolliert wird.) Formel mit 90° (Normalfall) lotrechte Schubbewehrung Vollständige Formel asw asw cm2 V ED fysd z cot m cm2 V ED fysd z sin cot cot m asw 2schnittig Wert durch 2 teilen und in Tabelle 4schnittig Wert durch 4 teilen und in Tabelle Seite 12 ACHTUNG: vorgeschätzten Ø des Bügels berücksichtigen! 5.5.5 Prüfen der Mindestbewehrung (s XX oder MBI S.6.21) Egal, ob Schubbewehrung erforderlich oder Bewehrung über Zugstrebennachweis berechnet! 5.5 Torsion (siehe Buch S.54) fyd Bestimmung der Beiwerte fcd und f (siehe Buch S. 42) cd effektive Länge berechnen: leff= ln + a1 + a2 S.4, 3.1 Belastung incl. Kombination berechnen Bestimmung der Momente (Torsionsmoment T und T ed) Bestimmen von MEd Bestimmen von VEd TEd Q T TEd Bild 5.1 5.5.1 Biegebemessung (siehe in dieser FS S. 6 ff.) Durchführen der Biegebemessung für das Bauteil. Hierfür auf die Wahl des Momentes achten!! (Wirkungsrichtung!) Bsp.: Bei einer Belastung wie der in Bild 5.1, ist für die Biegebemessung das Moment aus Q in Feldmitte anzusetzen. T und TEd sind für die Biegebemessung irrelevant. Keine Bewehrung auswählen!! Erf. Biegebewehrung wird am Schluß mit der erf. Torsionsbewehrung addiert und dann ausgewählt!!! 5.5.2 Querkraftbemessung (Annahme: cot = 1,2 oder genaue Berechnung für -> siehe unten) I. Um den Tragsicherheitsnachweis der Torsion durchzuführen muss zunächst das vorhandene Torsionsmoment TE ermittelt werden. II. Falls nicht eine reine Torsionsbeanspruchung vorliegt ist es erforderlich, zunächst den Querkraftnachweis (S.11,5.4) zu führen. VED VRdct sowie VED VRd max III. Prüfen, ob eine zusätzliche Torsionsbewehrung erforderlich ist. ( gilt nur für näherungsweise rechteckige Vollquerschnitte DIN S.83, für alle anderen Querschnitte wird eine Bemessung erforderlich). TEd V ED bw 4,5 4,5 TEd V Rd ,ct V Ed 1 V Ed bw NW: sind die Gleichungen nicht erfüllt wird eine Torsionsbewehrung erforderlich TED TRd,max Druckstrebennachweis (Beton) TED TRd,sy Zugstrebennachweis (Bewehrung) Ermittlung von für nachfolgende Rechnungen erforderliche Werte: für die Ermittlung gibt es zwei Möglichkeiten: 1. Annahme 2. Rechnen = 45°, cot = 1,0 1,2 1,4 cd f cd 0,58 cot VRd ,c 1 VEd ,T V Seite 13 mit: VEd ,T V kN VEd ,T cd NEd i VEd teff bw VEd ,T kN TEd zi 2 Ak [Schubkraft] Bei Druck ist NEd negativ! Ac 1 VRd ,c kN ct 0,1 1 f ck 3 1 1,2 cd f cd t eff m zm 10³ mit cT = 2,4 1 = 1,0 z = 0,9d der kleinere Wert ist maßgebend z=d-2cnom U Uk d t eff 2 c nom d sB sL 2 h d 2 teff zi teff = zweifacher Schwerpunktabstand der Längsbewehrung vom Rand, jedoch nicht größer als die vorhandene Wanddicke = Wandstärke des (Ersatz)Hohlquerschnitts h 0,5 teff 2 teff Ak h 2 2 teff b 2 b(w) zi h 2 d1 d1 h d U k 2 h t eff b t eff 2 h b 2 h b 2 t eff Druckstrebennachweis (max. aufnehmbares Torsionsmoment): TED TRd,max TRd ,max [ MNm] c ,red f cd [ MN / m²] 2 Ak [m²] t eff [m] cot tan c,red = 0,70,751 = 0,5251 (allgemein) c,red = c = 0,751 (Kastenquerschnitt) mit 1=1,0 für Normalbeton Für Leichtbeton s.Tafel 5.32 Zugstrebennachweis: TED TRd,sy Bügel: TRd,sy Asw f 2 Ak cot sw yd Ermitteln der erforderlichen Bügelbewehrung durch Umstellen der Gleichung: a sw TEd ...oder...TRd , sy [kNm] Asw cm² sw m f yd [kN / cm²] 2 Ak [m²] cot Seite 14 Längsbewehrung: TRd,sy AsL Uk fyd 2 Ak tan Ermitteln der erforderlichen Längsbewehrung durch Umstellen der Gleichung: a sl TRd ,sy ...oder...TEd [kNm] Asl cm² Uk m f yd [kN / cm²] 2 Ak m² tan Bei einer kombinierten Beanspruchung durch Querkraft und Torsion Interaktion: -> dazu siehe Bedingungen erläutert unter 5.5.2 TED TRd,max Vollquerschnitt TEd Kastenquerschnitt TRd,max (z.B. Hohlkästen) 2 VEd VRd,max VEd VRd,max 2 1 1 5.5.2 Wahl der Bewehrung (Annahme: normaler Kastenquerschnitt, Druckzone oben, Zugzone unten) Bestimmung der Seitenverhältnisse: (b/h) U 2h 2b xB b U xH h U Längsbewehrung in der Biegezugzone: (meist unten) erf .As AsL x B AsT AsL = erforderliche Bewehrung aus der Biegebemessung AsT = erforderliche Längsbewehrung aus der Torsionsbemessung Längsbewehrung in der Biegedruckzone: (meist oben) AsT = erforderliche Längsbewehrung aus der Torsionsbemessung erf .As x B AsT Längsbewehrung in den Seiten: erf .As x H AsT je Seite!!! AsT = erforderliche Längsbewehrung aus der Torsionsbemessung Bügelbewehrung: erf .asw asw 2aswT asw = erforderliche Bügelbewehrung aus der Querkraftbemessung aswT = erforderliche Bügelbewehrung aus der Torsionsbemessung Seite 15 6. Durchlaufträger 6.1 Bestimmen der ungünstigsten Belastungsfälle 6.1.1 Einfeldträger mit Kragarm qd gd A qd gd max A B VEd max B A B A B qd gd qd gd max MStütz MEd MStütz B A qd gd eld max MFeld A MFeld B 6.1.2 Zweifeldträger qd gd A B qd gd max A C ̂ A B ̂ C qd gd max C VEd max B A B C A B C qd gd max MStütz A B MStütz MEd C qd gd eld max MFeld qd gd A ̂ MFeld B C MFeld 6.2 Momentenausrundung Bei frei drehbar gelagerten Balken und Platten darf das Stützmoment über die Breite der Unterstützung ausgerundet werden M'Ed MEd C Ed CEd,sup a 8 M’Ed MEd Ced = Bemessungswert der Auflagerreaktion = |Qbl|+|Qbr| a = Auflagerbreite a Seite 16 7. Plattenbalken 7.1 Bemessen von Plattenbalken Das Tragverhalten von Balken trifft grundsätzlich auch für Plattenbalken zu. Unterschiedlich ist, dass die in Längsrichtung wirkenden Druckkräfte in die Platte ausstrahlen. Die Platte des Plattenbalkens wirkt als Druckgurt, der Unterzug als Steg und die darin liegende Längsbewehrung als Zuggurt. Für die Bemessung eines Plattenbalkens wird als erstes die Lage der Nulllinie ermittelt. Dies geschieht wie folgt: I. Bestimmung des statischen Systems, einschließlich der effektiven Stützweite. (DIN S.35) II. Berechnen der Bemessungswerte aus den Einwirkungen und ermitteln des maximalen Momentes. => Momentenumlagerung (siehe MB II, S.11.5) sowie –ausrundung (6.2) III. Bestimmung der Baustoffklasse gemäß der Umgebungsklasse IV. Ermittlung der Mindestbetondicke V. Berechnen der statischen Nutzhöhe (ggf. Bewehrung vorschätzen) dsb = 10 mm, dsL = 28 mm (ggf. mehrere Lagen) VI. Ermitteln der effektiven Breite 0 beff bei annähernd gleichmäßig verteilter Beanspruchung (ohne Einzellasten): (vereinfachte Gleichung Annäherung) beff beff ,i bw mit beff ,i 0,2 bi 0,1 l 0 0,2l 0 bi beff genaues Verfahren: (nur wenn gefordert!) Einstegige Plattenbalken und Randträger von mehrstegigen Plattenbalken: beff beff ,1 beff ,2 bw Innenträger von mehrstegigen Plattenbalken: beff beff ,1 beff ,2 bw Verhältnisse ermitteln, von denen die effektive mitwirkende Plattenbreite abhängog ist: hf berechnen und ggf. aufrunden l = Spannweite h h = Höhe des Plattenbalken l bw berechnen bi l berechnen und ggf. aufrunden hf = Dicke der Platte („Flansch“) bw = Stegdicke bi = Plattenbreite Bei Durchlaufträgern und Kragträgern werden anstatt der Spannweite l die Abstände der Momentennullpunkte l0 verwendet. * Durchlaufträger: l0 = 0,8 l für Endfelder l0 = 0,6 l für Innenfelder l0 = 0,4 l für den Stützmomentbereich (mit l=Mittel von l1 und l2) * Kragträger: l 0 = 1,5 lk mit lk = Länge des Kragarms Seite 17 Bezogene mitwirkende Plattenbreite beff,i/bi ablesen und beff,i ermitteln. hf/h l/bw b1/l bzw. b2/l bzw. b3/l 0,7 0,6 0,5 0,4 0,3 1,0 0,9 0,8 0,10 10 20 50 0,18 0,18 0,19 0,20 0,20 0,22 0,22 0,22 0,25 0,26 0,26 0,28 0,31 0,31 0,33 0,38 0,38 0,39 0,48 0,48 0,48 0,15 10 0,19 20 0,20 50 0,23 0,21 0,22 0,26 0,24 0,24 0,28 0,28 0,28 0,32 0,32 0,33 0,37 0,39 0,40 0,44 0,20 10 0,21 20 0,23 50 0,30 0,23 0,26 0,33 0,26 0,30 0,36 0,30 0,34 0,41 0,35 0,38 0,47 0,30 10 0,28 20 0,32 50 0,42 0,31 0,36 0,46 0,35 0,40 0,50 0,39 0,44 0,55 0,44 0,50 0,62 Tab. 7.1 0,2 0,1 0,62 0,62 0,62 0,82 0,82 0,82 1,00 1,00 1,00 0,49 0,50 0,53 0,63 0,64 0,67 0,82 0,83 0,84 1,00 1,00 1,00 0,42 0,45 0,54 0,52 0,55 0,63 0,66 0,68 0,75 0,84 0,85 0,88 1,00 1,00 1,00 0,50 0,56 0,69 0,58 0,63 0,78 0,70 0,74 0,85 0,86 0,87 0,91 1,00 1,00 1,00 beff1/b1 bzw. beff2/b2 bzw, beff3/b3 Bezogene mitwirkende Plattenbreiten beff1/b1 bzw. beff2/b2 bzw. beff3/b3 von Plattenbalken => beff = b * Tabellenwert Im Falle von Einzellasten ist die mitwirkende Plattenbreite im Bereich der Stützmomente mit unten liegender Druckplatte um 40% abzumindern. M 0,6 MEL beff ,red FL beff MFL MEL Grund: Die mitwirkende Breite erfährt unter konzentrierten Einzellasten eine Einschnürung, welche durch Abminderung der Plattenbreite berücksichtigt wird. VII. Berechnen von Sds VIII. In der Tabelle ablesen und nach x auflösen ( = x/d). Daraus ergibt sich nun, ob die Dehnungs-Nulllinie im Steg oder in der Platte liegt. Dehnungs-Nulllinie in der Platte Liegt die Dehnungs-Nullinie in der Platte liegt ein Querschnitt mit rechteckiger Druckzone vor. Es erfolgt eine Bemessung für Rechteckquerschnitte =>a) Biege- & Querkraftbewehrung b) Druck- & Zuggurtbemessung (Kap. 7B) Dehnungs-Nulllinie im Steg Liegt die Dehnungs-Nulllinie im Steg ist die Bemessung mit Tafeln für Plattenbalken erforderlich. Zusätzlich wird die Dehnung in Plattenmitte auf c2 begrenzt. Berechnen von bf 5 gedrungene r Plattenbal ken bw 5 schlanker Plattenbal ken schwach profiliert stark profiliert Gedrungener Plattenbalken (bf/bw<5) Beim gedrungenen Plattenbalken wird der T-förmige Querschnitt in einen äquivalenten Rechteckquerschnitt x d umgewandelt. Hierfür wird wie folgt vorgegangen: I. Ermitteln der Ersatzbreite bi mit Hilfe der Tabelle 1. Hierfür wird hf/d ermittelt, ein aus der Tabelle gewählt und das b in der entsprechenden bfbw-Spalte abgelesen. Seite 18 bf bi=bbf hf h bw II. bi b beff Mit bi wird nun Sds erneut ermittelt und das zugehörige in den Tabellen für rechteckige Querschnitte abgelesen. Ist > gewählt sichere Seite. (Jedoch: je höher die Differenz desto unwirtschaftlicher) Optimal: gew.= berechnet < gewählt unsichere Seite erneute Berechnung mit größerem . III. Mit den so ermittelten Werten kann man in der Bemessungstabelle mit dimensionslosen Beiwerten den mechanischen Bewehrungsgrad ablesen (mit Eds über bi) und die erforderliche Querschnittsfläche der Bewehrung As1 ermitteln. Schlanker Plattenbalken (bf/bw5) Bei schlanken Plattenbalken, oder stark profilierten Querschnitten wird der Anteil der Druckspannungen im Steg in der Regel vernachlässigt. Für die Berechnung gibt es zwei Möglichkeiten: bf hf d c c zs As bw Fc zs=d-0,5 hf Fs I. Berechnung mittels hf/d-Tabellen Ermitteln von hf/d (aus Tabelle) Bilden von beff/bw mit Hilfe von Eds (aus VIII.) aus der Tabelle wählen und die erforderliche Querschnittsfläche der Bewehrung As1 ermitteln. II. Berechnung mittels Spannungsblock: Die Resultierende der Betondruckspannungen wird im Abstand von h f/2 vom oberen Querschnittsrand in der Platte angenommen. hf Somit ergibt sich der innerer Hebelarm wie folgt: z d 2 Die erforderliche Zugbewehrung für einfach bewehrte Plattenbalken berechnet sich mit: 1 MSds As N sd h fyd d f 2 Es wird die Druckspannung c in der Platte nachgeweisen; c MSds fcd hf d bf hf 2 Die Stauchung am unteren Plattenrand c darf 2 0 00 nicht unterschreiten, um eine konstante Spannung in der Betondruckzone zu gewährleisten. hf c c2 s1 hf [cm] c 2 2 0 00 c c 2 d [cm] x s1 2. Variante: Es kann aus dieser Bedingung auch ein Grenzwert für die bezogene Plattendicke hf/d ermittelt werden, welcher bei Verwendung eines S 500 hf/d 0,264 entspricht. Ist die bezogene Plattendicke größer als dieser Grenzwert, ist für die Spannungsverteilung in der Betondruckzone der Völligkeitsbeiwert R zu berücksichtigen. Für die praktische Bemessung empfiehlt es sich bei Überschreiten des Grenzwertes anstelle des Näherungsverfahrens direkt das Bemessungsverfahren mit dimensionslosen Beiwerten anzuwenden. Seite 19 7.B) Anschluss Druck- und Zuggurt Vorgehen für Druck- und Zuggurt Ermitteln der Nulldurchgänge (siehe Seite 17) Ermitteln der Stelle des maximalen Momentes Ermitteln von av (av = halber Abstand zwischen Momentennullpunkt und –maximum) Berechnen der Momente an den Stellen a v und 2*av (max. Moment) => an der Stelle av beträgt das Moment = 0,75*MED,max (wenn nicht umgelagert und ausgerundet werden musste!) Berechnung des maximalen Differenzmomentes: ΔM1=MED,max-MED,av Das größere ist maßgeb.! ΔM2=MED,av-MED,0 Fcd M i z mit z= 0,9· df bf Anschluss Druckgurt beff,1 bw beff,2 VED ermitteln: Ved Fd Fcd Aca Acc Aca=beff,i∙x Acc=(beff,1+beff,2+bw)∙x=bf·∙x Anschluss Zuggurt Wird nur erforderlich, wenn die Zugbewehrung nicht komplett in den Steg gelegt wird. Berechnen der Fläche der gesamten Längsbewehrung ASS [13.2.1 (2)] Berechnen der Fläche der vom Steg ausgelagerten Längsbewehrung Asa VEd ermitteln: Asa = ausgelagerteBewehrung je Seite Ass Asa A Ved Fd Fcd sa Ass Ass =gesamte Bewehrung hf Nachweis für Druck- und Zuggurt: V Ed V Rd ,max VRd ,max c f cd h f av tan cot θ = 40° und cot θ = 1,2 Ermitteln der jeweils erforderlichen Bewehrung: erf .asw VEd tan f yd av Seite 20 => tan θ + cot θ = 2,03333 8. Platten 8.1 Vorbereitung I. Bemessungswert der Einwirkung (gd und qd) bestimmen. Einwirkungen (nur ungünstig, günstig siehe Tab. 2.2,S.3): ständige: gk bestimmen gd = 1,35 gk gd berechnen veränderliche: gegeben oder aus Schneider qk bestimmen qd qk 1,5 qd berechnen Einheit [KN/m2] Einheit [KN/m2] Ψ s. Tab.2.3, S. 4 Summe bilden II. Festlegen des Koordinatensystems - lokales Koordinatensystem je Platte (kürzere Seite = x-Achse, wenn Pieper-Martens wenn nach Hahn, dann ist die x-Achse, die parallel zum freien Rand verlaufende) - globales (allg.) Koordinatensystem V. IV. Bestimmen der effektiven Längen in x- und y-Richtung - l effx l x a x1 a x 2 a1 sowie a2 sind Auflager in x Richtung (1/2 * Auflagerbreite) - l effy l y a y1 a y 2 a1 sowie a2 sind Auflager in y Richtung (1/2 * Auflagerbreite) Bestimmung von Lagerung und Spannungsrichtung der Platte - wenn 2 > - wenn 2 ≤ V. l effy l effx l effy l effx > 0,5 dann Platte als 2-achsig gespannt rechnen ≤ 0,5 dann Platte als 1-achsig gespannt rechnen Ermitteln der Mindestbetondeckung über das Sicherstellen der Dauerhaftigkeit: Annahme: dsl = 10[mm] vorschätzen Umgebungsklasse: XC1 bei Platten (in der Regel) cmin und ∆c aus Tabelle Nachweise: cmin ≥ dsl Bügel sind nicht vorhanden => für punktförmig gestützte Platten: DIN 11.3.2 (3) VI. Ermitteln der erforderlichen Höhe aus Begrenzung der Verformung li m l m 35 d erf i d 35 li m 150 l² d erf i d li m 150 li leff Normale Anforderungen an die Begrenzung der Durchbiegung leff von der größten Platte die kürzeste Seite s. S 62 (Buch) li leff li ist die Ersatzstützweite Höhere Anforderungen an die zur Berücksichtigung des Begrenzung der statischen Systems Durchbiegung umstellen nach d derf ausrechnen herf d erf cnom d sl h= Dicke der Platte herf auf nächst höheren Wert aufrunden Seite 21 herf Mindestdicke einer Vollplatte aus Ortbeton! Mindestdicke: - allgemein 70 mm - Platten mit Querkraftbewehrung: 160 mm - Platten mit Durchstanzbewehrung: 200 mm 8.2 Schnittkräfte bestimmen Auflagerseiten prüfen: Lastabtragung 1- achsig gespannt Lagerung 2-seitig Rechenverfahren als Plattenbalken rechen 2- achsig gespannt 3-seitig Hahn 2- achsig gespannt 4-seitig Czerny oder PieperMartens 8.2.1 einachsig gespannte Platten –zweiseitig gelagertDie Last wird im mittleren Bereich vornehmlich über die kürzere Spannweite abgetragen. NW über Bemessung in Annäherung an aneinanderliegenden Plattenstreifen (ohne Torsionssteifigkeit). Gleichmäßig verteilte Lasten Berechnen der Schnittgrößen über Stabstatik (Balken/Rahmen) an einem 1 m breiten Plattenstreifen. Führen der Nachweise an den maximalen Stellen! max M q l2 8 (Biegung & Längskraft)) max Q q l 2 (Querkraft) In Spannrichtung verlaufende Unterzüge Es treten zusätzliche Biegemomente quer zur Hauptspannrichtung auf. Diese können für verschiedene Lagerungen abgeschätzt werden. (MII, S. 12.8, Bild 12.7) Gefordert wird allerdings nur das Einbringen einer oberen Abreißbewehrung, welche 60% der max. Feldbewehrung entspricht. Öffnungen b lx 5 konstruktive Bewehrung um die Öffnung wird erforderlich b lx 5 Genauer Nachweis erforderlich (Ersatzsystem mit verstärkten Plattenstreifen) (Querzulage zur Rissbreitenbeschränkung, Einfassung der Ränder mit Steckbügeln und bei größerer Beanspruchung die Anordnung von Diagonalstäben in den Ecken) lx b Verstärkte Plattenstreifen in Querrichtung lx Ungestörte einachsige Tragwirkung I. Verstärkte Plattenstreifen In Längsrichtung Einzellasten (MII, S.12.11.) Platte ohne Punktlast berechnen Seite 22 Ungestörte einachsige Tragwirkung II. III. Plattenstreifen infolge der Punktlast ermitteln - Lasteintragungsbreite: t b0 2 d1 d - Mitwirkende Plattenbreite aus Tabelle - Schnittgrößen für Balken (1-achsig gespannt) rechnen Gesamtschnittkräfte m mGleichlast IV. V. M bm v VGleichlast V bm Biegebemessung Durchstanznachweis Momentenausrundung für Zwischenauflager Momentenumlagerungen im Feld (falls ausdrücklich verlangt) 8.2.2 einachsig gespannte Platten –dreiseitig gelagert..... werden nach Hahn gerechnet! 8.2.3 zweiachsig gespannte Platten –vierseitig gelagert- (PIEPER_MARTENS) Bedingungen für die Anwendung: NW: qd 2 gd qd und qd 2 gd 3 Wird eine der Bedingungen nicht erfüllt, kann die Berechnung nicht nach Pieper/Martens erfolgen! Feldmomente und Stützmomente je Platte: (drillsteif rechnen!!! Fall 1) (lokales Koordinatensystem) l effy l effx fy, fx, sy, sx bestimmen mfx, mfy, msx, msy berechnen ist der Verhältniswert der effektiven Stützweiten. ggf. interpolieren Die Stützungsart ist von der Lagerung und dem Koordinatensystem der jeweiligen Platte abhängig. f= Feldmoment s= Stützmoment Siehe Avak II, S. 155, Tab. 6.3 bzw. folgende Seite M Tipp: m-Werte für das globale Koordinatensystem daneben schreiben – einfacher für Mattenberechnung Fd l x2 TW Sind die Einspannmomente von zusammenstoßenden Plattenrändern unterschiedlich, müssen die Momente gemittelt werden. (nicht in sehr steifen Bauteilen) Stützweitenverhältnis: über l1 5 l2 0,5 ms 0,1 ms 0,2 ms 0,75 max ms 0,1 ; ms 0,2 l1 5 l2 ms max ms 0,1 ; ms 0,2 Größerer Wert maßgebend! l1 ist immer die größere Seite der zusammenstoßenden Platten µEds und ω1 Bewehrungsmenge ermitteln und die Mindestbewehrung überprüfen! Querkraftberechnung in den Stützen je Platte: (globales Koordinatensystem) Tafeln Schneider 5. 57 Globales Koordinatensystem maßgebend l __ eff y ist neben der Einspannung maßgebend für die Tafel l __ eff x Seite 23 8.2.4 zweiachsig gespannte Platten –vierseitig gelagert- (Czerny) ständige Lasten: ly max l min l lx Ermitteln des Stützweitenverhältnisses: Ablesen des entsprechenden Tabellenwertes und ermitteln des benötigten Wertes, wie in der Tabelle angegeben. ständige Lasten + veränderliche Lasten: LASTUMORDNUNGSVERFAHREN Bedingungen für die Anwendung: NW: min leff max .leff 0,75 Wird die Bedingungen nicht erfüllt, kann die Berechnung nicht nach dem Belastungsumordnungsverfahren erfolgen! Vorgehensweise: I. Nummerierung der Platten II. Ermitteln des Seitenverhältnisses ly/lx III. Belastungsumordnungsverfahren: Schachbrettartige Aufbringung der Belastung: q ' g q '' p 2 p 2 in allen Plattenfeldern schachbrettartig Ermittlung der maximalen Feldmomente: Symmetrischer Anteil q’ Innenfeld p q ' g 2 Lagerungsbedingungen: Innenränder (Kontinuitätsränder) Außenränder Werte für mxm und my,max ablesen Unsymmetrischer Anteil q’’ p 2 q '' Lagerungsbedingungen: fest eingespannt frei drehbar gelagert allseitig gelenkig gelagert Innenfeld Werte für mxm und my,max ablesen max. Feldmomente: (lx = kurze Seite) q' q'' 2 lx mxm f '( m ) f ' '( m ) xm xm 2 q' q'' l my ,max f '(my ,max ) f ''(my ,max ) x Erhöhung des ermittelten Feldmomentes entsprechend der angenommenen Querdehnzahl: Mxm mxm x x, y s.Tab. 8.2.4 a) & b) My ,max my ,max y auch hier den symmetrischen und den unsymmetrischen Anteil unterscheiden!!! Ermittlung der maximalen Stützmomente: Symmetrischer Anteil q’ q' g Innenfeld p 2 Lagerungsbedingungen: Innenränder (Kontinuitätsränder) Seite 24 fest eingespannt Außenränder p q '' 2 Werte für mx,er min und my,er,min ablesen frei drehbar gelagert Unsymmetrischer Anteil q’’ Rand Lagerungsbedingungen: betrachteter Stützungsrand Übrige Ränder Werte für mx,erm und my,erm ablesen max.Stützmomente: fest eingespannt frei drehbar gelagert (lx = kurze Seite) 2 q' q'' l my ,er min f '(my ,er min ) f ''(my ,er min ) x 2 q' q'' lx mx ,er min f '(m ) f ' '( m ) x ,er min x ,er min Mittelung der Stützmomente über das arithmetische Mittel 8.3 Bemessen im Grenzzustand der Tragfähigkeit fcd 0,85 fck 1,5 fyd fck 1,15 8.3.1 Bemessung der Biegebewehrung Stützung Vorgehensweise: Vorschätzen von mR Beachten: mR Durchmesser der vorgschäten RMatte (z.B. R257A m R=7[mm] dstütze = statische Höhe der Platte über der Stütze Berechnen von dstütze: d stütze hgew cnom mR 2 Berechnung von Eds b=1,0 -Werte, und Aserf bestimmen Auswählen der R-Matte Felder (Platten) Vorgehensweise: Vorschätzen von mQ Formel für Zug oder Druck/ZugBewehrung (Buch s. S. 41 ff) Formel für Zug oder Druck/ZugBewehrung (Buch s. S. 41 ff) Matten siehe Buch Seite 21 evtl. Zulagen wenn R513A nicht ausreicht Flächenbewehrung Buch Seite 19 Beachten: mQ Durchmesser der vorgschäten QMatte (z.B. Q513 A mQ =7,5[mm] _ Berechnen von d x Feld: _ d x Feld hgew cnom Berechnen von d _ mQ 2 mQ d x Feld = statische Höhe der Platte im Feld in globale x Richtung. _ _ y Feld: _ d y Feld hgew cnom Seite 25 d mQ 2 y Feld = statische Höhe der Platte im Feld in globale y Richtung. Erläuterung: Seitenansicht y Draufsicht x dx dy h z dy dx Berechnung von Eds je Feld in globale x und y Richtung. -Werte, und Aserf bestimmen Auswählen der Q-Matte Formel für Zug oder Druck/Zug-Bewehrung (Buch s.S. 41 ff) Formel für Zug oder Druck/Zug-Bewehrung (Buch s. S. 41 ff) Matten siehe Buch Seite 21 evtl. Zulagen wenn R513A nicht ausreicht Flächenbewehrung Buch Seite 19 Nachweis der Mindestbewehrung (Biegebewehrung) Tabelle 4.2 Buch Seite 84 Längs-(Hauptbewehrung) und Querbewehrung 8.3.2 Querkraftnachweis - Prüfen ob Schubbewehrung für Platte erforderlich Wird der Nachweis erbracht können die Querkräfte durch das Bauteil (incl. Längs-bewehrung) abgetragen werden. V *ED VRdct NW: VEd* VEd 1,0 d a q g (direkte Stützung) Wird der Nachweis nicht erbracht ist eine Schubbewehrung erforderlich! Platte 1 VEd1 a Den maximalen VEd-Wert für die Stützung verwenden. (Sollte aus Schneider 5.57 (15.Auflage) je Platte berechnet worden sein) VEd* berechnen: VEd2 Platte 2 VRdct 1 MN 3 MN 0,1 1 100 l fck 2 0,12 cd 2 bw m dm m m η1 = 1,0 für Normalbeton / Leichtbeton siehe Tabelle 11 – DIN 1045-1 1 200 2,0 dStützung mm l Asl= Fläche der Zugbewehrung der Stützung bw= bei Platten = 1,0 [m] NSd= Längskraft (Druck (-) / Zug (+) Ac = (b * h –>AStahlbewehrung vernachlässigen) VRd max bw z c fcd cot tan Mindestbewehrung nach Buch Seite 84 prüfen (b/h) 8.3.3 Nachweis der Druckstrebe Seite 26 Asl 0,02 bw dStützung [MN] Formel mit 90° (Normalfall) Vollständige Formel bw z c fcd cot tan VRd max VRd max bw z c fcd bw= 1,0 [m] bei Platten αc= 0,75 * η1 senkrechte Querkraftbewehrung cot cot 1 cot 2 z = 0,9*dStüzung Normalbeton η1=1,0 & Leichtbeton Tab. 9.3 DIN 1045-1 Belastungsart reine Biegung Biegung und Längsdruckkraft Biegung und Längszugkraft cot θ = 1,2 cot θ = 1,2 Druckstrebenwinkel θ = 40° θ = 40° cot θ = 1,0 θ = 45° 8.3.4 Ermittlung der Schubbewehrung (Bügel) über den Zugstrebennachweis Nachweis kommt immer hin, da die ermittelte Bewehrung erst per Mindestbewehrung kontrolliert wird. 2 Formel mit 90° (Normalfall) asw Vollständige Formel asw as cm V ED fysd z cot m lotrechte Schubbewehrung cm2 V ED fysd z sin cot cot m 2schnittig Wert durch 2 teilen und in Tabelle w 4schnittig Wert durch 4 teilen und in Tabelle Mindestbewehrung nur wenn 5 ≥ b/h ≥ 4 (siehe Buch Seite 84) 8.4 Platten mit Öffnungen l Öffnung wird in der Bemessung nicht berücksichtigt. 5 x b Auslagerung der Bewehrung im Öffnungsbereich. 5 lx b b lx Einteilung der Platte in mehrere Platten um die Öffnung herum b= Öffnungsbreite lx= Hauptabtragungsrichtung „aufgelagerte Platte“: A y x Kx x B B y Flächenlast Seite 27 Die Öffnung gibt die Lage der x-Achsen in den einzelnen Platten vor. (entlang der Öffnung!) Berechnen der effektiven Länge jeder Platte Platte A & Platte B : 3-seitig frei gelagert, Berechnung der Kräfte aus Belastung unter Lastfall 1 = Gleichlast Erhöhung der Momente in x-Richtung um 20 % Lastfall 3 = Randlast ermitteln: zunächst vx und vy (für A mit εA) aus Tabelle ablesen. Diese Werte mit dem unter Lastfall 1 ermittelten K multiplizieren [K x/y=vx/y ∙ K]. Kx und Ky werden dann durch ly von A geteilt und danach mit der Auflagelänge lxvon B multipliziert. Es entsteht so die Randlast S, die auf die Nachbarplatte B wirkt. Mit Hilfe der Hahntafel, die zu der durch Randlast belasteten Platte B gehört die Momente infolge Lastfall 3 (Randlast) ermitteln. Momente aus Randlast und Gleichlast werden addiert 8.4 „Kragplatten“ Balkonob der an Berechnung, Kontrolle, ob Platte 1 als eingespannt betrachtet werden darf NW: MsK 0,5 MsF MsK = Stützmoment aus dem Kragarm 1 Statik (Eigengewicht und ggf Belastung) MsF = Stützmoment aus der Platte q+g wird der Nachweis erbracht, kann der Rand als eingespannt betrachtet werden. Mittelung des Stützmomentes: Die Mittelung der Stützmomente erfolgt nach Schneider. Ist jedoch: Mgemittelt MBalkon wird das Stützmoment des Balkons M e, Balkon q l2 (Gleichlast) angesetzt. 2 Außerdem: Kontrolle, ob d für den vereinfachten NW des Kragträgers maßgebend wird!!! li 35 d li leff Beim Kragträger = 2,4!!! Querkraft für Ve,Balkon= q · l nachweisen 8.5 Allgemein Bei einer Mittelung der Stützmomente bei einem nach Hahn ermittelten Stützmoment mit einem anderen Stützmoment ist es notwendig, das nach Hahn ermittelte Feldmoment zu erhöhen: MFeld (MStütz ,max MStütz ,mittel ) 8.6 Unterbrochene Stützung Ist die linienförmige Unterstützung einer Platte nicht auf einer ganzen Plattenseite unterbrochen wird sie wie folgt berücksichtigt: L = leff = 1,05 * ln mit ln = lichte Weite der fehlenden Unterstützung Seite 28 l/h 7: Konstruktive Bewehrung ohne rechnerischen Nachweis 7 < l/h 15: Bei vorwiegend ruhender Belastung darf auf einen Nachweis nach der Plattentheorie werden, wenn folgende Berechnungsregeln eingehalten werden: verzichtet Schnittgrößen Fd = Fd’ * bf Endauflager: bf = 0,5 ∙ leff tan 60° ≤ 0,5 ∙l1 Zwischenauflager: bf = leff tan 60° ≤ (l1 + l2) ∙ 0,5 Biegebemessung Unterbrochene Stützung am Endauflager beff,F = 0,25 leff beff,S = 0,125 leff Zwischenauflager beff,F = 0,50 leff beff,S = 0,25 leff (mitw. Breite im Feldbereich – Biegebemessung der Feldmomente) (mitw. Breite im Stützbereich – Biegebemessung der Stützmomente) Querkraftbemessung ...ist für einen Rechteckquerschnitt mit einer mitwirkenden Breite beff,V vorzunehmen. Endauflager: beff,V = t + 0,5h Zwischenauflager: beff,V = t + h Querkraftbewehrung, wenn notwendig in form von Bügeln und wie bei Balken bemessen. Bügel müssen die Längsbewehrung unten umschließen, oben genügt es, wenn sie mit Haken verankert sind. Bei deckengleichen Unterzügen an Plattenauflagern wird der freie Rand mit Steckbügeln eingefasst. Bewehrungsführung siehe Avak II, S. 185 Endauflager: Querschnitt der Schenkel der Steckbügel: asw [cm²/m]= 0,1 d [cm] Innstützung: leff ≤ 10h : oben liegende Biegezugbewehrung aus Plattenbemessung ist ausreichend leff > 10h : ∆as° = 0,08 ∙ as° ∙ (leff/h – 10) Zusatzbewehrung ∆as° muss gleichmäßig auf beide Auflagerbereiche des deckengleichen Unterzuges verteilt werden. l/h > 15: Tragverhalten durch genaue Berechnung nach der Plattentheorie. 8.7 Einachsig gelagerte Platten mit Linienlast I. Idealisierte Lastaufstandsbreite ty der Last ermitteln t y b0 2 h1 h II. Mit Hilfe der Tabelle (Avak II, S. 90/91) mitwirkende Lastverteilungsbreite beff bestimmen: muss rechtwinklig zur Stützweite und symmetrisch zum Lastschwerpunkt sein. Seite 29 beff III. IV. Wenn beff > bvorh, dann gilt: red beff beff 2 S Rand Schnittkräfte infolge der Linienlast getrennt für Stütz- und Feldbereiche ermitteln. Dabei stat. System für die Ermittlung von M und V beachten: M kNm m m beff , M V kN v m beff ,V V. „Normales“ Stütz- und Feldmoment aus Gleichlast ermitteln VI. Stütz- und Feldmomente aus Gleich- und Linienlast addieren Seite 30