Kapitel 2: Digitale Signale
Werbung

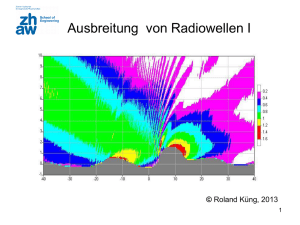
ZHAW, NTM1, HS2008, 2-1 Kapitel 2 Ausbreitung von Radiowellen I Inhaltsverzeichnis 2.1 EINFÜHRUNG IN DIE WELLENAUSBREITUNG........................................................................................... 2 2.2 GRUNDLAGEN ........................................................................................................................................ 3 2.3 BEZIEHUNG ZWISCHEN LEISTUNG UND FELDSTÄRKE ............................................................................. 7 2.4 DIE DREI AUSBREITUNGSMECHANISMEN ................................................................................................ 9 2.4.1 Reflexion .......................................................................................................................................... 10 2.4.2 Beugung........................................................................................................................................... 13 2.4.3 Streuung .......................................................................................................................................... 15 2.5 DAS LINK BUDGET ............................................................................................................................... 15 2.6 LITERATURANGABEN ........................................................................................................................... 19 ANHANG 1: ANTENNE DIAGRAMME UND WERTE .............................................................................................. 20 ANHANG 2: BEISPIEL GSM LINK BUDGET (VEREINFACHT) ............................................................................... 21 © Roland Küng / 2009 ZHAW, NTM1, HS2008, 2-2 2.1 Einführung in die Wellenausbreitung Die Ausbreitung von elektromagnetischen Wellen im Freiraum ist einfach verständlich aber nur für Satrellitenverbindungen nützlich oder allenfalls als Best Case Abschätzung. Die Mechanismen bei der Ausbreitung in Umgebungen sind jedoch vielfältig, können aber den 4 Vorgängen Reflexion, Absorption, Diffraktion (Beugung) und Scattering (Streuung) zugeordnet werden. Cellular Radio Systeme beispielsweise werden meist in städtischer Umgebung (urban) benutzt, wo zwischen Sender und Empfänger meist kein direkte Sichtverbindung (Line of Sight, LOS) besteht. Durch die hohen Gebäude entstehen grosse Beugungsverluste. Durch die mehrfache Reflexion an den Gebäuden und Objekten laufen schliesslich mehrere elektromagnetische Wellen mit unterschiedlicher Weglänge zum Empfänger. Die Interaktion zwischen diesen Wellen am Empfangsort bewirkt Signaladdition oder Signalschwund, je nach Frequenz und Ort, Multipath Fading genannt. Die Stärke der Wellen nimmt ab, wenn die Distanz zwischen Sender und Empfänger zunimmt. Heute existieren viele Kanalmodelle für die verschiedenen praktischen Situationen. Traditionell wird durch diese Modelle die mittlere Feldstärke bei einer bestimmten Distanz vom Sender vorausgesagt, sowie die zu erwartende Abweichung in naher Umgebung des Empfangsortes. Diese, so genannten Large Scale Modelle sind nützlich zur Abklärung der Reichweite, bzw. Abdeckung eines Areals durch einen Funkdienst. Small Scale Modelle geben die schnellen Schwankungen am Empfangsort, wenn man sich um wenige Wellenlängen mit dem Empfänger verschiebt oder kurze Zeit später beobachtet. Small Scale Modelle werden auch Fading Modelle genannt, da sie die zeitliche und örtliche Signalschwankung (Fading) voraussagen. Diese Modelle liefern die Grundlagen für das Design von unterbruchsfreien Empfangssystemen und für die nutzbare Bandbreite eines Kanals. Solches Fading kann bei bewegten Teilnehmern schnelle Signalschwankungen von bis zu 40 dB verursachen, während die Abnahme der mittleren Signalstärke erst mit grossen Distanzverschiebungen spürbar wird. Durch Mittelung vieler instantanen Messungen der Signalstärke über einen Bereich von etwa 5...40 erhält man aus den Werten des Fading Modells die mittlere Feldstärke und deren Abweichung. In Fig. prop.1 ist für einen Indoor Radio Kanal die Empfangsleistung in dBm gegen den Abstand zwischen Sender und Empfänger aufgetragen. Die Mittelung der Werte müssen dem Large Scale Modell dieses Kanals entsprechen, die mikroskopische Fading Struktur hingegen dem Fading Modell. Fig.1. Beispiel Empfangsleistung bei Large Scale und Small Scale Ausbreitung ZHAW, NTM1, HS2008, 2-3 2.2 Grundlagen Die Ausbreitung einer Welle im freien Raum unterscheidet sich ganz wesentlich von derjenigen auf einer Leitung. Wir betrachten, um den Unterschied erkennen zu können, eine Antenne, die eine Welle isotrop mit der Leistung Pt abstrahlt, also in alle Richtungen gleich verteilt. Der Raum in den sich die Welle ausbreitet absorbiere keine Energie, was für Vakuum (Weltraum) immer und die Atmosphäre teilweise zutrifft. Nehmen wir einmal an unser Empfänger könne die Energie auf einer Fläche Ae einsammeln. Am Empfangsort sieht die Welle aus wie ein Ausschnitt aus einer sich in alle Richtungen kugelförmig ausbreitenden Welle, also ein Teil einer Kugeloberfläche. Die Leistung des Senders verteilt auf die Oberfläche von 4r2 beträgt in jedem Abstand Pt. Die Leistungsdichte hingegen wird wegen der mit dem Abstand zunehmenden Kugeloberfläche mit r2 abnehmen. Mit der Fläche Ae verringert sich damit die Empfangsleistung ebenfalls mit r2. Zum Vergleich: ein koaxiales Kabel ohne Verluste würde stets dieselbe Empfangsleistung liefern. Hat die Leitung jedoch Verluste, so würde die Leistung mit konstantem Faktor pro Meter (d.h. um einen konstanten Wert in dB/m) abnehmen unabhängig ob es sich um den ersten oder letzten Meter handelt (Exponentialfunktion (1-a)r ). Die Wellenausbreitung gewinnt also bei sehr grossen Distanzen, dank der Abnahme auf einen Viertel der Leistung (entspricht 6 dB) pro Verdoppelung der Distanz. Dies macht erst eine Funkverbindung zu den entfernten Planeten in unserem Sonnensystem möglich. Als Formel ausgedrückt erhalten wir für die Leistungsdichte p(d) in [W/m2]: p(d) Pt 4d 2 Und für die Empfangsleistung in [W]: Pr p(d) Ae Pt Ae 4d 2 Fig.2. : Modell Freiraumausbreitung Die effektive Antennefläche Ae ist nicht identisch mit der geometrischen Fläche, da nie alle Energie vollständig eingesammelt werden kann. Bei einer Parabolantenne ist der Wirkungsgrad bei etwa 55%, bei einer Hornantenne 75%. Die Berechnung der Dämpfung einer Funkverbindung ist relativ einfach. Man benötigt dazu allerdings einige Begriffe aus der Antennentheorie, welche kurz erklärt sein sollen. Antennen ZHAW, NTM1, HS2008, 2-4 sind die Bindeglieder zwischen den auf Leitungen gebundenen Wellen und jenen im freien Raum. Die einer Antenne zugeführte Leistung wird von dieser immer nur in einen begrenzten Raumwinkel abgestrahlt. Den perfekten Kugelstrahler für elektromagnetische Wellen gibt es nicht, vielmehr konzentriert sich die Leistungsfluss in einen Teil des Raumwinkels, wie dies in Fig. 3 dargestellt ist. Man beschreibt die Abstrahlcharakteristik einer Antenne deshalb mit dem sog. Strahlungsdiagramm, siehe Fig. 3. Fig.3.: Antennengewinn als Resultat der Konzentration der Strahlung in einen Raumwinkel Eine vernünftige Antenne weist eine Hauptkeule auf in deren Richtung die meiste Energie abgestrahlt wird. Man bestimmt den Ort mit der grössten Leistungsdichte (englisch: line of shoot) bei gegebener Distanz. Den gemessenen Dichtewert vergleicht man mit dem theoretischen Wert für einen isotropen Strahler bei derselben Distanz. Das Verhältnis wird als Antennengewinn G bezeichnet. Eine Antenne mit G = 10 dB strahlt somit die zehnfache Leistung in ihrer Hauptstrahlrichtung ab wie der fiktive Rundstrahler bei gleicher zugeführter Leistung. Diese grössere abgestrahlte Leistung in Hauptstrahlrichtung geht verständlicherweise auf Kosten einer kleineren abgestrahlten Leistung in den Grossteil des übrigen Raumwinkels. Die Kontur des Strahlungsdiagramms erhält man, indem man auf dem Kreis in diesem Abstand um die Antenne wandert und die Leistungsdichte bei jedem Winkel bestimmt. Nun werden konzentrische Kreise um die Antenne gezogen, meist log. in dB. Der Kreis durch den Maximalpunkt wird relativ mit dem Wert G in dB geeicht (häufige andere Möglichkeit ist 0 dB als Referenz). Nun lassen sich die zuvor gemessen Werte für jeden Winkel auf dem entsprechenden Kreis markieren. Die Punkte mit halber Leistungsdichte ergeben eine weitere charakteristische Grösse, den Öffnungswinkel der Antenne. Zwischen G und besteht eine approximative Beziehung, falls eine Hauptkeule deutlich dominierend ist: hor vert G 4 bzw . für hor vert 2 G 4 Diese Beziehung kann aber lediglich als Abschätzung dienen. Für die Antenne in Fig. 3 erhält man einen Gewinn von 10 dB und einen Öffnungswinkel von etwa 90o. ZHAW, NTM1, HS2008, 2-5 In Gegenrichtung zur Hauptkeule wird 8 dB weniger Leistung abgestrahlt (ca. 16 %). Ein Empfänger in Richtung 135o würde praktisch gar nichts empfangen, da die Sendeantenne dort eine Nullstelle besitzt. Das Diagramm in Fig. 3 zeigt die relative abgestrahlte Leistungsdichte im sog. Fernfeld der Antenne bezogen auf die Leistungsdichte in der Hauptstrahlrichtung. Man spricht vom Fernfeld, wenn die Wellenausbreitung jene einer rein fortschreitenden Kugelwelle im Raum angenommen hat, was in unmittelbarer Nähe der Antenne nicht der Fall ist. Wo das Fernfeld beginnt, hängt von der Wellenlänge und der Bündelung der Antenne ab. Je stärker die Antenne den Strahl bündelt, umso weiter entfernt von der Antenne beginnt das Fernfeld, ausgedrückt in Anzahl Wellenlängen. Als Beziehung kann für die Grenze Nahfeld – Fernfeld eine der folgenden Ungleichungen geprüft werden: 2D 2 d d d D D ist die maximale physikalische lineare Dimension der Antenne und >> heisst in der Praxis 3…10 Mal grösser. Genau genommen müsste man das Antennendiagramm im dreidimensionalen Raum zeichnen. In der Regel begnügt man sich, dieses in zwei senkrecht aufeinander stehenden Ebenen anzugeben. Diese enthalten immer die Hauptabstrahlrichtung. Man stelle sich dazu die Antenne horizontal ausgerichtet vor. Dann kann man ein Diagramm, wie es Fig.3 zeigt, für die Abhängigkeit vom Azimut angeben, ein zweites gilt dann für die Abhängigkeit von der Elevation. Die beiden Diagramme sind in der Regel nicht identisch (hor ≠ vert) Nun können wir die effektive abgestrahlte Leistung EIRP der Antenne bestimmen, welche die Bündelung der Sendeantenne mit beinhaltet: EIRP Pt G t In der Praxis heisst dies, dass man entweder einen Sender (S) mit hoher Leistung und mehr oder weniger ungebündelter Antenne einsetzen kann oder einen Sender mit geringer Leistung und Bündelantenne mit Gewinn um dieselbe Feldstärke am Empfangsort (E) zu erzeugen (vgl. Fig. 4). Allerdings muss für die Antenne mit Gewinn zumindest die Richtung zum Empfänger bekannt sein. Fig.4: Gleiches EIRP und Empfangsfeldstärke auf verschiedene Art erzeugt ZHAW, NTM1, HS2008, 2-6 Wird dieselbe Antenne als Empfangsantenne benutzt, so hat sie denselben Wert als Gewinn, nun mit Gr bezeichnet. Aus den Beziehungen für die effektive Antennenfläche A und Gr lässt sich folgende Beziehung herleiten sofern Ae >> 2 ist: Gr 4 Ae 2 c f Darin steht für die Wellenlänge und die Lichtgeschwindigkeit c beträgt bekanntlich c = 3*108 m/s. Schliesslich gelangen wir zur meist verwendeten Formel für die Freiraumausbreitung: Pr (d) Pt G t G r 2 (4) 2 d 2 Die Empfangsleistung nimmt also quadratisch mit der Frequenz ab, wenn die Antennegewinne als frequenzunabhängig angenommen werden. Die einzige Möglichkeit dies Auszugleichen sind erhöhte Sendeleistung oder erhöhter Antennengewinn. Letzteres heisst aber auch einen kleiner Raumwinkel zu versorgen und ist nicht in jedem Fall erwünscht. Anders gesagt, für gleiche Ausleuchtung muss die Antenne kleiner gemacht werden, damit ihr Gewinn G konstant bleibt. Dies ist insbesondere bei Satelliten Downlinks zur Erde zu beachten, wo das zu versorgende Gebiet vorgegeben ist und damit der Raumwinkel. Viele Fachleute arbeiten mit der Streckendämpfung PL (englisch path loss), welche üblicherweise als positive dB Zahl angegeben wird. Es gibt zwei interessante Definitionen. Die erste entspricht der Dämpfung, welche man im Labor ohne Antenne und ohne die Strecke zwischen dem Sender S und dem Empfänger E schalten müsste um die gleiche Situation herzustellen: PL SE (dB) 10 log G G 2 Pt 10 log t 2 r 2 Pr (4) d L In dieser Formel taucht noch der Faktor L auf. L steht für irgendwelche Verluste im System (Hardware, Zuleitungen zur Antenne, Filterdämpfung…). Die zweite Definition des Path Loss beschreibt die Dämpfung der Strecke allein, also unabhängig von den Antennen und Losses: PL path (dB) 10 log 4d 2 Im Mobilfunk ist oft die Angabe der Empfangsleistung Pr in dBm (0 dBm = 1 mW an 50 ) üblich: PrdBm (d) 10 log( Pr (d)) 30 Kennt man Pr bei der Distanz do, so berechnet sich Pr im Abstand d von S zu: PrdBm (d) 10 log( Pr (do)) 30 20 log( do ) d ZHAW, NTM1, HS2008, 2-7 In praktischen Systemen für den Mobilfunk, GSM wird Pr (do) häufig im Abstand von do = 100 m und für Indoor PCS, WLAN im Bereich von 1....3 GHz bei do = 1 m gemessen. Die Berechnung der Empfangsleistung an einem Ort d kommt dann ohne Kenntnis der Systemparameter aus. Umgekehrt kann einfach aus dem minimalen Pr, das der Empfänger benötigt (typ. -100 dBm), die Reichweite des Systems ermittelt werden. Das Freiraummodell liefert in diesen Anwendungen aber viel zu optimistische Resultate, de facto den Best Case. Beispiel GSM Zelle mit Basisstationsantenne mit D = 1 m operiert bei 900 MHz. Der Sender arbeitet mit 10 W und Gt = 5. Das Handy hat Gr = 1 und arbeitet ab -90 dBm Empfangspegel korrekt. Die Distanz d muss grösser als 6 m sein, damit die Formeln bei Sichtverbindung gelten. EIRP = 50 W oder entsprechend 47 dBm Die Empfangsleistung in 100 m Distanz in Richtung max. Antennen gain beträgt: Pr (100) 10(5)(1)(1 / 3) 2 3.5W 24.5dBm (4) 2 (100) 2 (1) In 10 km Abstand ergibt sich: PrdBm (10000) 10 log( Pr (100)) 30 20 log 100 64.5dBm 10000 Die Zellengrenze wäre max. bei 200 km, allerdings ist dies nur ein theoretischer Wert in hügeligem und überbautem Gelände. 2.3 Beziehung zwischen Leistung und Feldstärke Die Beziehungen der Freiraumausbreitung sind auch als Funktion der elektrischen Feldstärke E am Empfangsort von grossem Interesse. Insbesondere im Bereich elektromagnetische Verträglichkeit (EMV, EMC) werden die zulässigen Limiten in V/m im Abstand d spezifiziert. Im Weiteren werden nicht angepasste elektrische Empfangsantennen oft hochohmig abgegriffen, so dass die Berechnung der Empfangsspannung über die Feldstärke eine einfache Abschätzung erlaubt. Ohne die Maxwell’schen Gleichungen zu bemühen sei festgehalten, dass jede strahlende Struktur eine strahlende Feldkomponente proportional zu d-1 besitzt, eine induzierende Komponente proportional d-2 und eine statische Komponente proportional d-3. In der Fernfeld Region dominiert klar die strahlende Komponente, so dass man die anderen nicht berücksichtigen muss. Die Folgen von Maxwells Gleichungen sind in Fig. 5 graphisch dargestellt. Im Freiraum ist ferner bekannt, dass sich E und H Komponente zueinander verhalten wie: E R fs 120 377 H Das Verhältnis E zu H heisst Freiraum Impedanz Rfs. ZHAW, NTM1, HS2008, 2-8 Fig. 5: Maxwell und die elektromagnetische Strahlung Berechnet man aus der abgestrahlten Leistung EIRP die Leistungsdichte p(d) am Ort d so ergibt sich: 2 E PG EIRP p(d ) t t2 E H 2 R fs 4 d 4 d bzw. E (d ) 30 EIRP d Die Einheit von p(d) ist W/m2. In bekannter Weise hängt die empfangene Leistung Pr(d) von p(d) ab: 2 2 G r 2 Pt G t G r 2 Pr (d) p(d) A e Ae 120 120 4 (4) 2 d 2 E E Im Beispiel des letzten Kapitels berechnet sich die Feldstärke in d = 10 km Distanz zu 3.9 mV/m. Oft interessiert die Eingangsspannung am Empfänger, welche vom Hersteller meist mit Empfindlichkeit bezeichnet wird. Typische Werte sind 0.3...3 V. Hier muss nun unterschieden werden, ob eine an den ersten Verstärker angepasste Antenne (meist 50 Ohm) verwendet wird oder eine Drahtantenne, die auf einen hochohmigen Eingang führt. Bei den Frequenzen um 1 GHz und höher ist die angepasste Antenne optimal, ihre Länge von /2 oder /4 ist akzeptabel und die niederohmige Impedanz verhindert parasitäre Filterdämpfungen. Bei diesen Antennen ist entweder Ae oder Gr bekannt. Die Empfangsspannung in diesem Fall beträgt: V Pr (d ) R ant E 2 G r R ant 120 4 Rant ist in dieser Beziehung der Antennenwiderstand und als Folge der Anpassung auch der Eingangswiderstand des Empfängers. Pr(d) entspricht ja definitionsgemäss der Leistung am Empfängereingang bei Anpassung. Bei tiefen Frequenzen wird eine elektrische Antenne oft sehr viel kürzer bemessen als und die Empfangsspannung hochohmig abgegriffen. Man möchte also die Leerlaufspannung der kurzen Antenne benutzen. Die beiden Modelle sind in Fig. 6 vereinfacht skizziert. Eine ZHAW, NTM1, HS2008, 2-9 genaue Rechnung ist hier schwierig, da die Antenne zudem kapazitiv wirkt (C in Serie zu Quellenwiderstand). Als obere Grenze kann für eine Länge l gerechnet werden mit: V l E Anstelle von l ist genauer die effektive Länge bzw. Höhe der Antenne einzusetzen (siehe Tabelle Antennen in Beilage). Für das betrachtete Beispiel ergibt sich bei angepasster Antenne und Rant = 50 eine Spannung von V = 0.13 mV. Die Wellenlänge beträgt übrigens 33 cm. Bei einer Drahtantenne von 3 cm ergäbe sich bestenfalls V = 0.12 mV. Fig.6: Modelle zur Bestimmung der Empfängerspannung 2.4 Die drei Ausbreitungsmechanismen Reflexion, Beugung und Streuung sind die drei grundlegenden Ausbreitungsmechanismen, welche die reine Freifeldausbreitung beeinflussen, wenn anstelle der Satelliten Links Verbindungen im Bereich von Siedlungen und innerhalb von Häusern betrachtet werden. Dies trifft in starkem Mass bei den Mobilfunksystemen(GSM, 3G...) und den Personal Communication Systemen (DECT, WLAN) zu. Da die Vorgänge mathematisch sehr komplex zu berechnen sind, lassen sich nur sehr einfache Geometrien ohne grossen Computeraufwand (wie etwa Ray Tracing) behandeln. Dieses Kapitel beschränkt sich auf die allerwesentlichsten, dafür praktisch nutzbare Zusammenhänge mit dem Ziel das Phänomen und die Konsequenz zu verstehen. Fig. 7: Die Ausbreitungsmechanismen ZHAW, NTM1, HS2008, 2-10 2.4.1 Reflexion Reflexion (englisch Reflection) tritt auf, wenn eine elektromagnetische Welle auf ein Objekt trifft, welches ebene Ausdehnungen > aufweist. Beispiele sind Erdboden, Häuserfronten, Zimmerwände. Genau genommen teilt sich die einfallende Welle auf in einen reflektierten Anteil und einen ins Material eindringenden Anteil (Absorption). Ideal leitende Flächen reflektieren die Welle vollständig, ideale dielektrische Materialien (Keramik, Glas, reines Wasser, RF-Printmaterial...) reflektieren einen Teil und lassen einen Teil durch ohne Verluste zu erzeugen. Reale Materialien reflektieren einen Teil und lassen einen Teil durch, der sich durch Verluste in der Folge beim Durchlaufen des Materials (Absorption) abschwächt. Uns interessiert an dieser Stelle nur der reflektierte Anteil. Der Grad der Reflexion wird durch den komplexen Reflexionskoeffizienten beschrieben. Dabei wird der E- Feldstärkevektor zerlegt in eine zur Reflexionsfläche senkrechte und eine parallele Komponente. Nahezu ideale Leitermaterialien nutzt man in der Praxis als Abschirmung von elektromagnetischen Wellen aus. Die ganze Energie wird reflektiert. Sind solche grossen Flächen im Ausbreitungsbereich vorhanden so entsteht neben dem direkten Freifeldpfad (Sichtverbindung zwischen S und E) ein zweiter Ausbreitungspfad. Als nächst besseres Modell der Ausbreitungstheorie wird für den Mobilfunk deshalb das sog. 2-Ray Model benutzt. Es berücksichtigt den direkten Pfad (englisch Line of Sight - LOS) und den am Boden (Wand) reflektierten Pfad. Fig. 8 zeigt eine Situation mit einer Reflexion am Boden. Der Sender befindet sich in Höhe ht und der Empfänger in Höhe hr. Fig. 8: das 2-Ray Reflexions-Modell In vielen Mobilfunk Anwendungen beträgt die Distanz zwischen Sender und Empfänger max. einige 10 km. Der Boden kann mit Ausnahme der Alpenländer meist als flach betrachtet werden. Übrigens sind in der Schweiz für die Einführung von Natel C und GSM intensive eigene Forschungsarbeiten der Telecom nötig gewesen, um die Reflexionen an den Bergwänden mit in die Modelle einbeziehen zu können. Die E-Feldstärke sei vertikal polarisiert, d.h. die Stabantennen zeigen, wie uns gewohnt senkrecht zur Erde. Die totale empfangene Feldstärke Etot ist die Summe der direkt einfallenden Komponente ELOS und der am Boden (ground) reflektierten Komponente Eg. Kennt man die Freifeld-Feldstärke Eo in der Referenzdistanz do, so gilt für d > do für die Freiraumwelle: E(d, t ) Eo do d cos(c ( t )) d c Die zwei Komponenten ELOS und Eg berechnen sich somit nach Fig. 7 zu: ZHAW, NTM1, HS2008, 2-11 E LOS (d' , t ) Eo do d' cos(c ( t )) d' c E g (d' ' , t ) Eo do d' ' cos(c ( t )) d' ' c Zwar geschieht die Reflexion genau genommen entsprechend den physikalischen Gesetzen, aber für kleine Winkel findet man, dass die reflektierte Welle Eg praktisch gleich in der Amplitude ist wie die einfallende Welle Ei , hingegen um 180o in der Phase gedreht, d.h. = -1. Dies gilt auch wenn der Boden nicht perfekt leitend ist für Einfallswinkel von einigen Grad recht gut und sowohl für vertikale wie horizontale Polarisation. Das vereinfacht die grobe Rechnung massiv, es lässt sich der Betrag des Etot Vektors bestimmen als Betrag der Summe der beiden Teilkomponenten. Drückt man im weiteren d’ und d’’ durch die horizontale Distanz d und die Antennenhöhen über Boden ht und hr aus und nimmt an, dass d >> ht + hr ist, so lässt sich der Laufzeitunterschied der beiden Wellen berechnen zu: d 2 ht hr cd ELOS und Eg sind in ihrem Betrag näherungsweise gleich gross. Diverse Winkel- und Trigonometrie Umformungen liefern schlussendlich das interessante Resultat: E tot (d) 2 Eo do sin d c 2E d sin d c d 2 2 c ist die Trägerfrequenz der Funkwelle, c die Lichtgeschwindigkeit, Ed die Freiraum Feldstärke im Abstand d. Die Formel gilt etwa ab einer Distanz von d = ht + hr und zeigt dass frequenzabhängig und geometriebedingt Auslöschungen auftreten können. Diese Auslöschungen kennt jeder als Funklöcher, ein wenig sich drehen oder weggehen behebt die Situation beim Handy meist. Durch die Überlagerung mehrerer Reflexionen und Reflexionskoeffizienten < 1 wird der Pegel in diesen Funklöchern aber in der Praxis nie ganz zu Null. In fixen Mikrowellenverbindungen (z.B. zwischen den Dächern zweier Häuser) lässt sich die Geometrie im Gelände so planen, dass der Reflexionspunkt nicht existiert oder stört und daher dort die Freiraumformel recht gut gilt. Mit der Beziehung zwischen Pr(d) und E(d) gilt für die Empfangsleistung: 2 h T h R Ae 2 2 h T h R sin 4Pt G t G r sin 4 d d 120 d 2 Pr 4 E d 2 2 Fig. 9 zeigt den theoretischen Verlauf der Empfangsleistung in Funktion der Distanz. Die Formel für das 2-Ray-Model wird häufig weiter vereinfacht, indem man die Approximation sin(x) x benutzt. Dies gilt gut sofern x < 0.628 rad ist. Das wiederum entspricht einer minimalen Distanz: d 10h t h r Die Feldstärke wird in diesem Fall: E tot (d) 2E 0 d 0 2h t h r d d h 2t h 2r Pr Pt G t G r 4 d ZHAW, NTM1, HS2008, 2-12 Bei grossen Distanzen geht die Empfangsleistung also mit d4 zurück, also 40 dB pro Dekade. Dies ist in dB doppelt soviel wie bei der Freiraum- Ausbreitung. Weiter interessant ist, dass bei grossen Distanzen die empfangene Leistung und die Streckendämpfung frequenzunabhängig werden, was allerdings in der Praxis schon nicht ganz stimmt. Fig. 9: Variation der Empfangsleistung mit der Distanz bei idealer Reflexion Beispiel: Mobiles Fahrzeug im Abstand von 5 km von der Basisstation. Autoantenne ist eine vertikale /4 Monopol Antenne mit Gr = 2.55 dB Eine Messung des Netzbetreibers liefert in do = 1 km Abstand eine Feldstärke von Eo = 10-3 V/m. Die Trägerfrequenz beträgt 900 MHz. Die Senderantenne ist auf einem 50 m hohen Turm aufgebaut, die mobile Antenne auf 1.5 m Höhe platziert. Welche Feldstärke und Leistung findet man in 5 km Distanz zur Basisstation vor? Die Wellenlänge ist somit c/f = 0.333 m. Die Antennenlänge beträgt also beim mobilen Teilnehmer l = 8.33 cm Das lineare Gain Gr beträgt 1.8 Die Gleichungen gelten für Distanzen d > 2250 m E tot 2 10 3 10 3 2 50 1.5 113 10 6 V / m 5 10 3 0.333 5 10 3 Pr (5000) = 0.54 pW bzw. -92.7 dBm ZHAW, NTM1, HS2008, 2-13 2.4.2 Beugung Die Beugung (englisch Diffraction) erlaubt den Funksignalen auch hinter Hindernisse zu gelangen, zu Orten, welche keine direkte Sichtverbindung (NLOS) haben. Obwohl die Feldstärke sehr rasch abnimmt, wenn der Empfänger tiefer in die abgeschattete Region (shadow) eindringt, ist in vielen Fällen ein Empfang noch möglich und ermöglicht erst eine flächendeckende Erschliessung eines Gebietes. Da oft in diesem Fall die Reflexion wegfällt (durch Hindernis ausgeschaltet) bildet der Ausbreitungsverlust für Freiraum die Referenz für die Berechnung des Empfangspegels. Die Beugungstheorie liefert zum Freiraum-Wert einen zusätzlichen Beugungsverlust. Fig. 10 zeigt schematisch die Situation, wenn ein mobiler Teilnehmer sich hinter einem Hindernis mit markanter Kante (Haus, Hügelkuppe) bewegt. Fig. 10: Empfang bei abgeschatteter Situation Die Theorie zur Berechnung der Dämpfung ist sehr kompliziert und von Fresnel und Kirchhoff entwickelt worden. In vereinfachenden Modellen ist der so genannte Knife-edge Beugungspunkt K massgebend, der die kürzeste Verbindung Sender - Kante - Empfänger markiert. K liegt im Abstand r1 von der Sendeantenne und r2 von der Empfangsantenne. Die virtuelle Sichtverbindung liegt bei K um die Höhe hp unter dem Punkt K. Nun kann auch im echten LOS Fall eine Beugung an einer Kante auftreten, so dass hp positiv oder negativ sein kann. Für die Voraussage des Beugungsverlustes wird nun ein Diffraktions-Faktor v berechnet: v h p 2 1 1 ( ) r1 r2 Mit diesem Parameter v kann man in einer Graphik den Verlust im Vergleich zum nicht sichtbehinderten Fall (LOS) herauslesen. Diese Graphik ist in Fig. 11 wiedergegeben. Die Kurve zeigt, dass bei Streifen eines Hindernisses (hp = 0) eine Zusatzdämpfung von 6 dB eintritt (im Vergleich zu Freiraum). Bei v >> 0 nimmt die Wahrscheinlichkeit einer Reflexion zu, so dass dann die zugehörigen Formeln gelten. Bei v << 0 befindet man sich deutlich im Funkschatten und der Verlust nimmt mit 20 dB pro Dekade in v zu. Je höher die Frequenz, desto mehr nimmt der Betrag von v zu und damit die Dämpfung auch. ZHAW, NTM1, HS2008, 2-14 Fig. 11: Beugungsverlust im Funkschatten Beispiel: r1 = 5.28 km r2 = 2.88 km hp = 19.5m Frequenz f = 850 MHz Der Parameter v berechnet sich zu: v 19.5 2 1 1 ( ) 1.08 35.1 5.28 2.88 In der Graphik Fig. 11 liest man zu diesem Wert eine Dämpfung von 14 dB heraus. Diese Dämpfung addiert sich zu der Freiraumdämpfung für die Distanz d = r1 + r2. In der Praxis, speziell in hügeligem Gelände, stehen meist mehrere Hindernisse im Weg. Die totale Beugung muss in diesem Fall mit speziellen Computerprogrammen berechnet werden. ZHAW, NTM1, HS2008, 2-15 2.4.3 Streuung Ebene Flächen, welche deutlich grösser sind als eine Wellenlänge können als Reflektoren behandelt werden. Oft sind aber die Oberflächen weniger flach und rau beschaffen. Gerade in städtischer Umgebung stehen viele Objekte, welche Funkwellen nicht einfach reflektieren, sondern in alle Richtungen streuen (englisch: Scattering). Es gibt einige Theorien, wie Streuung in den Ausbreitungsverlust einzubeziehen ist. Einige benutzen modifizierte Reflexionsfaktoren andere die sog. Radar Cross Section Faktoren (RCS), die für verschiedene Gebäude und Städtetypen experimentell bestimmt wurden. Eine noch einfache, empirische Formel (Rappaport, [3]) für die rückgestreute Leistung in Richtung des Empfängers lautet: PR (dBm) PT [dBm] G T [dBi ] 20 log( ) RCS[dB m 2 ] 30 log( 4) 20 log( d T ) 20 log( d R ) Hierin bedeuten PR die rückgestreute Leistung in Richtung E und dT und dR die Distanzen vom Streuer zu S bzw. E. Für mittlere Gebäude wurde ein SCR von 14 dB m2 ermittelt und für grosse Gebäude 56 dB m2, wenn diese jeweils etwa 5-10 km von S und E entfernt sind. In einigen Fällen helfen diese rückgestreuten Leistungen für eine Verbindung, in anderen zerstören sie die über andere Wege eintreffende Feldstärke bei ihrer vektoriellen Addition und erzeugen eine variierende Feldstärke Landschaft wie in Fig. 12 dargestellt. Fig.12: Streuung und Beispiel einer resultierenden Feldstärkeverteilung 2.5 Das Link Budget Ist die Ausbreitungsdämpfung einmal erst bekannt, durch Simulation und Messung mit den notwendigen Korrekturen versehen, so kann für ein Kommunikationssystem ein so genanntes Link Budget erstellt werden. Dabei sind spätestens hier die festgesetzten gesetzlichen Bedingungen der Zulassungsbehörden mit einzubeziehen. Meist sind abgestrahlte Leistung EIRP und Bandbreite des Kanals vorgegeben. Die Physik der Rauschprozesse stellt beim Empfänger die andere Grenze dar. Neben allfälligen Rauschbeiträgen im Übertragungskanal oder gar Interferenzen mit schmalbandigen Signalen bildet letztlich das Eigenrauschen des Empfängers eine Grenze für die noch nutzbare Empfangsleistung. Gehen wir im Folgenden davon aus, dass dieses Empfängerrauschen limitierend wirkt. Im Weiteren sei vorausgesetzt, dass in der Verarbeitungskette innerhalb des Empfängers der Signalpegel immer deutlich über dem Pegel am Empfängereingang liegt. Dies bedeutet in der Praxis dreierlei: ZHAW, NTM1, HS2008, 2-16 1. 2. 3. Am Eingang des Empfängers befindet sich ein rauscharmer Verstärker mit einem Gain von typisch 20 dB. Verluste in nachfolgenden Stufen wie Mischer (7 dB), Filter (4 dB), Attenuatoren für Matching ( X-dB), Power Splitter (3 dB, 6 dB) sind sofort durch Verstärker wieder auszugleichen, so dass der Signalpegel nie deutlich (mehr als 10 dB) unter den Ausgangspegel des ersten Verstärkers fällt. Die Rauschzahlen der Nachfolgeblöcke sind so gewählt, dass deren auf den Empfängereingang bezogenen Geräuschleistungsdichten diejenige des ersten Verstärkers deutlich unterschreiten. Diese beiden Massnahmen erleichtern die Betrachtung, weil nun sichergestellt werden kann, dass die Rauschbeiträge der dem ersten Verstärker nachfolgenden Blöcke kaum einen Einfluss haben auf die Grenze des Empfangsbereich. Stillschweigend wird jedoch dabei vorausgesetzt, dass die Rauschzahlen, bzw. Rausch-Ersatzquellen der Nachfolgeblöcke so ausgewählt werden, dass deren inhärente Geräuschleistungsdichte diejenige der Ersatzquelle der Vorstufen deutlich übertrifft. In der Praxis bedeutet dies, dass das empfangene Signal sobald es die Dynamik erlaubt kontinuierlich weiter verstärkt werden soll und grundsätzlich bis zur Basisbandstufe nur rauscharme Komponenten in Frage kommen. Besonders übersichtlich ist dies bei einer Verstärkerkette mit den Stufen 1, 2 und 3 mit entsprechend indexierten Verstärkungen (Gain) G und Rauschzahlen F. Die gesamte Rauschzahl der Kette beträgt in linearer Darstellung: Ftot F1 F F2 3 F1 G 1 G 1G 2 Sie wird ungefähr gleich F1 wenn die Verstärkungen nicht sehr klein sind und die Rauschzahlen nicht sehr gross sind. Besonders der erste Verstärker sollte also selber extrem rauscharm sein (F < 2). Man verwendet dazu so genannte Low Noise Amplifier (LNA). Die Rauschzahl wird häufig bereits in dB angegeben und dann oft mit NF (englisch Noise Figure) bezeichnet. NF 10 log( F) Man sollte sich immer genau klar sein ob man linear oder in dB abliest und rechnet! Die Rauschzahl Ftot und Bandbreite B des Empfängers bestimmen bei gutem Design die Rauschleistung N bezogen auf den Eingang. Als Bandbreite gilt in der Regel die schmalste Filterbandbreite im System und diese befindet sich meist bei einer Zwischenfrequenz oder im Basisbandteil des Demodulators. N Ftot k T B In dB ausgedrückt: NdBm 10 log( kT) 10 log( B) 10 log( Ftot ) 174dBm / Hz 10 log( B) NFtot Der kT Term entspricht für Anwendungen im Raumtemperaturbereich einem Wert von 174 dBm/Hz. Unter diesen Wert kann man ohne extreme Kühlung nicht kommen. Ist z.B. in einem Empfänger die Bandbreite auf 10 kHz begrenzt und die Rauschzahl des ersten LNA betrage 4, so beträgt die relevante Rauschleistung am Eingang N = -174 dBm + 40 dB + 6 dB = -128 dBm. Das Nutzsignal sollte diesen Wert also nicht unterschreiten. Im Gegenteil, für eine brauchbare Empfangsqualität ist sogar ein gewisses Signal/Geräuschverhältnis S/N notwendig. Die Grenze für eine brauchbare Empfangsleistung ist also noch weiter oben anzusetzen. Für analoge Übertragungen um grob 20...40 dB, für FSK ZHAW, NTM1, HS2008, 2-17 um ca. 10 dB und für PSK um ca. 6 dB. Die Zahlen sind jedoch sehr stark abhängig von den gewählten Implementationen im Demodulator und den erlaubten Fehlerraten, welche noch von der Signalverarbeitung korrigierbar sind. Wer lieber in Volt statt dBm rechnet, erinnere sich daran, dass 0 dBm genau 1 mW an 50 entspricht. 1 Vrms entsprechen also -107 dBm und 0 dBm sind 224 mVrms. In der Folge wird aber ausschliesslich mit den in der HF üblichen dB und dBm Werten gerechnet! Der empfangene Pegel am Eingang des Receivers ist gegeben durch die abgestrahlte Leistung EIRP zuzüglich dem Antennengewinn des Empfängers, abzüglich der Streckendämpfung PLpath und Implementationsverluste L: Pr (dB) EIRP G r L PL path Die Streckendämpfung wird dabei unabhängig von den Antennengewinnen als wirklichen „Luft-Streckenverlust“ linear definiert zu: PL path Pt G t G r Pr L PLpath in dB ist für den Freiraum wie weiter oben bereits berechnet: PL path 10 log 4 d 2 Mit EIRP in dBm ist auch Pr in dBm, d und sind in gleichen Einheiten einzusetzen. Pr entspricht der Signalleistung S am Empfängereingang und muss nun für eine taugliche Verbindung grösser sein als die Summe von N und dem notwendigen S/N für den Demodulator. Die Gleichung für ein Link Budget (alle Terme in dB) lautet also: EIRP dBm G r L PL path 174dBm / Hz NFtot 10 log( B) min( S / N) Der Sachverhalt lässt sich auch graphisch gut in einer Säule darstellen (Fig. 12) Fig. 12: Link Budget: Terme und Berechnung ZHAW, NTM1, HS2008, 2-18 Beispiel: Ein 433 MHz Telemetrie Link soll möglichst weit Daten übertragen können. Das ETSI (europ. Behörde) schreibt 10 dBm EIRP und 25 kHz Bandbreite für eine konzessionsfreie Verbindung vor. Die geometrisch klein gehaltenen Antennen haben einen Gewinn von 3 dB. Der LNA im Empfänger hat ein NF von 14 dB. Die Ausbreitung sei nach Freiraum. Antennenkabel und Filter vor dem LNA haben zusammen L = 2 dB Verlust. Der Demodulator arbeitet noch bei einem S/N von 12 dB genügend. Die Wellenlänge beträgt = 70 cm N am Empfängereingang beträgt: N 174dBm 14dB 10 log 25kHz 116dBm Die minimale Pr beträgt somit: -116 dBm + 12 dB = -104 dBm Der maximal mögliche Path Loss ergibt sich daraus zu: PL path EIRP G r L Pr 115dB Setzt man dies in die Formel PLpath ein: PL path 10 log 2 (4) 2 d 2 und löst nach d auf, so erhält man eine Distanz von 31 km. Dies ist aber ein theoretischer Wert. Wir werden im nächsten Kapitel sehen, dass in der Formel fur Pr anstelle des Terms d2 eher dn tritt mit n im Bereich 2…6. Unberücksichtigt sind all die durch Mensch und Maschinen verursachten Stör- und Rauschanteile (z.B. 3. Harmonische eines 140 MHz Prozessors, 430 MHz Amateursignale...) In Wirklichkeit werden die Link Budgets detailliert, z.B. als Excel-Sheet, erfasst und von der Senderausgangsstufe bis zum Demodulator erfasst. Hierzu ist dann aber Kenntnis des ganzen geplanten Systems notwendig. So muss man bereits wissen, welche Modulationsart verwendet wird, welchen Kodierungsgewinn man erreichen kann, ob Spread Spectrum Technik angewandt wurde und welche Fehlerrate (Eb/No) man einhalten muss. Dazu muss die Implementation so klar sein, dass die Verluste aller Massnahmen ebenfalls bekannt sind und verrechnet werden können. Ein Wort noch zur Genauigkeit. Ob man 1 dB mehr oder weniger empfängt spielt in mobilen Funkstrecken am Boden keine so grosse Rolle, da zeitliche Schwankungen von mehreren dB auftreten. Bei Punkt-Punkt Richtverbindungen bedeutet 1 dB hingegen schon einiges und bei Satellitenverbindungen ist es ein markanter Unterschied. ZHAW, NTM1, HS2008, 2-19 2.6 Literaturangaben [1] Wireless Communications, Theodore S. Rappaport, ISBN10- 0-7803-1167-1, IEEE 1996 [2] Communication Systems Engineering, John Proakis, Masoud Salehi, ISBN-10: 0130617938, Prentice Hall 2001, auch in deutsch erhältlich: ISBN-10: 3827370647 [3] Kommunikationstechnik, Martin Meyer, ISBN-10: 3834804657, Vieweg+Teubner, 2008 [4] Antennas and Propagation, Simon Saunders, ISBN10- 0-471-98609-7, John Wiley, 1999 [5] Quantifying Short-Range Surface to Surface Communications Links, W.M. Merrill et.al., IEEE Antennas and Propagation Magazine, Vol.46 No.3 June 2004 [6] Einfacher Funkkanal-Simulator: http://www.cjseymour.plus.com/software.htm, 2004 V1.10 oder http://www.rfglobalnet.com/download.mvc/RFPROP-Version-103-0001 V1.03 [7] Okumura-Hata Modell: Java Tool: http://www.cdt21.com/resources/siryo4_01.asp 2-Ray Model: Java Tool: http://www.cdt21.com/resources/siryo5.asp ZHAW, NTM1, HS2008, 2-20 Anhang 1: Antenne Diagramme und Werte ZHAW, NTM1, HS2008, 2-21 Anhang 2: Beispiel GSM Link Budget (vereinfacht)