PS Arbeit zum Thema COMPUTERTOMOGRAPHIE

25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
PS Arbeit zum Thema COMPUTERTOMOGRAPHIE
Die Computertomographie (abgeleitet aus dem Griechischen: „tome“= Schnitt,
„graphein“=einritzen,zeichnen, schreiben) ist ein Hilfsmittel in der Medizin, das
beinahe ebenso bekannt ist wie das klassische Röngten. Wie bei vielen anderen
technischen und naturwissenschaftlichen Erfindungen spielt jedoch auch hier die
Mathematik eine wesentliche Rolle, die ein Entstehen bzw. Funktionieren dieser
Untersuchungsmethode erst ermöglicht. Ziel dieser Arbeit soll es nun sein, einerseits
das nötige Hintergrundwissen über Nutzen und Einsatzmöglichkeiten in der Medizin
sowie über die Physik , die die Funktionsweise erklärt, zu vermitteln und andererseits
natürlich die Bedeutung und das konkrete Vorkommen der Mathematik bei diesem
Thema zu behandeln. Ersteres ist deshalb auch für den „Mathematiker“ interessant,
weil ohne ein Vertständnis dessen, was der Mediziner von einer
Computertomographie-Rekonstruktion
erwartet,
das
Aufstellen
eines
mathematischen Modells und dessen Lösung nicht sinnvoll und ohne Kenntnisse der
physikalischen Prozesse nicht möglich ist. Da es sich hierbei um eine Arbeit zu
einem PS für Lehramtskandidaten handelt, werden wir später auch Hinweise auf die
Möglichkeit der Bearbeitung dieses Themas im Unterricht und die dazu nötigen
Vereinfachungen eingehen.
Zu Beginn sei nun kurz auf die geschichtliche Entwicklung der Computertomographie
eingegangen. Nachdem es sich bei der CT (=Computertomographie) um ein
radiologisches Verfahren zur Erstellung von Schichtaufnahmen handelt, ist die
Entdeckung der Röngtenstrahlen im Jahr 1895 durch W.C. Röngten von
maßgeblicher Bedeutung. Einfache tomographische Techniken werden schon seit
langem in der Medizin verwendet. Anfang der 70 ger Jahre wurden dann die ersten
Computertomographen, als deren Erfinder G. Hounsfield und A. Cormack gelten,
verfügbar. Die mathematischen Grundlagen dazu lieferte der österreichische
Mathematiker Johann Radon bereits 1917.
Was steckt nun an Physik hinter der Funktionsweisen der Computertomographie?
Wie oben bereits erwähnt, ist die CT ein radiologisches Verfahren, eigentlich eine
Röngtenuntersuchung unter Zuhilfenahme eines Computers. Deshalb ist es wichtig,
Grundkenntnisse über die Röngtentechnik zu besitzen, um das Prinzip der CT zu
verstehen: Röngtenstrahlen druchdringen die meisten Stoffe, werden von ihnen aber
in unterschiedlichem Maß absorbiert oder zurückgeworfen. Die Intensität der
Absorbtion hängt mit der Dichte des jeweiligen Stoffes bzw. Körpers zusammen.
Röngtenstrahlen färben Photopapier schwarz, können aber auch mit Sensoren
gemessen werden. Eben diese Eigenschaften nützt die Computertomographie aus.
Je dichter ein Gewebe im Körper ist, desto schlechter läßt es Strahlen hindurch. So
kann man z.B. Knochen, Luft (in der Lunge), Wasseransammlungen und
Weichgewebe unterscheiden; denn die entstehenden Bilder sind wie ein S/W
Fernsehbild aus sehr vielen mehr oder weniger stark gefärbten Bildpunkten
aufgebaut, wobei der Schwärzungsgrad eines Punktes die bei dem entsprechenden
Punkt herrschende Dichte darstellt. Bei einer „normalen“ Röngtenuntersuchung
würde man nun allerdings ein zweidimensionales Bild erhalten, bei dem alle
hintereinanderliegenden Gewebe des Körpers als Schattenbild auf eine Ebene
projeziert sind und sich dort überlagern. Nicht so bei der Computertomographie .
Eine Tomographie bedeutet eine Darstellung in Schichten oder Scheiben, d.h. sie
1
25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
bildet das Körperinnere als einen Querschnitt ab, der sich überlagerungsfrei
betrachten läßt. Mit dieser Methode können auch sehr geringe Dichteunterschiede
erkennbar gemacht werden.
Dies bringt wesentliche Vorteile mit sich. So können z.B. die örtliche Lage , Form und
Größe von Organen bestimmt werden. und gesundes von krankem Gewebe
unterschieden werden, was vor allem bei Untersuchungen des Gehirns, des
Rückenmarks und der Wirbelsäule seine Anwendung findet. Im Speziellen z.B. bei
der Diagnose Gehirntumoren oder anderen Krebserkrankungen. Die Tomographie
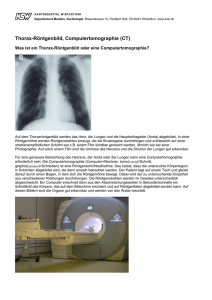
(siehe unten) ist für den Neurochirurgen sehr wichtig, um den Tumor genau zu orten,
damit eine allfällig notwendige Operation möglichst punktgenau durchführt werden
kann.
Computertomographie des
Computertomographie des
Computertomographie der
Schädels zur Beurteilung der Schädels zur Beurteilung der Lendenwirbelsäule, hier zwei
Hirnstrukturen
Knochenstrukturen
Schnitte in Höhe einer
("Weichteilfenster")
("Knochenfenster")
Bandscheibe
Wie funktioniert nun ein Computertomograph im Detail? (Bild siehe unten)
Im Inneren des Gerätes befindet sich eine Öffnung, in die der zu untersuchende
Patient auf einer Liege geschoben wird. (für jede einzelne Aufnahme fährt die Liege
mit dem Patienten einige Millimeter weiter und das Gerät durchleuchtet die nächste
Schicht des Körpers) Um die Öffnung wird eine Röngtenröhre kreisförmig d.h. um
die Längsachse des Patienten bewegt. Dabei werden (identische) Röngtenstrahlen
parallel durch den Körper gesendet (Fächer von Röngtenstrahlen) und die
Reststrahlung auf der gegenüberliegenden Seite gemessen. Dies geschieht durch
Detektoren, die gegenüber der Röngtenröhre montiert sind und genau registrieren,
wieviel Strahlung an welcher Stelle durch das Gewebe hindurch gegangen ist. Da mit
den daraus erhaltenen Angaben noch keine Bestimmung der Ortskoordinaten
möglich ist, wird das Objekt eben leicht gedreht und die Bestrahlung wiederholt. Dies
geschieht solange, bis eine Drehung um nahezu 180° erreicht ist (je mehr
Messungen durchgeführt werden, umso kleiner sind die minimalen Pixel des Bildes)
Der Computer errechnet nun die Differenz zwischen abgeschickter und empfangener
Intensität des Röngtenstrahls und setzt aus den Differenzwerten ein Bild zusammen,
dessen Grauwerte dabei der jeweiligen relativen Dichte des Gewebes entsprechen.
Ein solches Bild beruht auf der Untersuchung einer Körperscheibe.
Durch Aufeinanderlegen der einzelnen Schichtbilder ist es nun möglich, einen
dreidimensionalen Einblick z.B. in den menschlichen Kopf zu erhalten. Bei neueren ,
leistungsfähigen Spiral- CT rotiert die Röngtenstrahl-Detektor- Vorrichtung einmal pro
Sekunde um den in der Röhre liegenden Patienten. Dadurch entstehen innerhalb
kürzester Zeit sehr viele Schichtbilder, welche im Computer zu einem 3-D-Modell
zusammengesetzt werden können.
2
25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
Grundlage für die Berechnung der Ortskoordinaten aus den aus der RöngtenstrahlDetektor-Vorrichtung erhaltenen Daten führt uns nun zum mathematischen Teil der
Arbeit.
Sei I0 die Eingangsintensiät des Röngtenstrahls vor dem Durchgang durch den
Körper. Der Strahl durchquert den Körper geradlinig auf einer Strecke der Länge  x
und besitzt beim Austritt die Intensität I1. (mit u als Absorptionskoeffizienten). Das
Absorptionsgesetzt für Röngtenstrahlung besagt, dass
I1 = I0 .exp(   x )
Diese Gleichung ist nur für einen Körper mit konstantem Absorptionskoeffizienten
gültig. Bei einem inhomogenen Körper ist dieser Koeffizient im allgemeinen
ortsabhängig, so daß  ·  x durch ein Linienintegral ersetzt werden muss.


I 1  I 0    ( x ) d x 
 L

I0
 ln    ( x)d x
I1
Die Messungen von I0 und I1 liefern also Linienintegrale von  . Bestimmt man  (x)
aus der Gesamtheit aller Linienintegrale und stellt sie anschließend graphisch dar, so
erhält man das gesuchte Bild des Körpers. da man u eines Querschnitts bestimmen
will, reicht es aus, die Einschränkung von  auf die Querschnittsebene zu
betrachten. Der ortsabhängige Absorptionskoeffizient des Querschnitts kann also
durch eine zweidimensionale Absorptionsfunktion
 : IR2IR,
  L2
beschrieben werden. Die Funktion  läßt sich nun durch den Intensitätsverlust der
Röngtenstrahlung durch Absorption bei Durchleuchtung des Objekts aus vielen
verschiedenen Richtungen bestimmen. Wie vorher bereits festgehalten, wird das
objekt mit parallel ausgesandten Röngtenstrahlen durchstrahlt.
3
25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
Die Apparatur rotiere in n gleichverteilten Schritten zwischen  min und  max und
jedes Strahlenbündel bestehe aus nP gleichverteilten Strahlen zwischen Pmin und
Pmax (vgl. Abb.). Die Messungen mit dieser Geometrie liefern m:= n  nP Werte der
Linienintegrale
über die linearen Abschwächungskoeffizienten entlang der
Geradenstücke Mathematik fürs Leben am Beispiel der Computertomographie 7
Lj, j = 1,…,m, von den Quellen zu den Detektoren. Bezeichnen wir mit Quelle j und
Detektorj die durch das j-te Geradenstück Lj verbundenen Quellen und Detektoren,
j = 1,…,m, und mit I Quelle j bzw. I Detektor j die zugehörigen Intensitäten, so gilt:
IDetektor j  IQuelle j exp(-   ( x)dx).
Lj
Äquivalent dazu ist
IDetektor j
    ( x)dx
IQuelle j
Lj
Zur Rekonstruktion der linearen Abschwächungskoffizienten mÄussen wir das
Integralgleichungssystem
ln
  ( x)dx  b ,
j  1,..., m
j
Lj
lösen. Dabei sind die bj die experimentell ermittelten Werte:
IDetektor j
j
bj   ln
IQuelle j
Durch Streuung der Strahlung im Objekt sind die experimentell ermittelten Werte
in der Praxis allerdings noch mit einer Störung behaftet.
j  1,..., m ) ist die Radontransformation (vgl. [12])
Die Gleichung (   ( x)dx  bj ,
Lj
der Funktion  . Bei (geeignet gewählten) unendlich vielen Strahlen ist  eindeutig
durch die rechten Seiten bestimmt; bei endlich vielen Strahlen lässt sich  nur
approximativ bestimmen. Umkehrformeln sind zwar bekannt (vgl. zum Beispiel [11]),
jedoch für den mit diesem Projekt angesprochenen Schüler- und Studierendenkreis
ohne weitere Vorbereitung schwierig zu handhaben. Im nächsten Abschnitt stellen
wir
daher
eine
numerische
(approximative)
Lösung
von
j  1,..., m ) für endlich viele Strahlen vor, die für die Praxis
(   ( x)dx  bj ,
Lj
ausreichend genaue Näherungslösungen liefert.
4
25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
Neben der Diskretisierung der Umkehrformeln der Radontransformation (4) ergibt
sich eine andere Möglichkeit durch folgenden algebraischen Ansatz: Die Funktion 
  L2) beschreibt auf dem quadratischen Bildgebiet  2,
aus (  : IR2IR,
welches das zu rekonstruierende Objekt enthält, die Dichteverteilung der Materie. Auf
IR2\  2 soll verschwinden.
Mit Hilfe der Methode der finiten Elemente wollen wir eine Näherungslösung  des
Systems (   ( x)dx  bj ,
j  1,..., m ) berechnen. Dazu zerlegen wir das Quadrat
Lj
 2 in n2 gleich große quadratische Elemente, im Folgenden Pixel genannt. Wir
j  1,..., m im
suchen eine Bestapproximation an die Lösung von   ( x)dx  bj ,
Lj
n2-dimensionalen
Raum S = X 1,..., Xn 2 mit den Basisfunktionen xi: IR2IR, i=1,…n2:,
die durch
1, falls x im Pixel in der k  ten Zeile und l  ten Spalte der Zerleg ung liegt;
X ( k  1) n  l ( x)  
 0, sonst
(k, l=1,…,n) definiert sind. Die Funktionen Xi, i = 1,…,n2, sind also gerade die
Indikatorfunktionen für die n2 Pixel. Wir stellen die gesuchte Näherungslösung  als
Linearkombination der Basisfunktionen X1,…,Xn2 dar:
n2
 (x)=  uiXi ( x )
i 1
Approximation des Objekts durch endlichdimensionalen Teilraum.
Bei dieser Wahl des Raumes S ist  in jedem Pixel der Zerlegung konstant und
 | IR 2\  2  0. Das Bild, welches der Mediziner später für seine Diagonse verwendet,
entsteht durch Darstellung des Wertes im i-ten Pixel (also von ui) als Grauwert. Die
Diskretisierung ist also dem Problem angepasst. In der Praxis sind zur Zeit
Auflösungen von 512 x 512 Pixel gängig. Eingesetzt in (4) ergibt sich für i = 1,…,m
5
25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
kann man (6) als lineares Gleichungssystem
Au = b
mit dem unbekannten Koeffizientenvektor u und den gemessenen Werten der
rechten Seite b schreiben. Die Formel für aij besagt, dass das (i; j)-te Element von A
gerade die Länge des Schnitts des i-ten Strahls mit dem j-ten Pixel ist.
Die Zahl der Messungen (d. h. die Zahl der Gleichungen im linearen Gleichungssystem) wird gewöhnlich wesentlich größer sein als die Anzahl der Pixel, um
die Qualität der Rekonstruktion zu erhöhen. Somit ergibt sich ein überbestimmtes
Tabelle 1: Werte für die Rekonstruktion. In der Spalte nnz(A) ist der Anteil der von Null verschiedenen Elemente in A, in der
letzten Spalte der Speicheraufwand in Megabyte angegeben.
lineares Gleichungssystem sehr großer Dimension m x n2, dessen
Koeffizientenmatrix A aber schwach besetzt ist, d.h. nur wenige Einträge von A sind
von Null verschieden, vgl. Abb. 6 und Tab. 1. Es gilt die folgende Abschätzung:
6
25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
Satz 1:
In einer Zeile der Matrix A sind höchstens 2n-1 Elemente von Null verschieden.
Diese Aussage folgt durch einfache geometrische Überlegungen, die am Besten an
Hand von Skizzen nachzuvollziehen sind.
Wegen der großen Dimension von A ist eine direkte Lösung von (8) - etwa mit Hilfe
von Gauß-Elimination (bzw. Cholesky-Zerlegung) oder QR-Zerlegung (vgl. [6]) – des
Minimierungsproblems nicht mehr effizient möglich. Die Ursache dafür liegt darin,
dass die berechnete Zerlegung nicht mehr dünn besetzt ist. Der Rechenaufwand für
die direkte Lösung liegt in der Größenordnung n6, wenn mit einer Auflösung von n x n
Pixeln gerechnet wird. Bei n = 512 wird diese Berechnung selbst auf den immer
schneller werdenden Computern auch in naher Zukunft nicht in vernünftiger Zeit
möglich sein. Der Speicheraufwand ist mit 8n4 Bytes ebenfalls inakzeptabel hoch: Bei
optimaler Programmierung würde die Lösung auf einem Rechner mit einer
Taktfrequenz von 2 GHz und mindestens 550 GB Hauptspeicher mehr als einen
Monat dauern. Eine effiziente Lösung muss daher iterative Verfahren wie das
Verfahren des steilsten Abstiegs, das Verfahren der konjugierten Gradienten (cgVerfahren) oder das Kaczmarz-Verfahren verwenden. Prinzipiell eignen sich alle
Verfahren, bei denen die Matrix A nur in Form von Matrix-Vektor Produkten eingeht,
also wo nur Au und ggf. ATv für Vektoren u und v berechnet werden müssen. Hierfür
müssen nämlich nur die von Null verschiedenen Einträge von A gespeichert werden,
was sich mit dem in Tabelle 1 aufgeführten Speicherbedarf realisieren lässt. Zum
Vergleich: Für n = 512 sind für die Speicherung von A nur 1:7 GB, für ATA jedoch
550 GB erforderlich. Die Idee des Verfahrens der konjugierten Gradienten zur
Lösung eines linearen Gleichungssystems ~ ~
~
Mu = g,
M  IR n , n , g  IR n
mit symmetrischer und positiv definiter Matrix M besteht darin, das Minimum der
~
quadratischen Funktion ||g-Mu||2 nicht im gesamten hochdimensionalen Raum IR n
sondern nur im niedrigdimensionalen affinen Teilraum Kk(M, g) = u(0) +
Span{g,Mg,M2gm,…,Mk-1g},
Mathematik
fürs
Leben
am
Beispiel
der
Computertomographie 11 dem verschobenen k-ten Krylov-Raum bzgl. M und g, zu
bestimmen. Man kann zeigen, dass dies möglich ist, indem man in jedem Teilschritt
nur ein eindimensionales Minimierungsproblem löst. Details hierzu findet man in den
meisten Numerik-Lehrbüchern.
~  n2. Eine Variante des cgIn unserem Fall ist M = ATA, g = AT b und n
Verfahren angewandt auf die Normalengleichungen ist das cgls-Verfahren. Ein
Pseudo-Code hierfür ist in Algorithmus 1 angegeben. Die wichtigsten Eigenschaften
des cgls-Verfahrens sind im folgenden Satz zusammengefasst.
Satz 2
Die k-te Iterierte des cgls-Verfahrens liegt im verschobenen Krylov-Raum
u(k)  u(0) + Kk(AT A;AT r(0))
= u(0) + Span{AT r(0), (ATA)AT r(0); : : : ; (ATA)k-1AT r(0)},
wobei r(0) = b - Au(0) das Anfangsresiduum ist. Unter allen Elementen u dieses affinen
Raumes minimiert u(k) die Residuennorm ||b – Au||.
7
25.02.2003
Michaela Erber
Angela Rottermanner
Computertomographie
Das cgls-Verfahren berechnet zwar theoretisch die exakte Lösung nach höchstens n 2
Schritten, jedoch ist dieses Resultat für die Praxis aus verschiedenen Gründen
irrelevant. Zum einen ist das Gleichungssystem selbst bereits durch diverse
Näherungen konstruiert worden (vor allem durch die Diskretisierung in Pixel und die
Annahme, dass in jedem dieser Pixel die Dichte konstant ist). Zum anderen wäre der
Aufwand für n2 Schritte des Iterationsverfahrens mit dem eines direkten Verfahrens
vergleichbar und daher inakzeptabel. Schlie¼lich ist Satz 2 nur bei exakter
Rechnung, d.h. ohne Berücksichtigung von Rundefehlern, richtig. Die Bedeutung des
Verfahrens der konjugierten Gradienten liegt darin, dass es häufig schon nach
wenigen Schritten brauchbare Näherungen berechnet, nämlich solche, deren Fehler
n der Größenordnung des Diskretisierungsfehlers liegen. Wie wir später bei den
numerischen Ergebnissen sehen werden, genügen für das CT-Problem tatsächlich
weniger als 10 Schritte; die Lösung kann damit innerhalb von Sekunden berechnet
werden (im Vergleich zu einem Monat bei direkter Lösung).
Der Genauigkeit der Rekonstruktion sind neben der Lösung des linearen
Gleichungssystems und der Auflösung bei der Ortsdiskretisierung auch physikalische
Grenzen gesetzt: Die maximale Auflösung von Feinstrukturen ist bereits durch die
Dicke des Strahlenbündels limitiert. Innerhalb eines Elementquaders kann das
Schwächungsvermögen der Materie nicht differenziert werden. Jeder errechnete
lokale Schwachungskoeffizient stellt somit einen Mittelwert der Schwächung in seiner
quaderförmigen Umgebung dar.
Nachdem diese Arbeit im Rahmen einer LVA für Lehramtskandidaten verfaßt wird,
haben wir uns auch damit beschäftigt, wie dieses Thema in der Schule umgesetzt
werden könnte. Der vorhin vorgestellte algebraische Zugang basiert nach einigen
Vereinfachungen auf dem Schulstoff der Mittelstufe. So ist es z.B. möglich, bzw. es
genügt, zur Berechnung der Matrix aus der Diskretisierung, Geradengleichungen in
der Ebene aufzustellen und Schnittpunkte von Geraden zu berechnen. Bei der
Diskretisierung kann ggf. die Exponentialfunktion durch eine Potenzfunktion, sowie
das Integral durch eine Riemannsumme ersetzt werden. Falls der Wunsch nach einer
Vertiefung besteht, die über den Schulstoff hinausgeht, bestehen folgende
Möglichkeiten z.B. Einführung überbestimmter Gleichungssysteme, bei denen es im
Allgemeinen keine Lösung gibt- Formulierung als Ausgleichsproblem. oder aber auch
Notwendigkeit von Näherungsverfahren unter Berücksichtigung des Rechen- und
Speicheraufwandes.
8