Kombinatorische Techniken
Werbung
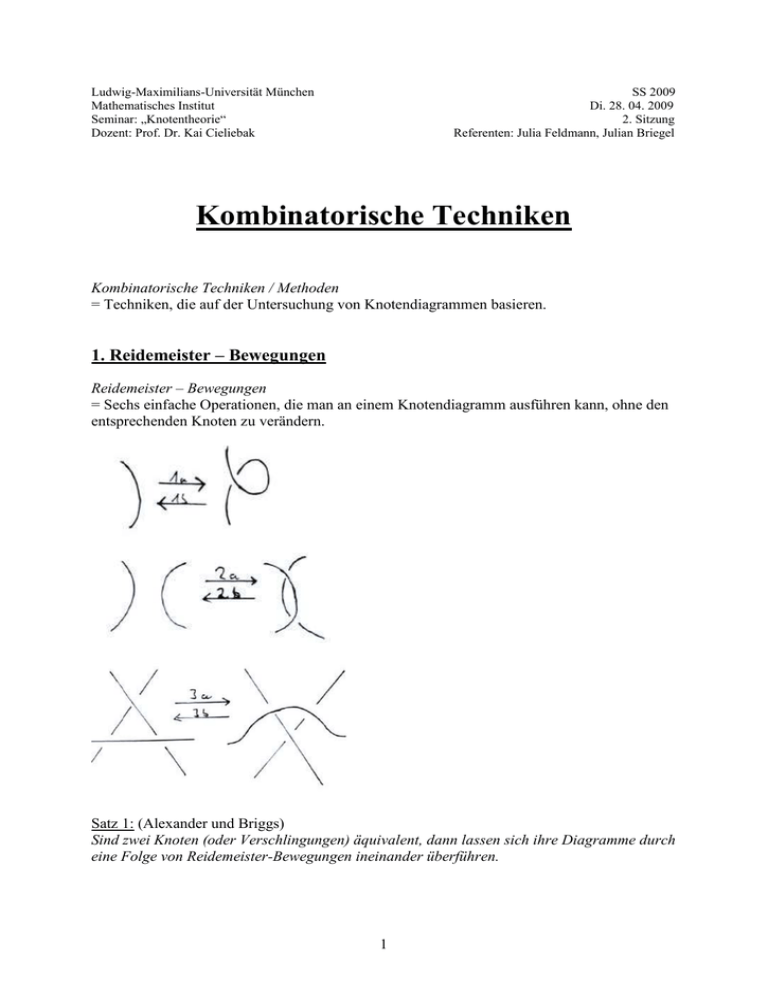
Ludwig-Maximilians-Universität München Mathematisches Institut Seminar: „Knotentheorie“ Dozent: Prof. Dr. Kai Cieliebak SS 2009 Di. 28. 04. 2009 2. Sitzung Referenten: Julia Feldmann, Julian Briegel Kombinatorische Techniken Kombinatorische Techniken / Methoden = Techniken, die auf der Untersuchung von Knotendiagrammen basieren. 1. Reidemeister – Bewegungen Reidemeister – Bewegungen = Sechs einfache Operationen, die man an einem Knotendiagramm ausführen kann, ohne den entsprechenden Knoten zu verändern. Satz 1: (Alexander und Briggs) Sind zwei Knoten (oder Verschlingungen) äquivalent, dann lassen sich ihre Diagramme durch eine Folge von Reidemeister-Bewegungen ineinander überführen. 1 Beweis: Seien K und J zwei äquivalente Knoten mit regulären Projektionen, dann hängen K und J über eine Folge von Knoten zusammen, von denen jeder aus dem vorigen durch eine elementare Deformation hervorgeht. (Evtl. muss man sicherstellen, dass jeder dieser Knoten eine reguläre Projektion besitzt. Dies gilt jedoch, da die Anwendung einer kleinen Drehung einen äquivalenten Knoten liefert, der eine reguläre Projektion besitzt. Gegebenenfalls muss man eine Drehung anwenden um auch nach der Projektion des Dreiecks, an dem entlang die elementare Deformation durchgeführt wird, ein Dreieck in der Ebene zu erhalten.) Das Bild zeigt die Situation, in der der Knoten gedreht werden muss, weil das Dreieck durch die Projektion in zRichtung auf eine Gerade abgebildet wird. Es genügt also, den Fall zu betrachten, in dem die beiden Knoten über eine einzige elementare Deformation zusammenhängen. Innerhalb des Dreiecks der elementaren Deformation können sich viele Segmente oder Kreuzungen des Knotendiagramms befinden. Es lässt sich jedoch in viele kleine Dreiecke unterteilen, von denen jedes nur höchstens eine Kreuzung enthält. Mittels dieser Unterteilung kann man die eine elementare Deformation durch eine Folge vieler kleiner Deformationen beschreiben. Hier ist jetzt eine Fallunterscheidung notwendig: a) Kein anderer Teil des Knotens wird bei der elementaren Transformation überquert. In diesem Fall gilt sofort, dass die Diagramme gleich sind. 2 b) Ein anliegendes Segment wird gekreuzt. In diesem Fall überführt eine Reidemeisterbewegung vom Typ 1 die Diagramme ineinander. c) Ein anderes Segment wird gekreuzt. In diesem Fall überführt eine Reidemeisterbewegung vom Typ 2 die Diagramme ineinander. d) Eine Kreuzung wird überquert. In diesem Fall überführt eine Reidemeisterbewegung vom Typ 3 die Diagramme ineinander. In jedem Fall überführt also eine Reidemeisterbewegung die Diagramme ineinander. Beispiele: 1) Zeigen Sie, dass folgende Änderung mittels zweier aufeinanderfolgender Reidemeister-Bewegungen erreicht werden kann. 3 2) Suchen Sie eine Folge von Reidemeister-Bewegungen, die das Diagramm des Unknotens in die Standardform überführen. 2. Färbungen Ralph Fox: Färbbarkeit = Methode, Knoten zu unterscheiden. Ein Knotendiagramm ist färbbar, wenn jeder Bogen mit einer von drei Farben – Rot, Grün, Blau – gekennzeichnet werden kann derart, dass 1) mindestens zwei verschiedene Farben benutzt werden 2) an einer Kreuzung, an der zwei Farben vorkommen, alle drei Farben vorkommen Satz 2: Wenn irgendein Diagramm eines Knotens K färbbar ist, dann ist jedes Diagramm von K färbbar. Beweis: Aufgrund von Satz 1 sind die Diagramme eines Knotens bis auf Reidemeisterbewegungen identisch. Es genügt zu zeigen, dass nach Ausführen einer Reidemeister-Bewegung an einem färbbaren Knotendiagramm das resultierende Diagramm wieder färbbar ist. Der Beweis zerfällt also in sechs Teilschritte – entsprechend der sechs Reidemeister-Bewegungen. Es sind nur die für die Veränderung der Färbung relevanten Teile des Knotens zu beachten. Die Kontaktstellen zum restlichen Knoten verändern sich jedoch nicht und die Farben des restlichen Diagramms bleiben so, wie sie ursprünglich waren. 4 Alle Anforderungen an Färbbarkeit sind noch erfüllt. Mann nennt einen Knoten färbbar, wenn seine Diagramme färbbar sind. 5 Es gibt nichttriviale Knoten! Der triviale Knoten ist nicht färbbar, da seine Standardprojektion nicht färbbar ist! Jeder färbbarer Knoten ist nicht trivial! Es gibt auch Kreuzungen mit nur einer Farbe! Es gibt unendlich viele verschiedene Knoten. o Mittels Induktion kann man zeigen, dass der n-Kleeblattknoten genau 3*2n Färbungen hat. Beispiel: Die Knoten 31, 61, 74 und 77 sind färbbar. Die Verschlingungszahl einer orientierten Verschlingung zweier Komponenten J und K: Jedem Kreuzungspunkt in einem Diagramm lässt sich ein Vorzeichen zuordnen: + 1 für eine rechtshändige Kreuzung - 1 für eine linkshändige Kreuzung +1 -1 Die Verschlingungszahl lk(K, J) („link“) von K und J ist die durch 2 geteilte Summe der Vorzeichen aller Kreuzungspunkte, an denen K und J zusammentreffen. (Nicht betrachtet werden Kreuzungen an denen K oder J sich selbst kreuzen.) Beispiel: Berechnung der Verschlingungszahl der Whitehead-Verschlingung: 0 6 Die triviale Verschlingung zweier Komponenten ist färbbar. (mit allen drei Farben, mit genau zwei Farben) Eine nicht färbbare Verschlingung kann nicht trivial sein. Beispiel: Whitehead-Verschlingung 3. Eine Verallgemeinerung der Färbbarkeit: Etikettierungen modulo p Statt 3 Farben: Zahlen: 0 – 1 – 2 Färbbarkeit Beziehung: Wenn der überkreuzende Bogen mit x und die beiden anderen Bögen mit y und z etikettiert werden, dann ist die Differenz 2x – y –z durch 3 teilbar. 2x – y – z = 0 (mod 3) Ein Knotendiagramm lässt sich etikettieren modulo p (mod p), wenn jede Kante mit einer ganzen Zahl zwischen 0 und p – 1 (ihrem Etikett) versehen werden kann derart, dass 1) an jeder Kreuzung die Beziehung 2x – y – z = 0 (mod p) erfüllt ist, wobei x das Etikett der Überkreuzung ist und y und z die beiden anderen Etiketten sind 2) mindestens zwei Etiketten verschieden sind. Die möglichen Werte für p werden auf die ungeraden Primzahlen eingeschränkt. Grund dafür, nicht alle Zahlen zuzulassen, ist das Ziel der Unterscheidbarkeit von Knoten durch die Etikettierung mit möglichst wenigen Zahlen. Satz 3: (Etikettierungssatz) Wenn irgendein Diagramm eines Knotens eine Etikettierung mod p erlaubt, dann besitzt jedes Diagramm dieses Knotens eine Etikettierung mod p. Beweis: Wie bei der Färbbarkeit, genügt es zu zeigen, dass nach Ausführen einer Reidemeister-Bewegung an einem etikettierten Knotendiagramm das resultierende Diagramm wieder etikettierbar ist: 7 Beispiel: Beispiel: Die Knoten 41 und 51 können mod 5 etikettiert werden. Beispiel: Mit Hilfe von Etikettierungen z.B. mod 5 und mod 7, kann man zeigen, dass die Knoten 41, 71 und 816 verschieden sind: 41: mod 5, aber nicht mod 7 71: mod 7, aber nicht mod 5 816: sowohl mod 5 als auch mod 7 8 4. Matrizen, Etikettierungen und Determinanten Vereinfachung durch Algebraisierung: Jeder Bogen eines vorgegebenen Diagramms wird mit einer Variablen xi etikettiert. An jeder Kreuzung fordert die Definition eine Relation zwischen den Variablen: Wenn der Bogen xi die Bögen xj und xk überkreuzt, dann soll gelten: 2xi – xj – xk = 0 (mod p) Ein Knotendiagram kann mod p etikettiert werden, wenn dieser Satz von Gleichungen eine Lösung mod p besitzt, bei der nicht alle xi gleich sind. Lineare Algebra: Lösung eines linearen Gleichungssystems Matrizen (Wenn p eine Primzahl ist, bilden die ganzen Zahlen mod p einen Körper.) xi = 1 für alle i ist eine Lösung des Gleichungssystems. Die Summe zweier Lösungen ist wieder eine Lösung. Wenn es eine Lösung gibt, bei der nicht alle Einträge gleich sind, gibt es auch eine Lösung mit irgendeinem xj = 0 [z.B. 41 und p = 5: aus x1 = 3, x2 = 4, x3 = 2, x4 = 1 wird x1 = 2, x2 = 3, x3 = 1, x4 = 0] Eine nichttriviale Lösung mit irgendeinem xj = 0 definiert eine Etikettierung des Knotens. Somit gibt es also zu einer Lösung, bei der nicht alle xi gleich sind, eine entsprechende nichttriviale Lösung des durch die ursprüngliche Matrix ohne die j-te Spalte gegebenen Gleichungssystems. Bei einer Quadratischen Matrix, die wir haben, folgt jede einzelne Gleichung aus den übrigen. Sie bedingen sich also alle gegenseitig. Die Multiplikation gewisser Zeilen mit – 1 führt zu einer Matrix, deren Zeilen sich zu Null addieren. (Nur nötig, wenn dies nicht bereits der Fall ist, wenn also ein Bogen mehrere andere Bögen überkreuzt) Dann den Algorithmus anwenden: Man orientiere den Knoten. An jeder Kreuzung im Diagramm markiere man einen Punkt rechts neben dem überkreuzenden Bogen direkt vor dem Kreuzungspunkt. Jetzt zähle man die Bögen des Diagramms, die ein Pfad kreuzt, der diesen Punkt mit einem – vom Diagramm weit entfernten – Punkt in der Ebene verbindet. Kreuzt er eine ungerade Zahl von Bögen, so multipliziere man die entsprechende Zeile der Matrix mit – 1. Summe der Zeilen = 0 Daraus ergibt sich folgender Satz: Satz 4: Ein Knotendiagramm mit n Bögen definiert eine n x n – Matrix. Man betrachte die durch Streichen einer beliebigen Zeile und einer beliebigen Spalte entstehende Matrix. Der Knoten kann genau dann mod p etikettiert werden, wenn das dieser Matrix entsprechende Gleichungssystem eine nichttriviale Lösung mod p besitzt. 9 Die Determinante zeigt an, ob es eine nichttriviale Lösung gibt: o Det = 0 (mod p) => eine Lösung existiert o Zahl der Lösungen ist abhängig vom Rangdefekt mod p der Matrix Rangdefekt = Dim Kern (Matrix) Rangdefekt = die Anzahl der Nullen in der Diagonalen (oder der durch p teilbaren Einträge bei Rechnung mod p) Jede quadratische Matrix lässt sich mittels (hier: ganzzahliger) Zeilen- und Spaltenumformungen diagonalisieren Als Determinante eines Knoten bezeichnet man den Betrag der Determinante der durch Streichen einer Zeile und einer Spalte konstruierten assoziierten (n – 1) x (n – 1) -Matrix. Den Rangdefekt mod p der durch Streichen einer Zeile und einer Spalte konstruierten assoziierten (n – 1) x (n – 1) -Matrix eines Knotens nennt man den Rang mod p des Knotens. Satz 5: Die Determinante eines Knotens und sein Rang mod p sind unabhängig von der Wahl des Diagramms und der Etikettierung. Beweis: Der Beweis besteht aus zwei Teilen: 1) Wenn bei einer quadratischen Matrix die Summe der Zeilen und die der Spalten null ergibt, dann hängt der Rangdefekt (und der Betrag der Determinante) derjenigen Matrix, die durch Streichen einer Zeile und einer Spalte entsteht, nicht davon ab, welche Zeile und welche Spalte gestrichen wurde. (lineare Algebra) Außerdem hat das Hinzufügen einer neuen Spalte und Zeile, die beider außer einer 1 in der Diagonalen ansonsten nur Nullen enthalten, keinen Einfluss auf den Rangdefekt und die Determinante der Matrix. 2) Der Einfluss der Reidemeister-Bewegungen: Die Reidemeister-Bewegung vom Typ 2a z. B. führt zu zwei weiteren Zeilen und Spalten. Zwei der neuen spalten ergeben sich durch Aufspalten eines der alten Bögen in zwei Bögen, und somit sind die Einträge der Summe dieser zwei Spalten durch die alte Spalte festgelegt. Ein paar Zeilen- und Spaltenumformungen zeigen, dass die neue Matrix in die alte Matrix mit zwei hinzugefügten Zeilen und Spalten, von denen jede eine einzigen ±1 enthält, umgeformt werden kann. Beispiel: Bestimmen Sie für den Knoten 62 die assoziierte Matrix und deren Determinante. Untersuchen Sie, für welches p eine Etikettierung mod p möglich ist. Dieser Knoten ist für p = 11 etikettierbar, da die Determinante des Knotens = 0 mod 11 ist. 5. Das Alexander-Polynom Einträge der Matrix: Polynome Zur Bildung des Alexander-Polynom AK (t) eines Knotens K: Orientiertes Diagramm für K Nummerierte Bögen und Kreuzungen n x n – Matrix (n Bögen, n Kreuzungen) o Kreuzung l ist rechtshändig (Bogen i verläuft oberhalb der Bögen j und k): 1 – t in i-te Spalte der l-ten Zeile -1 in j-te Spalte t in k-te Spalte 10 o Kreuzung l ist linkshändig (Bogen i verläuft oberhalb der Bögen j und k): 1 – t in i-te Spalte der l-ten Zeile t in j-te Spalte -1 in k-te Spalte o alle übrigen Spalten der l-ten Zeile sind 0 t 1-t k 1-t -1 k i j -1 t j i Die aus der gerade beschriebenen n x n – Matrix durch Streichen der letzten Zeile und Spalte gebildete (n-1) x (n-1) – Matrix nennt man eine Alexander-Matrix des Knotens K. Die Determinante der Alexander-Matrix heißt Alexander-Polynom von K. (Die Determinante einer 0 x 0 – Matrix wird als 1 definiert.) Satz 6: Wählt man bei der Berechnung des Alexander-Polynoms eines Knotens zwei unterschiedliche Diagramme oder Etikettierungen, dann unterscheiden sich die zwei Polynome um einen Faktor ± tk, wobei k ganzzahlig ist. 11 Beispiel: Literatur: C. LIVINGSTON, „Knotentheorie für Einsteiger“, Vieweg 1995. D. HELMS, „Kombinatorische Techniken in der Knotentheorie“, aus: Prof. Dr. J. Lohkamp, Priv. Doz. Dr. A. Dessai, Seminar zur Topologie (Knotentheorie), WS 03/04, Universität Augsburg zu finden unter: http://www.math.uni-augsburg.de/geo/lehre/WS03/Kombinatorische_Techniken.pdf 12