Uebungausfgaben_Benford

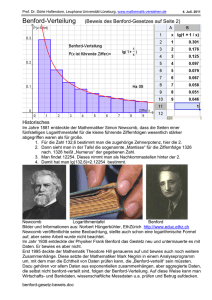
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
Aufgabe 1)
Benford Verteilung
Nach dem Benford Gesetz gilt: Die Wahrscheinlichkeit, dass eine Zahl mit der Ziffer
n beginnt, ist:
P( X  n)  log 10(1  1n )
Demnach ergeben sich für die Ziffern 1 bis 9 folgende Wahrscheinlichkeiten:
erste Ziffer
n
Wahrscheinlichkeit
für erste Ziffer
P(X=n)
1
2
3
4
5
6
7
8
9
0,301
0,176
0,125
0,097
0,079
0,067
0,058
0,051
0,046
a) Beschreiben Sie die beiden Eigenschaften von diskreten Verteilungen und in
welchen drei Formen lassen sich diskrete Verteilungen darstellen?
b) Zeigen Sie anhand der Eigenschaften, dass es sich bei der obigen Tabelle um
eine Verteilung handelt!
c) Stellen Sie sowohl die Wahrscheinlichkeitsverteilung der Zufallsgröße als auch
die kumulierte Wahrscheinlichkeitsverteilung tabellarisch und grafisch im TIVoyage 200 dar!
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
Aufgabe 2)
Das Gesetz der großen Zahlen
a) Der untenstehenden Tabelle kann man entnehmen, wie häufig bei den
Ländergrößen die erste Ziffer gleich n ist. Dabei haben wir einmal nach
alphabetischer Reihenfolge die ersten 50 Länder analysiert und ein weiteres Mal die
absoluten Häufigkeiten bei allen 193 Ländern beobachtet. Berechnen Sie zuerst die
relativen Häufigkeiten beider Versuchsreihen.
absolute
Häufigkeit
relative
Häufigkeit
absolute
Häufigkeit
relative
Häufigkeit
bei 50
Ländern
bei 193
Ländern
54
bei 193
Ländern
1
bei 50
Ländern
11
2
13
39
0,17609126
3
5
23
0,12493874
4
7
20
0,09691001
5
5
14
0,07918125
6
3
13
0,06694679
7
3
12
0,05799195
8
2
8
0,05115252
9
1
10
0,04575749
Summe
50
193
1
erste Ziffer
n
BenfordVerteilung
0,30103
b) Stellen Sie die relativen Häufigkeiten grafisch im TI-Voyage 200 in zwei
Koordinatensystemen dar. Vergleichen Sie die beiden Grafiken mit denen der
Benford Verteilung. Dazu sollen die Wahrscheinlichkeiten der ersten Ziffer nach dem
Benford Gesetz zusätzlich in die beiden Koordinatensysteme gezeichnet werden.
c) Die nachstehende Abbildung bezieht sich auf ein Zufallsexperiment, bei dem
ganze Zufallszahlen im Intervall [1;9] gezogen wurden. Die Anzahl der Zufallszahlen
wurde bei jedem Versuch von anfangs 10 bis auf 2000 erhöht. Durch das Betrachten
der relativen Häufigkeiten einer Zahl, z.B. der „6“, in Abhängigkeit von der Anzahl der
erzeugten Zahlen, ergab sich folgende Grafik:
y
0.25
0.2
0.15
0.1
0.05
0
0
500
1000
1500
2000
x
Erklären Sie an diesem Beispiel, was das „Gesetz der großen Zahlen“ aussagt!
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
Aufgabe 3)
Binomialverteilung
Sie sind bei der Zifex GmbH in der Innenrevision beschäftigt. Dort überprüfen Sie
Einkaufsrechnungen. Dabei stellen Sie fest, dass bei den insgesamt 250 Zahlen auf
den Rechnungen 32 Zahlen mit der Ziffer „4“ beginnen.
a) Kann man bei der Aneinanderreihung der obigen 250 Zufallsexperimente von
einer Bernoulli-Kette sprechen? Welche Voraussetzungen müssen dafür erfüllt
sein?
b) Wie groß ist die Wahrscheinlichkeit, dass von den insgesamt 250 Zahlen in
den Rechnungen 32 Zahlen mit der Ziffer „4“ beginnen, wenn das
Datenmaterial dem Benford Gesetz unterliegt?
c) Mit
welcher
Wahrscheinlichkeit
hat
ein
250
Zahlen
umfassendes
Datenmaterial bei weniger als 32 Zahlen eine „4“ als Anfangsziffer? Wie hoch
ist die Irrtumswahrscheinlichkeit, wenn man bei dem obigen Beispiel der
Einkaufsrechnungen behauptet, dass die Daten manipuliert sind.
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
Aufgabe 4)
Chi-Quadrat-Test für Verteilungen
Überprüfe mit Hilfe des
 2  Tests , ob sich die Benford Verteilung und die Verteilung
der ersten Ziffer bei den Länderflächen signifikant unterscheiden. Hierfür kann man
in der mittleren Spalte der nachstehenden Tabelle die absoluten Häufigkeiten der
ersten Ziffer bei insgesamt 50 Ländern entnehmen. In der rechten Spalte stehen die
Wahrscheinlichkeiten für die erste Ziffer nach der theoretischen Benford Verteilung.
erste Ziffer
absolute
Häufigkeit
Benford
Verteilung
i
für n=50
P(X=i)=pi
1
2
3
4
5
6
7
8
9
11
13
5
7
5
3
3
2
1
0,3010
0,1761
0,1249
0,0969
0,0792
0,0669
0,0580
0,0512
0,0458
Unterscheiden sich diese beiden Verteilungen signifikant?
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
Lösung zu Aufgabe 1)
a) Die Wahrscheinlichkeitsfunktion einer Zufallsgröße X besitzt die folgenden
Eigenschaften:
● Wenn man alle möglichen Ausprägungen xi der Zufallsvariablen X betrachtet
und deren Wahrscheinlichkeiten addiert, folgt die Eigenschaft, dass die
Summe der Wahrscheinlichkeiten aller Ausprägungen einer Zufallsvariablen
gleich 1 ist:
f
X
( xi )  1
i
● Des Weiteren ergibt sich aus der Definition der Wahrscheinlichkeit die weitere
Eigenschaft, dass alle Eintrittswahrscheinlichkeiten zwischen 0 und 1 liegen:
0  fX ( xi )  1
Eine diskrete Verteilung lässt sich in drei Formen darstellen:
● (1) eine vollständige Liste ( xi, P( X  xi )) [Tabelle in der Aufgabenstellung)
● (2) eine Formel; die Wahrscheinlichkeitsfunktion fX ( xi ) [Formel in der
Aufgabenstellung]
● (3) ein Histogramm bei diskreten Verteilungen; eine Kurve (genannt
Wahrscheinlichkeitsdichtefunktion) bei stetigen Verteilungen.
b) Aus der Tabelle ist ersichtlich, dass die Wahrscheinlichkeiten für die einzelnen
Ziffern im Intervall [0;1] liegen. Weiterhin ergibt sich durch das Aufsummieren der 9
Wahrscheinlichkeiten die Summe 1. Damit sind die beiden Eigenschaften erfüllt.
c)
Darstellung
der
Wahrscheinlichkeitsverteilung
und
der
Wahrscheinlichkeitsverteilung im TI-Voyage 200 in tabellarischer Form:
Säulendiagramm für P( X  n)
und
P( X  n) :
kumulierten
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
zu Aufgabe 2)
a)
erste Ziffer
n
1
2
3
4
5
6
7
8
9
Summe
absolute
Häufigkeit
für n=50
11
13
5
7
5
3
3
2
1
50
b)
relative
Häufigkeit
für n=50
0,22
0,26
0,1
0,14
0,1
0,06
0,06
0,04
0,02
1
absolute
Häufigkeit
für n=193
54
39
23
20
14
13
12
8
10
193
relative
Häufigkeit
für n=193
0,27979275
0,20207254
0,11917098
0,10362694
0,07253886
0,06735751
0,06217617
0,04145078
0,05181347
1
BenfordVerteilung
n->∞
0,30103
0,17609126
0,12493874
0,09691001
0,07918125
0,06694679
0,05799195
0,05115252
0,04575749
1
für n=50:
für n=193:
c) Die relative Häufigkeit hn( X  6) für das Auftreten des Ereignisses „Die Zahl ist 6“
nähert sich beliebig nah der Wahrscheinlichkeit P( X  6)  P(6) für dieses
Ereignis, wenn man nur die Anzahl n der Versuche, bei denen das Ereignis auftreten
kann, beliebig groß macht. Betrachten wir weiterhin das obige Zufallsexperiment, in
dem ganze Zufallszahlen von 1 bis 9 erzeugt werden, und interessieren uns für die
Häufigkeit einer Ziffer, lässt sich am Beispiel der Zahl „6“ sagen: Die relativen
Häufigkeiten
hn( X  6)
stabilisieren
Vorgangsrealisierungen gegen den Wert
sich
1
9
.
mit
wachsender
Anzahl
n
von
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
zu Aufgabe 3)
a) Voraussetzung für einen Bernoulliversuch:
● Es liegt eine Bernoulli-Kette der Länge n vor. (Hier ist n=250)
● Das zugehörige (einstufige) Zufallsexperiment muss ein Ja/Nein-Versuch
sein. Es dürfen nur zwei Ereignisse möglich sein. (Hier sind nur die beiden
Ereignisse „Erste Ziffer ist gleich 4“ und „Erste Ziffer ist ungleich 4“
möglich.)
● Die Erfolgswahrscheinlichkeit p für P(Y=4) muss in jeder Stufe der BernoulliKette gleich sein. Hier ist P (Y  4)  log 10(1  14 )  0,0969
● Die Gegenwahrscheinlichkeit q für P(Y=“Die erste Ziffer ist ungleich 4“) ist
q=1-p. (Hier: q=0,9031)
Die Zufallsgröße X, welche die Werte 0;1;2;…;n mit den Wahrscheinlichkeiten
P( X  k )  Bn; p; k  ( kn) * p k * (1  p)nk
annimmt, heißt binomialverteilt mit den Parametern n und p. Die zu X gehörende
Wahrscheinlichkeitsverteilung nennt man Binomialverteilung.
Somit liegt eine Bernoulli-Kette vor.
b) Gegeben sind die Werte:
n  250;
p  log 10(1  14 )  0,0969; k  32
Diese werden in der Formel der Binomialverteilung eingesetzt:
P( X  32)  B 250; 0, 0969; 32  ( 250
) * 0,096932 * (1  0,0969) 25032
32
Dies lässt sich mit dem TI-Voyage 200 folgendermaßen berechnen:
Die Wahrscheinlichkeit, dass bei einem 250 Zahlen umfassten Datenmaterial,
welches dem Benford Gesetz unterliegt, insgesamt 32 Mal die „4“ Anfangsziffer ist,
beträgt etwa 2,12%.
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
c) Betrachten der kumulierten Wahrscheinlichkeitsfunktion:
31
P( X  31)   ( 250
) * 0,096931 * (1  0.0969) 25031
31
i 0
Berechnen mit dem TI-Voyage 200:
Bei 250 Zahlen beginnen zu etwa 93,6% weniger als 32 Zahlen mit einer „4“. Bei der
Behauptung „Die Daten sind manipuliert, denn die Wahrscheinlichkeit für eine „4“ ist
höher als 9,69%!“ beträgt die Irrtumswahrscheinlichkeit 6,4%.
Übungsaufgaben -Benford Gesetz__________________________________________________________________________________________
zu Aufgabe 4)
Bei dem Chi-Quadrat-Test auf die Benford Verteilung ergibt sich folgender ChiQuadrat-Wert (gelb markiert):
erste
Ziffer
absolute
Benford
Häufigkeit Verteilung
Hn ( X  i )  n * pi
i
für n=50
P(X=i)=pi
n*pi
=delta
delta^2/(n*pi)
1
2
3
4
5
6
7
8
9
11
13
5
7
5
3
3
2
1
0,3010
0,1761
0,1249
0,0969
0,0792
0,0669
0,0580
0,0512
0,0458
15,0514998
8,80456295
6,24693685
4,84550065
3,9590623
3,3473395
2,89959735
2,5576261
2,28787455
4,0514998
-4,19543705
1,24693685
-2,15449935
-1,0409377
0,3473395
-0,10040265
0,5576261
1,28787455
Chi-Quadrat =
1,09056578
1,99915568
0,24889823
0,95797479
0,27368887
0,03604198
0,00347658
0,12157636
0,72496145
5,45633972
Nun muss der berechnete Wert mit denen in der Chi-Quadrat-Tabelle verglichen
werden. Hierbei ist zu beachten, dass die Anzahl der Freiheitsgerade (FG) um einen
kleiner ist, als die Menge der verschiedenen xi:
FG=9-1=8
Wenn der Tabellenwert
 (2FG , ) kleinegleich ist als der berechnete Wert (2gemessen) ,
dann kann man mit einer Irrtumswahrscheinlichkeit α behaupten, dass den ersten
Ziffern der Länderflächen wohl eine andere Verteilung als die Benford Verteilung
zugrunde liegt.
Aus dem Blick in die Chi-Quadrat-Tabelle in der Spalte für 8 Freiheitsgerade erhält
man für α=5%:,
 (2FG , )   (2gemessen )
 (2FG ,5%)   (2gemessen )
15,5  5,5
Somit lässt sich nicht behaupten, dass sich die Verteilung der ersten Ziffer bei den
Länderflächen und die Benford Verteilung signifikant unterscheiden.