Lösungen zu Fallstudie 2.1 zur Grenzplankostenrechnung

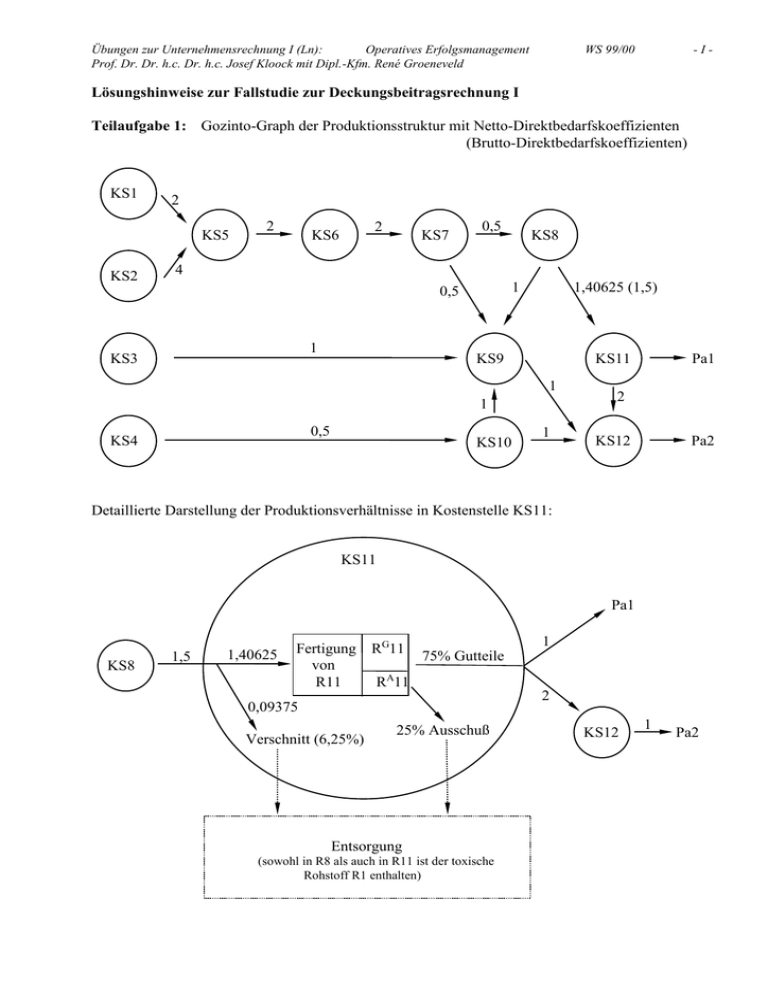
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
-I-
Lösungshinweise zur Fallstudie zur Deckungsbeitragsrechnung I
Teilaufgabe 1: Gozinto-Graph der Produktionsstruktur mit Netto-Direktbedarfskoeffizienten
(Brutto-Direktbedarfskoeffizienten)
KS1
2
KS5
KS2
2
2
KS6
KS7
0,5
KS8
4
1
0,5
1
KS3
1,40625 (1,5)
KS9
1
1
0,5
KS4
KS10
Pa1
KS11
1
2
Pa2
KS12
Detaillierte Darstellung der Produktionsverhältnisse in Kostenstelle KS11:
KS11
Pa1
KS8
1,5
1,40625
Fertigung RG11
75% Gutteile
von
R11
RA11
1
2
0,09375
Verschnitt (6,25%)
25% Ausschuß
Entsorgung
(sowohl in R8 als auch in R11 ist der toxische
Rohstoff R1 enthalten)
KS12
1
Pa2
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
- II -
Teilaufgabe 2:
Die Direktbedarfskoeffizienten können mit Ausnahme von a 8p,11 aus der Aufgabenstellung übernommen werden. Abgesehen von der Ausnahme entsprechen sämtliche Netto-Direktbedarfskoeffizienten auch den jeweiligen Brutto-Direktbedarfskoeffizienten.
Da der Verschnitt je produzierter Mengeneinheit von R11 anfällt, stellt er Einzelkosten dar und ist
durch Einführung des Brutto-Direktbedarfskoeffizienten zu erfassen.
p
a 8,11 =
1, 40625
 100 = 1,5.
(100  6 , 25)
Der Ausschuß von 25% der produzierten Mengeneinheiten stellt variable Gemeinkosten dar, da er
zwar in Abhängigkeit von der Produktionsmenge R11 anfällt, aber nicht je Mengeneinheit von R11
entsteht. Prinzipiell sind die durch die Ausschußproduktion hervorgerufenen Mehrverbräuche und
Kosten gesondert zu erfassen. Es ist jedoch möglich, die Mehrverbräuche im Gozinto-Modell der
Einzelkostenplanung zusätzlich zu erfassen und abzubilden, wobei darauf geachtet werden muß,
daß im Rahmen der Einzelkostenplanung keine Verrechnung von Ausschußkosten erfolgt.
Hierbei sind grundsätzlich folgende Möglichkeiten zur Abbildung des Ausschusses denkbar:
a) Erfassung der Ausschußproduktion mit Hilfe des Direktbedarfskoeffizienten a8,11
1
p*
p
=2
a8,11  a8,11 
0,75
- korrekte Erfassung des durch den Ausschuß hervorgerufenen Mehrverbrauchs an Rohstoffen
- keine Erfassung der durch die Ausschußproduktion hervorgerufenen Fertigungskosten der
Kostenstelle KS11
b) Erfassung der Ausschußproduktion mit Hilfe von Eigenbedarf von Kostenstelle KS11
p
b1111
1
,
p**
p
p**
Es gilt: b1111
,  b1111
,  1, 33  1  0, 33
,  (1  0,25)  0,75  1, 33 und somit b1111
Diese Differenz stellt den fiktiven Gesamteigenbedarf dar, den die Stelle KS11 für eine ME
R11 bereitzustellen hat. Dieser Gesamteigenbedarf stellt den Grenzwert einer geometrischen
Reihe dar multipliziert mit dem Startglied der geometrischen Reihe als „Primärinput“. Daher
folgt
p**
0, 33 
a1111
,
p**
1  a1111
,
p**
 a1111
,  0,25
c) Erfassung der Ausschußproduktion mit Hilfe der KS11 nachgelagerten Direktbedarfskoeffizienten
p
a11, Absatz
1
p***
a11, Absatz 

 1, 33
1  0,25
0,75
p
a1112
2
,
p***
a1112
,  1  0,25  0,75  2, 66
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
- III -
d) Erfassung der Ausschußproduktion als Kuppelproduktion in der Stelle KS11
nicht weiter behandelt
e) Erfassung durch eine gesonderte Ausschußrechnung
nicht weiter behandelt
Unabhängig davon, wie der Ausschuß modelltheoretisch abgebildet wird, ist darauf zu achten, daß
im Rahmen der Ermittlung der Material- bzw. Fertigungseinzelkosten der Absatzmengen die nicht
modifizierte Gesamtbedarfsmatrix herangezogen wird. Im Rahmen der Planung der variablen
Gemeinkosten ist dann auf eine der oben beschriebenen Varianten zurückzugreifen, wobei u.U. die
Differenz aus den durch die jeweilige Variante erhaltenen und den anhand der nicht modifizierten
Gesamtbedarfsmatrix hergeleiteten Werte gebildet werden muß, um die für die Gemeinkostenrechnung relevanten Daten zu erhalten.
Sofern der Ausschuß (entgegen seinem eigentlichen Charakter) als Einzelkosten interpretiert wird,
ist für die Einzelkostenrechnung eine der oben beschriebenen Varianten heranzuziehen (Vorsicht:
bei a) sind die für den Ausschuß anfallenden Fertigungskosten dann noch gesondert zu berücksichtigen).
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
- IV -
Teilaufgabe 3:
r p  A  r p  xa p
 r p  ( E  A ) 1  xa p
gesucht ist ( E  A ) 1 =: B
Zunächst erfolgt die Herleitung der Gesamtbedarfsmatrix zur Materialbedarfsplanung ohne
p
Berücksichtigung von Ausschuß, aber unter Berücksichtigung von Verschnitt: a 8,11 = 1,5.
1

0
0

0
0

0
(E  A) 1  
0

0

0
0

0

0
0 0 0 2 4 8
1 0 0 4 8 16
0 1 0 0 0
0 0 1 0 0
0
0
0 0 0 1 2
0 0 0 0 1
4
2
0 0 0 0 0
0 0 0 0 0
1
0
0 0 0 0 0
0 0 0 0 0
0
0
0 0 0 0 0
0 0 0 0 0
0
0
20 

40 
0
1
0
0
1

0 0,5 0,5
0
1
2
4
0
3
10 

1
2
0 1,5
5
0,5 1
0 0,75 2,5

1
1
0 1,5
4

0
1
0
0
1
0
1
1
0
2

0
0
0
1
2

0
0
0
0
1
4
8
8
16
0
0
6
12
Entweder durch Multiplikation der Gesamtbedarfsmatrix mit dem Vektor der Absatzmengen oder
durch Lösen des folgenden Gleichungssystems ergeben sich die nachstehenden Gesamtbedarfs.
g1:
g2:
g3:
g4:
g5:
g6:
g7:
g8:
g9:
g10:
g11:
g12:
r1
r2
r3
r4
r5
r6
r7
r8
r9
r10
r11
r12
=
=
=
=
=
=
=
=
=
=
=
=
2  r5
4  r5
1  r9
0,5  r10
2  r6
2  r7
0,5  r8 + 0,5  r9
1  r9 + 1,5  r11
1  r12
1  r9 + 1  r12
2  r12 + 5.000
6.000












r1
r2
r3
r4
r5
r6
r7
r8
r9
r10
r11
r12
=
=
=
=
=
=
=
=
=
=
=
=
150.000
300.000
6.000
6.000
75.000
37.500
18.750
6.000 + 1,5  17.000 = 31.500
6.000
6.000 + 6.000 = 12.000
12.000 + 5.000 = 17.000
6.000
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
-V-
Zur Berücksichtigung von Verschnitt mit ausgewählten Varianten aus Teilaufgabe 2:
zu Variante a) aus Teilaufgabe 2:
p
Zur Ermittlung der Gesamtbedarfsmatrix ist der Direktbedarfskoeffizient a8,11  1,5 durch
p*
a8,11  2 zu ersetzen. Dies führt zu
1

0
0

0
0

1  0
(E  A*)  
0

0

0
0

0

0
0 0 0 2 4 8
1 0 0 4 8 16
0 1 0 0 0
0 0 1 0 0
0
0
0 0 0 1 2
0 0 0 0 1
4
2
0 0 0 0 0
0 0 0 0 0
1
0
0 0 0 0 0
0 0 0 0 0
0
0
0 0 0 0 0
0 0 0 0 0
0
0
8 24

16 48
0
1
0 0 1

0 0,5 0,5 0 1 
2
4
0 4 12

1
2
0 2 6
0,5 1
0 1 3

1
1
0 2 5

0
1
0 0 1
0
1
1
0 2

0
0
0 1 2

0
0
0 0 1
4
8
8
16
0
0
Entweder durch Multiplikation der Gesamtbedarfsmatrix mit dem Vektor der Absatzmengen oder
durch Lösen des nachstehenden Gleichungssystems ergeben sich die nachstehenden Gesamtbedarfe.
g1:
g2:
g3:
g4:
g5:
g6:
g7:
g8:
g9:
g10:
g11:
g12:
r1* =
r2* =
r3* =
r4* =
r5* =
r6* =
r7* =
r8* =
r9* =
r10* =
r11* =
r12* =
2  r5*
4  r5*
1  r9*
0,5  r10*
2  r6*
2  r7*
0,5  r8* + 0,5  r9*
1  r9* + 2  r11*
1  r12*
1  r9* + 1  r12*
2  r12* + 5.000
6.000
 r1*
 r2*
 r3*
 r4*
 r5*
 r6*
 r7*
 r8*
 r9*
 r10*
 r11*
 r12*
=
=
=
=
=
=
=
=
=
=
=
=
184.000
368.000
6.000
6.000
2  46.000 = 92.000
2  23.000 = 46.000
0,5  (40.000 + 6.000) = 23.000
6.000 + 2  17.000 = 40.000
6.000
6.000 + 6.000 = 12.000
2  6.000 + 5.000 = 17.000
6.000
Zu beachten ist, daß durch diese Variante keine Berücksichtigung der durch den Ausschuß
hervorgerufenen Mehrbeschäftigung in KS11 erfolgt.
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
- VI -
zu Variante b) aus Teilaufgabe 2:
p
Zur Ermittlung der Gesamtbedarfsmatrix ist der Direktbedarfskoeffizient a1111
,  0,25 einzuführen.Dies führt zu
1

0
0

0
0

1  0
(E  A * *)  
0

0

0
0

0

0
0 0 0 2 4 8
1 0 0 4 8 16
0 1 0 0 0
0 0 1 0 0
0
0
0 0 0 1 2
0 0 0 0 1
4
2
0 0 0 0 0
0 0 0 0 0
1
0
0 0 0 0 0
0 0 0 0 0
0
0
0 0 0 0 0
0 0 0 0 0
0
0
24 

48 
0
1
0
0
1 

0 0,5 0,5
0
1 
2
4
0
4
12 

1
2
0
2
6 
0,5 1
0
1
3 

1
1
0
2
5 

0
1
0
0
1 
0
1
1
0
2 

0
0
0 1, 33 2, 66

0
0
0
0
1 
4
8
8
16
0
0
8
16
Entweder durch Multiplikation der Gesamtbedarfsmatrix mit dem Vektor der Absatzmengen oder
durch Lösen des nachstehenden Gleichungssystems ergeben sich die nachstehenden Gesamtbedarfe.
g1:
g2:
g3:
g4:
g5:
g6:
g7:
g8:
g9:
g10:
r1**
r2**
r3**
r4**
r5**
r6**
r7**
r8**
r9**
r10**
=2  r5**
=4  r5**
=1  r9**
=0,5  r10**
=2  r6**
=2  r7**
=0,5  r8** + 0,5  r9**
=1  r9** + 1,5  r11**
=1  r12**
=1  r9** + 1  r12**
g11: r11** =0,25 r11** + 2  r12** + 5.000
g12: r12** =6.000
 r1** =
 r2** =
 r3** =
 r4** =
 r5** =
 r6** =
 r7** =
 r8** =
 r9** =
 r10** =
184.000
368.000
6.000
6.000
2  46.000 = 92.000
2  23.000 = 46.000
0,5  (40.000 + 6.000) = 23.000
6.000 + 1,5  22.666,66 = 40.000
6.000
6.000 + 6.000 = 12.000
2  6000  5000
 22.666, 66
 r11** =
(1  0,25)
 r12** = 6.000
Durch diese Variante wird für sämtliche Kostenstellen die unter Einbeziehung von Ausschuß entstehende Gesamtbeschäftigung ermittelt.
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
- VII -
zu Variante c) aus Teilaufgabe 2:
p
Zur Ermittlung der Gesamtbedarfsmatrix sind die Direktbedarfskoeffizienten a11, Absatz  1 bzw.
p***
p
p***
a1112
,  2 durch a11, Absatz  1, 33 bzw. a1112
,  2, 66 zu ersetzen. Da in der Gesamtbedarfsmatrix
p***
keine gesonderte Absatzstelle vorhanden ist, für die a11, Absatz  1, 33 angesetzt werden kann, ist
hilfsweise die Absatzmenge von Pa1 mit diesem Faktor zu multiplizieren, was zu einem
modizifizerten Absatzmengenvektor führt. Die Gesamtbedarfsmatrix besitzt nun folgende Gestalt:
1

0
0

0
0

0
(E  A * *) 1  
0

0

0
0

0

0
0 0 0 2 4 8
1 0 0 4 8 16
4
8
8
16
0
0
8
16
0 1 0 0 0
0 0 1 0 0
0
0
0
0
1
0
0,5 0,5
0 0 0 1 2
0 0 0 0 1
4
2
2
1
4
2
0
0
4
2
0 0 0 0 0
0 0 0 0 0
1
0
0,5
1
1
1
0
0
1
2
0 0 0 0 0
0 0 0 0 0
0
0
0
0
1
1
0
1
0
0
0 0 0 0 0
0 0 0 0 0
0
0
0
0
0
0
0
0
1
0
0
0
24 

48 
1 

1 
12 

6 
3 

5 

1 
2 

2, 66

1 
Entweder durch Multiplikation der Gesamtbedarfsmatrix mit dem modifizierten Vektor der
Absatzmengen oder durch Lösen des nachstehenden Gleichungssystems ergeben sich die
nachstehenden Gesamtbedarfe.
g1:
g2:
g3:
g4:
g5:
g6:
g7:
g8:
g9:
g10:
g11:
g12:
r1*** =
r2*** =
r3*** =
r4*** =
r5*** =
r6*** =
r7*** =
r8*** =
r9*** =
r10*** =
r11*** =
r12*** =
2  r5***
4  r5***
1  r9***
0,5  r10***
2  r6***
2  r7***
0,5  r8*** + 0,5  r9***
1  r9*** + 1,5  r11***
1  r12***
1  r9*** + 1  r12***
2,66  r12*** + 1,33  5.000
6.000












r1*** =
r2*** =
r3*** =
r4*** =
r5*** =
r6*** =
r7*** =
r8*** =
r9*** =
r10*** =
r11*** =
r12*** =
184.000
368.000
6.000
6.000
2  46.000 = 92.000
2  23.000 = 46.000
0,5  (40.000 + 6.000) = 23.000
6.000 + 1,5  22.666,66 = 40.000
6.000
6.000 + 6.000 = 12.000
2, 66  6.000  1, 33  5000  22.666, 66
6.000
Durch diese Variante wird für sämtliche Kostenstellen die unter Einbeziehung von Ausschuß entstehende Gesamtbeschäftigung ermittelt.
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
- VIII -
Ermittlung der Einstandspreise:
R1
R2
R3
R4
Wiederbeschaffungspreis (WP)
1,17
1,25
2,11
1,50
Transportkosten
0,12
0,12
0,12
0,12
Gefahrenzulage
1,10
0,0625
0,1055
0,075
Versicherung (5% auf WP)
Einstandspreis pbpm
2,39
1,4325
2,3355
1,695
Teilaufgabe 4:
Optimale Bestellungen r* für die einzelnen Faktoren.
Vgl. Skript S. 115f. für die Symbolik!
K(r)  B(r)  L(r) 
RJ
RJ
r
 kbf +  klv  T
r
2
r* = 2 

kbf
klv
T
RJ kbf

T klv
r*
RJ/r*
R1
184.000
6.250
0,09
12
46.147,91  46.000
4
R2
368.000
5.865
0,17
12
46.000
8
R3
6.000
1.000
0,25
12
2.000
3
R4
6.000
1.800
0,20
12
3.000
2
Für Rohstoff R1 ist diejenige Konstellation zu wählen, die bei Bereitstellung der gewünschten
Jahresrohstoffmenge, bei Erfüllung der Ganzzahligkeitsbedingung für die Anzahl der Bestellungen
und unter Berücksichtigung der Containergröße von 1.000 kg, die minimalen Jahresbestellkosten
ermöglicht.
r=46.000 ME

K = 4*6.250 + 23.000*0,09*12 = 49.840 Euro
Für r = 47.000 ME ist offensichtlich, daß höhere Jahreskosten entstehen, da die Anzahl der Bestellungen aufgrund der Ganzzahligkeitsbedingung unverändert bleibt und zugleich die Lagerkosten
steigen.
Übungen zur Unternehmensrechnung I (Ln):
Operatives Erfolgsmanagement
Prof. Dr. Dr. h.c. Dr. h.c. Josef Kloock mit Dipl.-Kfm. René Groeneveld
WS 99/00
- IX -
Teilaufgabe 5:
Es wird im folgenden davon ausgegangen, daß der entstehende Ausschuß variable Gemeinkosten
verursacht, die erst im Rahmen der Kostenstellenrechnung Berücksichtigung finden. (Sofern eine
Erfassung der Ausschußkosten als Einzelkosten erfolgen soll, ist eine der in Teilaufgabe 2) bzw. 3)
beschriebenen Varianten der Mengenplanung heranzuziehen. Um Doppelerfassungen zu vermeiden,
ist von einer Verrechnung der Ausschußkosten im Rahmen der Kostenstellenrechnung abzusehen.)

Plan-Materialeinzelkosten je Absatzproduktart
M
MEKi =
 pb
m 1
p
m
 b pmi
(i =1,2)
mit
und
pbp = (2,39; 1,4325; 2,3355; 1,695)
b 
p
1-4
=
 6 20


12 40
0 1


0 1
 MEK1 = 31,53 Euro/ME
MEK2 = 109,13 Euro/ME
 gesamte primäre MEK
Produkt 1:
31,53  5.000 = 157.650
Produkt 2:
109,13  6.000 = 654.783
_______
_______

812.433
 Plan-Fertigungseinzelkosten je ME und je Absatzproduktart
M  PF
FEKi =
 pf
M 1
p
m
 b pmi
mit
und
pfp
= (0,6; 0; 0; 1,1; 0,8; 0; 0,9; 0)
b 
p
5-12
10 
 3


5
 1,5
 0,75 2,5


4
 1,5

0
1


2
 0
 1
2


1
 0
 FEK1 = 4,35
FEK2 = 13
Die Lizenzkosten sind Sondereinzelkosten der Fertigung (Skript S. 41).