Die n-te Wurzel – Beispiele

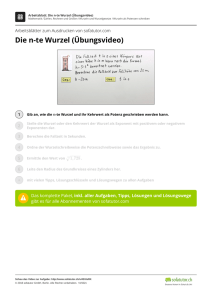
Arbeitsblatt: Die n-te Wurzel – Beispiele
Mathematik / Zahlen, Rechnen und Größen / Wurzeln und Wurzelgesetze / Wurzeln als Potenzen schreiben
Arbeitsblätter zum Ausdrucken von sofatutor.com
Die n-te Wurzel – Beispiele
1
Erkläre, wie man die n-te Wurzel als Potenz schreiben kann.
2
Gib die Wurzeln als Potenz mit positivem Exponenten an und bestimme die Lösung.
3
Berechne die Wurzel.
4
Bestimme zu jeder Potenzschreibweise die Wurzel und berechne die Lösung.
5
Leite den Wert der Potenz
6
Ermittle den Wert von 4,096 3 .
+
mit vielen Tipps, Lösungsschlüsseln und Lösungswegen zu allen Aufgaben
8
( 27
)
− 13
her.
1
Das komplette Paket, inkl. aller Aufgaben, Tipps, Lösungen und Lösungswege
gibt es für alle Abonnenten von sofatutor.com
Schau das Video zur Aufgabe: http://www.sofatutor.ch/v/43W/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V15620
1
Arbeitsblatt: Die n-te Wurzel – Beispiele
Mathematik / Zahlen, Rechnen und Größen / Wurzeln und Wurzelgesetze / Wurzeln als Potenzen schreiben
von 6
Erkläre, wie man die n-te Wurzel als Potenz schreiben kann.
Wähle die korrekten Schreibweisen aus.
A
√a = a
n
1
n
B
√a = 1
n
a
n
C
√a = a
n
E
1
n
√a
Schau das Video zur Aufgabe: http://www.sofatutor.ch/v/43W/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V15620 | E14822
1
= −a n
n
1
D
1
n
√a
1
= a− n
Arbeitsblatt: Die n-te Wurzel – Beispiele
Mathematik / Zahlen, Rechnen und Größen / Wurzeln und Wurzelgesetze / Wurzeln als Potenzen schreiben
Unsere Tipps für die Aufgaben
1
von 6
Erkläre, wie man die n-te Wurzel als Potenz schreiben kann.
1. Tipp
Es gilt a1n
= a−n .
2. Tipp
Es gilt
( a n ) = a.
1
n
Schau das Video zur Aufgabe: http://www.sofatutor.ch/v/43W/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V15620
Arbeitsblatt: Die n-te Wurzel – Beispiele
Mathematik / Zahlen, Rechnen und Größen / Wurzeln und Wurzelgesetze / Wurzeln als Potenzen schreiben
Lösungen und Lösungswege für die Aufgaben
1
von 6
Erkläre, wie man die n-te Wurzel als Potenz schreiben kann.
Lösungsschlüssel: A, D
Wurzeln können auch als Potenzen geschrieben werden:
1
n
a = a n und
√
1
1
= a− n .
n a
√
Zum Nachweis der Identität
1
n
n
a = a n beginnt man mit a = a1 = a n .
√
Nun können Regeln für das Rechnen mit Potenzen angewendet werden:
1
n
a n = a n ⋅n
= (a n ) .
n
1
Da die
n-te Wurzel die Umkehrung des Potenzierens mit n ist, gilt
n
(√
a)n = a.
Da die Werte der beiden Potenzen übereinstimmen, müssen auch die Basen übereinstimmen. Es gitl also
1
n
a = an .
√
Da a1n
1
√a
n
1
= a− n ist, kann auch
1
= a− n
abgeleitet werden.
Schau das Video zur Aufgabe: http://www.sofatutor.ch/v/43W/aRK
© 2016 sofatutor GmbH, Berlin. Alle Rechte vorbehalten. V15620