Übungsaufgaben zur 1. Klausur in 13.2

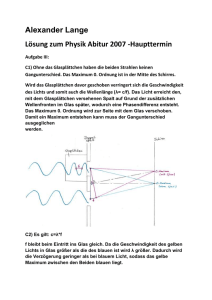
Übungsaufgaben zur 1. Klausur in 13.2
Liebe Schüler,
hier findet ihr eine Zusammenstellung von Aufgaben zur Quantenphysik, die in früheren
Klausuren gestellt wurden. Zu manchen Aufgaben habe ich kurze Musterlösungen (blau)
und Anmerkungen zu typischen Schülerfehlern (rot) erstellt.
Bitte übt auch zu Hause eine gute Darstellung, legt stets die zugrunde liegenden Gedanken
dar und erläutert die Formeln aus den Grundgesetzen!
Viel Erfolg und Durchhaltevermögen bei den Übungen!
B. Kopetschke.
Angaben:
Elektronenmasse
h = 6,6218·10-34 Js;
me = 9,105·10-31 kg
e = 1,602·10-19 C;
cLicht = 3,0 · 108 m/s
Aufgabe 1) (10 Punkte) Eine Zinkplatte ist mit einem negativ geladenen Elektroskop
verbunden.
a) Welche Beobachtungen erwarten sie, wenn man die Platte erst mit rotem Licht, dann mit UVLicht bestrahlt?
b) Erklären Sie die Beobachtungen und erläutern Sie, warum diese Beobachtungen mit der
klassischen Wellentheorie des Lichtes im Widerspruch stehen.
c) UV-Licht der Wellenlänge λ = 200 nm trifft auf eine Zinkplatte (Ablösearbeit WA = 4,2 eV).
Welche Energie haben die schnellsten abgetrennten Elektronen?
Lösungsvorschlag zu Aufgabe 1: (Verkürzt und ohne Gewähr für Richtigkeit!!)
a) Beobachtungen: rotes Licht => keine Änderung; UV-Licht: Elektroskop wird entladen.
b) Erklärung der Beobachtung: Photonen besitzen die Energie Wqu = h · f = h · c/λ .
Um eine Elektron aus der Zink-Oberfläche abzutrennen muss eine gewisse Energie, die
Ablöseenergie WA aufgebracht werden. Da rotes Licht Quanten mit großer Wellenlänge bzw.
kleiner Energie enthält, ist es zur Abtrennung nicht in der Lage. UV-Licht besitzt dagegen viel
energiereichere Quanten, die Elektronen abtrennen können. => Entladung des Elektroskops.
Widerspruch zur klassischen Theorie: Nach der klassischen Theorie wirkt auf die Elektronen im
Metall die elektrische Feldkraft, die sie aus dem Metall herauszieht. Elektronen sollten dann
abgetrennt werden, wenn die Feldstärke groß genug ist und lange genug in die gleiche Richtung
wirkt.
Eine Ablösung wäre also erst ab einer gewissen Intensität (E2) der Strahlung möglich sein. Sie
sollte um so leichter erfolgen, je niedriger die Frequenz ist.
Beides wird im Experiment nicht beobachtet, da blaues Licht auch bei sehr geringer Helligkeit
noch Elektronen abtrennen kann, und da die Abtrennung um so leichter erfolgt, je höher die
Frequenz ist.
c) Quantenenergie wird zur Ablösung benutzt, wobei im Idealfall noch Wkin übrig bleibt.
EES: Wqu = WA + Wkin =>
Wkin = QQu - WA
Wkin = h · c/λ - e · U
Wkin = 3,2 · 10-19 J = 2,0 eV
Aufgabe 2) (18 Punkte) Elektronen aus einer Glühkathode werden mit
UA = 5,0 kV beschleunigt, durchstrahlen einen sehr dünnen
polykristallinen Metallfilm und gelangen danach auf einen
Fluoreszenzschirm, welcher das abgebildete Beugungsmuster zeigt.
a) Die Stromstärke betrage 20 μA. Wie viele Elektronen durchfliegen
pro Sekunde die Apparatur, welche Energie und welche Wellenlänge
habe sie?
b) Erklären Sie qualitativ das Zustandekommen des oberen
Beugungsbildes.
c) Nun fliegen die Elektronen durch einen Doppelspalt. Auf dem 3,5
m entfernten Schirm kann man mit dem Mikroskop das unten
abgebildete Beugungsmuster sehen. Berechnen sie den Abstand der
beiden Spaltmitten.
d) Welche Masse und welche Energie müssten Photonen besitzen,
damit sie das gleiche Beugungsmuster wie in c) hervorbringen?
x in mm
0
0, 0,
1 2
Lösungsvorschlag zu Aufgabe 2) (Verkürzt und ohne Gewähr!!)
a) N sei die Zahl der pro Sekunde durchfliegenden Elektronen:
I = Q/t = N · e / t => N = I·t / e = 1,2 · 1014
Energie der Elektronen
Wkin = e · U = 5,0 keV = 8,0 · 10-16 J
deBroglie-Wellenlänge der Elektronen:
λ=h/p
Wkin = ½ m·v2 = ½ p2/m
λ = 17 pm
=>
p =
2 m·Wkin
Pro Sekunde fliegen 1,2 1014 Elektronen die Apparatur. Sie besitzen die Energie 5,0 keV
und die deBroglie-Wellenlänge λ = 17 pm.
b) In dem polykristallinen Metallfilm sind viele Kristalle so ausgerichtet, dass sie zufällig die
Bragg-Bedingung erfüllen. D.h. eintreffenden deBroglie-Wellen werden, falls sie ein
Kriställchen unter dem Glanzwinkel φn treffen, reflektiert. Die reflektierten Wellen bilden mit
dem einfallenden Strahl die Winkel 2φn und liegen alle auf Kegelmänteln, deren Schnitte mit
dem Leuchtschirm Kreise ergeben. (Vergleiche Skript!)
c) Bei Beugung am Doppelspalt gilt für die Maxima: sin α = k · λ/g (k = 0,1,2…)
Da α hier extrem klein ist, gilt weiterhin: sin a = tan α = d/a
=> dk / a = k · λ/g
=> g = k·λ·a / dk
Für k = 2 entnimmt man aus der Abbildung: d2 = 0,1 mm.
=> g = 1,2 μm
d) Damit das gleiche Beugungsmuster entsteht, müssen die Photonen die gleiche Wellenlänge
wie die Elektronen besitzen.
W = h · f = h · c/λ = 1,1·10-14 J = 7,2 keV
W = m · c2 => m = W / c2 = 1,2 ·10-31 kg.
Die Photonen müssen die Energie Wqu = 7,2 keV und die Masse m = 1,2·10-31 kg besitzen.
Aufgabe 3) (6 Punkte) a) Was besagt die Heisenbergsche Unbestimmtheitsrelation und welche
Konsequenzen hat sie für Mikroobjekte?
b) Zeigen Sie anhand eines selbst gewählten Beispiels (auch durch Rechnung), warum die
Heisenbergsche Unbestimmtheitsrelation bei makroskopischen Objekten keine Rolle spielt.
Lösungsvorschlag zu Aufgabe 3) (Verkürzt und ohne Gewähr!!)
Heisenbergsche Unbestimmtheitsrelation: Δx · Δpx  h
Δx ist hier die Unbestimmtheit der Ortsmessung, Δpx die Unbestimmtheit der x-Komponente der
Impulsmessung. Die Beziehung besagt, dass es unmöglich ist, gleichzeitig den Ort und den
Impuls eines Objektes mit beliebiger Genauigkeit zu messen. Je genauer man den Ort kennt
(kleines Δx) umso unschärfer wird der Impuls (großes Δpx). Das Produkt Δx · Δpx liegt in der
Größenordnung von h.
Konsequenz für Mikroobjekte: Wenn man bei einem Teilchen x genau kennt, weiß man nicht, in
welcher Richtung man es später finden wird. Kennt man die Richtung genau, so weiß man nichts
über seinen Ort. => Begriff Bahnkurve mach bei Mikroobjekten keinen Sinn!
(Häufig genannte falsche bzw. unzureichende Lösung: "Man kann den Ort eines Teilchens nicht
genau angeben.")
b) Beispiel: Ein Mensch (m = 100 kg, v = 1 m/s => p = 100 kgm/s) geht durch eine Türe (l = 1
m) und wird als Quantenobjekt gebeugt.
Angenommen die Querkomponente seines Impulses kenne man auf 1/1000 kgm/s genau.
Dann wäre seine Ortsunschärfe Δx  Δpx/h = 1,5·10-30 m.
D. h. auch bei extrem genauer Impulskenntnis ist die Ortsunschärfe bei Makroobjekten noch
wesentlich kleiner als der Durchmesser eines Atomkernes, so dass man von der Heisenbergscher
UBR bei Makroobjekten nichts bemerkt.
Aufgabe 4) ( Punkte)
a) Skizzieren Sie den Aufbau einer Vakuum-Fotozelle.
b) In der Tabelle sind die Fotospannungen angebeben, die sich bei Beleuchtung mit
unterschiedlichen Wellenlängen einstellen. Erklären Sie warum diese Spannungen entstehen und
wie man sie misst.
Farbe
UV
violett
blau
gelb
λ in nm
366
405
436
579
U in V
1,35
1,02
0,81
0,12
c) Zeichnen Sie das f-U-Diagramm und berechnen sie damit das Plancksche Wirkungsquantum.
d) Ermitteln Sie die Grenzfrequenz f0 und berechnen Sie daraus die Ablöseenergie des
Kathodenmaterials.
Ohne Lösungsvorschlag!  Heft!
Aufgabe 5) (10 Punkte)
a) Welche Masse und welche Wellenlänge haben Photonen der Energie 1,10 MeV? Wie nennt
man diese Sorte elektromagnetischer Strahlung?
b) Diese Photonen sind im Beisein von Materie zu Paarbildung fähig. Erkläre, was bei der
Paarbildung geschieht und berechne die Bewegungsenergie der entstehenden Teilchen.
Ohne Lösungsvorschlag!  Heft!
Aufgabe 6)(8 Punkte) Ein Laserstrahl durchläuft das
skizzierte Mach-Zehnder-Inerferometer.
a) Skizzieren Sie das am Schirm zu erwartende
Beugungsbild, wenn der Weg A exakt gleich lang ist,
wie der Weg B.
b) Was macht ein einzelnes Photon, wenn es in der
skizzierten Anordnung zum halbdurchlässigen Spiegel
HS1 gelangt?
c) Erläutern Sie an der (evtl. geringfügig erweiterten) Anordnung die Begriffe "Wahrscheinlichkeitsprinzip",
"Nichtobjektivierbarkeit" und "Superpositionsprinzip"
A
Schirm
A
B
B
HS1
Lösungsvorschlag zu Aufgabe 6) (Verkürzt und ohne Gewähr!!)
a) Wenn der Weg A genau so lang ist, wie der Weg B,
besteht nirgendwo ein Gangunterschied zwischen den beiden
Teilwellen. => Am Schirm erscheint bei nicht aufgeweitetem
Laser ein Heller Punkt oder bei aufgeweitetem Laser helle
Fläche.
Manchmal wird von Schülern der Zustand δ = k · λ ; (k = 1,2,3…) skizziert. (rechtes Bild) In diesem
Fall würden bei aufgeweitetem Laser konzentrische helle und dunkle Ringe erscheinen, wobei das
Zentrum hell wäre. Allerdings ist dann die Vorgabe "Gleich lange Wege" in der Aufgabe nicht erfüllt!
b) Da die beiden Wege ununterscheidbar sind, teilt sich die Ψ-Welle in zwei Komponenten. Ein
Teil der Welle geht über Weg A, ein anderer über Weg B. Am Schirm kommt es zur Interferenz.
c) Wahrscheinlichkeitsprinzip: |Ψ|2 gibt die Wahrscheinlichkeit an, ein Quant an einem
bestimmten Ort (z. B. auf dem Schirm) zu treffen. Ein z.B. in Weg A eingebauter Detektor
würde 50 % aller einfallenden Photonen nachweisen.
Nichtobjektivierbarkeit: Bei gleichberechtigten Wegen (wie in a) ist es unmöglich objektiv
festzustellen, ob das Quant Weg A oder Weg B gewählt hat. Es ging beide Wege!
Superpositionsprinzip: Die Ψ-Welle spaltet sich in zwei Teilwellen A und B auf, die miteinander
interferieren, d.h. ihre Wellenfunktionen überlagern sich. |Ψ|2 der resultierenden Gesamtwelle ist
ein Maß für die Antreffwahrscheinlichkeit auf dem Schirm.