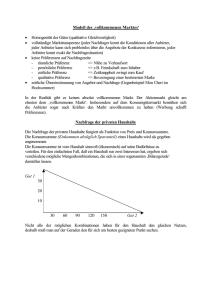
Entscheidungen in empirisch realistischer Sicht

In komplexen Entscheidungen ist der Mensch mit seinem sogenannten gesunden
Menschenverstand oft überfordert. Dies kann an der Unsicherheit der Zukunft oder an der Vielfalt
der Ziele liegen, die man anstrebt und die sich nicht voll vereinbaren lassen. Zu wenig oder zu
viele Handlungsalternativen und eine große Zahl von Einflussfaktoren können das Problem weiter
erschweren.
Durch rationales Vorgehen lassen sich die Erfolgsaussichten von Entscheidungen verbessern.
Rationalität ist kein klarer Begriff. Man kann ihn jedoch darauf konkretisieren, dass man einerseits
gewisse Anforderungen an den Entscheidungsprozess aufstellt (prozedurale Rationalität) und sich
andererseits auf Grundsätze der Konsistenz, d.h. Widerspruchsfreiheit festlegt.
Komplexe Probleme werden durch Dekomposition, d.h. Zerlegung in Teilprobleme vereinfacht.
Es gibt keine objektiv richtigen Entscheidungen. Vielmehr beruhen Entscheidungen notwendig auf
subjektiven Erwartungen, dir nur in Grenzen überprüfbar sind, sowie auf ebenfalls subjektiven
Zielen und Präferenzen des Entscheiders.
Menschen haben Mühe, ihre subjektiven Erwartungen und Präferenzen eindeutig zu artikulieren.
Entscheidungsunterstützung durch formale Verfahren muss die Unschärfe der Informationen in
Betracht ziehen, indem sie die Konsistenz der Aussagen überprüft und notfalls mit unvollständigen
Informationen auszukommen versucht.
Die deskriptive Entscheidungstheorie, die tatsächliches menschliches Entscheidungsverhalten
beschreiben und erklären will, ist von großer Bedeutung für eine entscheidungsunterstützende
Theorie.
Die präskriptive Entscheidungstheorie ist relevant für Entscheidungen auf verschiedene Gebieten.
Sie ist nicht nur für wirtschaftliche, sondern ebenso für politische, medizinische, juristische oder
technische Entscheidungen von Bedeutung. Sie soll Menschen bei komplizierten Entscheidungen
unterstützen. Ausgangspunkt ist die Tatsache, dass der Mensch Schwierigkeiten mit neuartigen,
nicht routinisierten Entscheidungssituationen hat.
Was macht Entscheidungen schwierig?
 Die Unsicherheit der Zukunft (die Auswirkungen sind nicht vorhersehbar z.B. bei
Produkteinführungen)
 Die Konsequenzen unterschiedlicher Handlungen können sich in mehr als einer Dimension
unterscheiden. (es gibt mehrere Ziele und jede Alternative hat Vorteile gegenüber der
anderen, z.B. bei Personalentscheidungen sind viele Eigenschaften der Bewerber von
Bedeutung)
 Es gibt zuwenig/zu viele Alternativen (Aufwand bis man die richtige gefunden hat)
Je mehr unsichere Einflüsse auf das Ergebnis einwirken und je mehr Ziele zu beachten sind, desto
komplexer wird die Situation. Viele politischen Entscheidungen sind von hoher Komplexität. Die
Denkweise, die die präskriptive Entscheidungstheorie vermittelt, kann in jeder
Entscheidungssituation von Nutzen sein. Diese Theorie sollte daher zum Pflichtprogramm der
Ausbildung für jene Berufe werden, die mit Entscheidungen zu tun haben.
Die präskriptive Entscheidungstheorie will Entscheidern helfen, möglichst rationale
Entscheidungen zu treffen. Man kann jedoch schlecht feststellen, ob eine Entscheidung gut oder
schlecht war. Man kann auch nicht von „rational“ oder „irrational“ sprechen, sondern eher von
„mehr oder weniger rational“. Auch ist zwischen einer rationalen und einer erfolgreichen
Entscheidung zu unterscheiden. Eine nachträgliche Erfolgskontrolle kann z.b. Schwächen des
Entscheidungsprozesses aufdecken. Die Chance für eine Ex-post-Kontrolle besteht aber nur, wenn
die Grundlagen der Entscheidung transparent dokumentiert sind. Größtmögliche Transparenz der
Entscheidungsgrundlagen herzustellen ist ein wesentliches Ziel der präskriptiven
Entscheidungstheorie, denn auf diese Weise wird auch dem sog. Hindsight-Bias entgegengewirkt.
Das ist die Neigung des Menschen, hinterher, wenn er schlauer ist, zu glauben, er sei auch vorher
schon so schlau gewesen bzw. so schlau hätte man sein müssen.
Grundprinzipien der präskriptiven Entscheidungstheorie:
Was bedeutet rational? Es handelt sich nicht um eine objektive, beweisbare Eigenschaft. Das
Streben nach Rationalität ist keine Garantie für den Erfolg einer Entscheidung. Es trägt vermutlich
dazu bei, dass Entscheidungen im Durchschnitt erfolgreicher werden, beweist dies aber nicht. Wir
unterscheiden 2 Kriterien für rationale Entscheidungsprozesse:
Das erste ist die prozedurale Rationalität und das zweite die Konsistenz.
Prozedurale Rationalität
Die Prozedur, die zur Entscheidung führt kann mehr oder weniger rational sein. Hier folgen einige
Anforderungen an Entscheidungsprozeduren:
 Der Entscheider sollte sich überlegen, ob er das richtige Problem löst. Es kann sinnvoll
sein, das ursprüngliche Problem in Teilprobleme aufzuspalten.
 Der Entscheider sollte in die Informationsbeschaffung und –verarbeitung soviel Aufwand
investieren, wie der Bedeutung der Entscheidung angemessen ist. Rationalität verlangt eine
angemessen, sorgfältige und systematische, aber nicht maximale
Entscheidungsvorbereitung
 Er sollte bei der Bildung von Erwartungen (Unsicherheit der Zukunft wird durch
Wahrscheinlichkeiten abgebildet) über die Zukunft relevante objektive Daten in Betracht
ziehen. Er sollte sich der Gefahr von Wahrnehmungsverzerrungen bewusst sein und diese
möglichst vermeiden.
 Er sollte sich über seine eigenen Ziele und Präferenzen gründlich klar werden und die
Gefahren, die aus Selbsttäuschung entstehen, vermeiden.
Konsistenz der Entscheidungsgrundlagen
Rationalität bedeutet Übereinstimmung mit gewissen Anforderungen, deren Berechtigung der
Entscheider anerkennt und nach denen er sich richten möchte. Solche „Rationalitätspostulate“
betreffen einerseits den Umgang mit Wahrscheinlichkeiten, andererseits die Bildung von
Präferenzen. Die wichtigsten Forderungen, die man gemeinhin an rationale Präferenzen stellt sind:
 Zukunftsorientierung (die Wahl zwischen Alternativen sollte nur von ihren Konsequenzen
abhängen)
 Transitivität (Wenn der Entscheider a gegenüber b vorzieht, b gegenüber c vorzieht, dann
sollte er auch a gegenüber c vorziehen)
 Invarianz (Die Präferenzen sollten nicht davon abhängen, wie das Entscheidungsproblem
dargestellt wird)
 Unabhängigkeit von irrelevanten Alternativen (ob der Entscheider a gegenüber b vorzieht
sollte unabhängig davon sein ob es eine Alternative c gibt)
Dekomposition
Die Komplexität lässt sich reduzieren, indem man das Entscheidungsproblem in Komponenten
zerlegt, deren jede einzelne und für sich modelliert wird. Die Komponenten sind:
 Die Handlungsalternative, zwischen denen zu wählen ist
 Die mit dem Ergebnis verknüpften Ziele und Präferenzen des Entscheiders,
 die Erwartungen über die Umwelteinflüsse
 die kombinierte Wirkung von Handlungsalternativen und Umwelteinflüssen auf das
Ergebnis, d.h. die Konsequenzen der Entscheidung
Subjektivität
Erwartungen und Entscheidungen sind grundsätzlich subjektiv. 2 Personen können zu
unterschiedlichen Entscheidungen kommen, ohne dass jedoch der eine rationaler handelt als
der andere. Das gründliche Überlegen der eigenen Ziele und Präferenzen kann sehr hohe
Anforderungen an die Vorstellungskraft stellen, insbesondere, wenn es um Entscheidungen
geht, deren Auswirkungen sich über viele Jahre erstrecken. Ein wesentlicher Effekt der
Beschäftigung mit der Entscheidungstheorie ist, dass sie dazu verhilft, im Laufe der Zeit
Entscheidungen bewusster von dein eigenen Erwartungen und Zielen leiten zu lassen.
Unvollständiges Wissen und das Dominanzkonzept
Wir können unsere Erwartungen über unsichere Ereignisse oft nur ungenau formulieren.
Wenn es möglich ist, eine Alternative a gegenüber einer anderen Alternative b überlegen zu
identifizieren, obwohl über die Erwartungen und/oder die Präferenzen des Entscheiders keine
vollständige Information vorliegt, spricht man von Dominanz (a dominiert b). Es gibt mehrere
Spielarten der Dominanz, diese unterscheiden sich darin, welche Informationen unvollständig
sind und welche Entscheidungsregel die Rangfolge der Alternativen bestimmen sollen.
Gibt es unter ihren Alternativen ein Projekt x, das bei jedem Zustand einen höheren Gewinn
verspricht als ein Projekt y, so ist trotz fehlender Wahrscheinlichkeitsinformation klar, dass x
einen höheren Gewinnerwartungswert aufweist als y und also dominant ist. Diese Art von
Dominanz wird als Zustandsdominanz bezeichnet.
Eine Alternative a dominiert bei Unsicherheit eine Alternative b, wenn die schlechtmögliche
Konsequenz von a immer noch besser ist als die bestmögliche Konsequenz von b. Diese
Dominanz heißt absolute Dominanz.
Anwendung und Praxisrelevanz der präskriptiven Entscheidungstheorie
Die moderne präskriptive Entscheidungstheorie ist überwiegend von US-amerikanischen
Forschern und Beratern entwickelt worden. Die Anwendungen sind vor allem in den
Bereichen, Energiewirtschaft, Sachgüterproduktion und Dienstleistungen, Medizinische
Anwendungen, Öffentliche Politik und Sonstiges untergliedert. Über die tatsächliche
Verbreitung ist es jedoch schwierig etwas zu sagen, da viele Anwendungen von Beratern und
Beratungsfirmen durchgeführt werden, oft nur 1-2 Tage dauern, oder nur in
bereichsspezifischen Zeitschriften veröffentlicht werden. Trotzdem ist das Potential dieser
Theorie in der Praxis noch lange nicht ausgeschöpft. Zum einen ist dies auf mangelnde
Kenntnisse zurückzuführen und zum anderen ist mit Akzeptanzbarrieren zu rechnen. Die
Entscheidungshilfen setzen voraus, dass der Entscheider seine wirklichen Erwartungen und
seine wahren Präferenzen rückhaltlos offen legt. Das ist nicht immer im Interesse von
Managern und Politikern, denn Offenheit gegenüber Dritten reduziert die taktischen
Möglichkeiten und ruft unter Umständen Opposition hervor.
In den publizierten Fallstudien über die Anwendungen der präskriptiven Entscheidungstheorie
spielt der Decision Analyst eine große Rolle. Dies ist meist ein externer Berater, der das
entscheidungstheoretische Instrumentarium beherrscht und einem Projektteam Rat und Hilfe
im Prozess der Problemstrukturierung und Lösung bietet. Er bringt auch das Methodenwissen
ein (nicht das Problemwissen) und ist unparteiisch und daher sehr für eine moderierende Rolle
geeignet. Einen externen Berater anzuheuern, ist jedoch nur für relativ große Entscheidungen
sinnvoll.
Zum Begriff Entscheidung und den möglichen Betrachtungsweisen der Entscheidung
Als Entscheidung wird die Wahl einer Handlungsalternative aus mehreren möglichen
Handlungsalternativen bezeichnet. Entscheiden kann folglich nur derjenige, dem verschiedene
Handlungsmöglichkeiten offen stehen.
Entscheidungen in normativer Sicht
Grundlage ist eine Anforderung oder Norm: Entscheidungen sollen rational gefällt werden. Und
rational erscheint eine Entscheidung genau dann, wenn die Handlungsalternative gewählt wird, die
unter den gegebenen Bedingungen zur größten Zielerreichung führt.
Bei Einnahme des praktisch normativen Standpunkts darf der Entscheidungsträger die für seine
Entscheidungen maßgeblichen Ziele selbst subjektiv festlegen. Dagegen beim bekennend
normativen Standpunkt werden dem Entscheidungsträger die Ziele vorgegeben.
Entscheidungen in empirisch realistischer Sicht
Aus empirisch realistischer oder deskriptiver Sicht werden Aussagen darüber gesucht, wie
Entscheidungen in der Realität tatsächlich getroffen werden. Es spielt dabei keine Rolle, ob
Entscheidungsträger rational handeln oder ob sie vielleicht ohne klare Zielvorstellungen eher
emotional entscheiden; wichtig allein ist, was sie wirklich tun. Ziel ist es, beschreiben und erklären
zu können ,wie Menschen Entscheidungsprobleme allein oder in einer Organisation lösen, wie sie
beispielsweise Entscheidungsprobleme wahrnehmen, wie sie Ziele bilden und welche Beziehungen
zwischen Zielen und zu beurteilenden Handlungsalternativen bestehen oder wie und wann die für
die Entscheidung benötigten Informationen beschafft, verarbeitet und gegebenenfalls in der
Gruppe weitergegeben werden. Die gesuchten Aussagen müssen dabei geeignet sein, anhand der
Realität überprüft und gegebenenfalls falsifiziert zu werden. Nur dann sagen sie etwas über die
Realität aus.
Einfaches Modell des Entscheidungsverhalten: Angesichts der Fülle, der auf ihn einwirkenden
Stimuli kann der Mensch nicht alle wahrnehmen; er „filtert“ mehr oder weniger bewusst nur die
heraus, auf die er vorbereitet ist und die ihm wichtig erscheinen. Nicht jeder wahrgenommene
Stimulus muss zudem zu einem Konflikt führen, in dem der Mensch nicht genau weiß, wie er
reagieren soll. Vielfach führt er sich nicht zu einer Reaktion herausgefordert oder er kennt
„Standardlösungen“ für das Problem. Dann wird er suchen. Die Suche kann sich, abhängig von der
Art des Konfliktes, nach außen (Umwelt) oder nach innen (Gedächtnis) richten. Die für einen
Konflikt gefundene Lösung kann andersartige Konflikte auslösen. Wenn seine Ergebnisse
ausreichend sicher erscheinen, wir der Entscheidungsträger sich zur Durchsetzung dieser
Alternative entschließen und dabei auf die Umwelt einwirken. Sein Entschluss stürzt ihn zugleich
zu einem neuen Konflikt, die kognitive Dissonanz. Wird die Konsonanz erreicht so ist der Mensch
mit seinem Entschluss zufrieden. Gelingt es jedoch nicht und sprechen die Informationen gegen
seine gewählte Alternative, wird der Entschluss in Frage gestellt und der ursprüngliche Konflikt
lebt wieder auf.
Verhältnis von praktisch normativer und empirisch realistischer Betrachtung der
Entscheidung
Beide Betrachtungsweisen sind grundverschiedenen, dennoch ergänzen sie sich, wenn es um einen
Beitrag zur Verbesserung von praktischen Entscheidungen geht.
Empirisch realistische Aussagen allein sind für diesen Zweck ungeeignet. Sie können bestenfalls
Gesetzmäßigkeiten weidergeben, nach denen Entscheidungen in der Realität ablaufen. Auch auf
der Grundlage von praktisch normativen Aussagen können alleine praktische Entscheidungen nicht
verbessert werden. Die Problemstellungen und Ziele, für die rationale Entscheidungen abgeleitet
werden, lassen sich nämlich aus solchen Aussagen nicht herleiten; sie müssen vorgegeben werden.
Die beiden Betrachtungsweisen ergänzen einander insoweit, als die empirisch realistische Sicht zu
realitätskonformen Zielen und Problemstellungen sowie zu den Grenzen führen kann, innerhalb
derer ein Mensch tatsächlich frei zu entscheiden vermag. Diese Ziele, Problemstellungen und
Freiräume können dann den Rahmen abstecken, der auf Basis praktisch normativer Aussagen mit
rationalen Entscheidungen ausgefüllt wird.
Betriebswirtschafslehre und Lehre von der Entscheidung
Die moderne Bwl wird heute überwiegend als entscheidungsorientierend bezeichnet. Darin kommt
die enge Beziehung zwischen der Bwl und der Lehre von der Entscheidung zum Ausdruck. Die
Lehre von der Entscheidung ist in ihrem Geltungsbereich weiter (über Entscheidungen kann
nämlich allgemein und ohne Bezug auf ökonomische Probleme nachgedacht werden).
Grundmodell der praktisch normativen Lehre von der Entscheidung
Dieses Modell verbindet zwei verschiedene Arten von Informationen:
 grundsätzlich wertfreie Aussagen über das, was der Entscheidungsträger tun kann und
welche Konsequenzen daraus jeweils zu erwarten sind (Entscheidungsfeldinformationen)
 grundsätzlich wertende Aussagen, wie der Entscheidungsträger Konsequenzen von
Entscheidungen subjektiv beurteilt, inwieweit sie ihm also erstrebenswert oder schädlich
erscheinen (Zielinformation)  siehe Seite 7
Das Entscheidungsfeld beinhaltet:
1. Aktionsraum
2. Menge möglicher Umweltzustände: Umwelt
3. Ergebnisfunktion
1. der Aktionsraum bezeichnet den Teil des Entscheidungsfeldes, der dem Einfluss des
Entscheidungsträgers unterliegt. Er umfasst alle im Rahmen des jeweiligen
Entscheidungsproblems in Betracht gezogenen Handlungsmöglichkeiten (Aktionen) des
Entscheidungsträgers. Wählbar sind somit nur Aktionen, die im Aktionsraum enthalten sind.
Auch die Aktion „nichts zu tun“, also alles einfach laufen zu lassen, kann gewählt werden, sie
muss dann aber als so genannte „Unterlassungsalternative“ explizit in den Aktionsraum
einbezogen werden. Aktionen schließen auch untereinander aus, d.h. der Entscheidungsträger
darf also im Rahmen eines Entscheidungsproblems nur eine Aktion wählen können.
2. Unter der Bezeichnung „Umwelt“ werden die als relevant angesehen Größen erfasst
 die Einfluss auf die Ergebnisse von Aktionen des Entscheidungsträgers nehmen und
 die nicht vom Entscheidungsträger festgelegt werden können.
Wie Aktionen müssen auch Umweltzustände so formuliert werden, dass sie sich gegenseitig
ausschließen. Sofern also die Umwelt über mehrere „Umweltparameter“ verfügt, haben
Umweltzustände alle diese Parameter in jeweils einer bestimmten Ausprägung zu umfassen.
3. Die Ergebnisfunktion ordnet jeder Kombination von Aktion und Umweltzustand jeweils das
Ergebnis zu (gegebenenfalls auch mehrere Ergebnisse), dem der Entscheidungsträger einen Wert
beimisst, das er also erstrebenswert findet oder zu vermeiden betrachtet. Knüpft dagegen die
Wertordnung des Entscheidungsträgers an verschiedene Ergebnisarten an und werden diese
Ergebnisse auch zu verschiedenen Zeitpunkten gewünscht, besitzt die Ergebnisfunktion den
Charakter einer Vektorfunktion. Sie ordnet dann jeder Kombination von Aktion und
Umweltzustand einen Vektor von Ergebnissen oder sogar eine Matrix von Ergebnissen zu.
Ergebnismatrix
Die Ergebnismatrix gibt einen Überblick über die für die Entscheidung relevanten Komponenten
des Entscheidungsfeldes. In der Vorspalte stehen die Aktionen, in der Kopfzeile die
Umweltzustände und in der eigentlichen Matrix erscheinen dann die den möglichen
Kombinationen aus Aktion und Umweltzustand zugeordneten Ergebnisse.
Zielplan
Zum Zielplan gehören die Präferenzen und die Ergebnisdefinition. Der Entscheidungsträger muss
sich klar darüber werden, welche Ergebnisse er mit welcher Intensität wünschenswert findet,
welche er vermeiden möchte und welche ihm gleichgültig sind. Die operationale Formulierung
diese Wertvorstellung nennen wir Zielplan.
Mit Hilfe der Ergebnisdefinitionen hebt der Entscheidungsträger aus der Fülle denkbarer
Ergebnisse diejenigen hervor, die von seiner Wertordnung erfasst werden, die er also anstrebt oder
vermeiden möchte. Dabei kann man unterscheiden zwischen:
 Artenmerkmal (Entscheidungsträger legt fest welche Art von Ergebnissen ihn interessieren)
 Höhenmerkmal
 Zeitmerkmal (Er legt fest, wann ein Ergebnis eintreten muss, damit es von seiner
subjektiven Wertordnung erfasst wird. Es kann ein Zeitpunkt oder ein Zeitintervall
angegeben werden)
 Sicherheitsmerkmal (Erfassung der Eintrittswahrscheinlichkeit des jeweiligen Ergebnisses)
In den Präferenzen drückt der Entscheidungsträger die relative Intensität aus, mit der er die
Ergebnisse anstrebt oder vermeidet. Die Präferenzen geben auch an, wie sich bei einer Variation
von Ergebnismerkmalen die Einstellung des Entscheidungsträgers dieses Ergebnisses gegenüber
verändert. Im einfachen Fall beschreiben Präferenzen Wertverhältnisse, die sich aus der
Veränderung nur eines Ergebnismerkmals bei Konstanz aller übrigen Merkmale ergeben. Es gibt
noch ordinale Präferenzen (geben nur die Ordnung an) und kardinale Präferenzen (beinhalten
darüber hinaus Aussagen über die Größe der Nutzenunterschiede beim Vergleich mehrerer
Ergebnisse). Es kann wieder zwischen folgenden Präferenzen unterschieden werden:
 Subjektive Artenpräferenz (drückt die relative Vorteilhaftigkeit nur aufgrund der
Artenmerkmale aus; Beispiel: „Gewinn ist vorteilhafter als Umsatz“ = ordinale
Artenpräferenz; „Gewinn ist fünfmal so vorteilhaft wie Umsatz“ = kardinale
Artenpräferenz)



Subjektive Höhenpräferenz (Höhenmerkmale sind ausschlaggebend; Beispiel: „je höher
desto besser“ = ordinal; „die Vorteilhaftigkeit gleicher Ergebnisse sind proportional zu
ihren Ergebnishöhen“ = kardinal)
Subjektive Zeitpräferenz (unterschiedlicher zeitlicher Eintritt ist von Vorteil; Beispiel: „je
früher desto besser“ = ordinal; „ein um eine Periode früher anfallendes Ergebnis ist 1,1-mal
so viel wert wie ein anderes“ = kardinal)
Subjektive Sicherheitspräferenz („je größer die Wahrscheinlichkeit des Eintritts, desto
besser“ = ordinal; „Vorteilhaftigkeit von gleichen Ergebnissen ist proportional zu den
Wahrscheinlichkeiten ihres Eintritts = kardinal)
Entscheidungsmatrix
In den Entscheidungsmatrizen werden die Informationen über das Entscheidungsfeld mit den in der
Ergebnismatrix noch nicht erfassten Zielplaninformationen, also den Präferenzen, verbunden. Erst
die Entscheidungsmatrix weist einen Gesamtnutzen aus. Charakteristisch für diese
Entscheidungsmatrix ist also, dass sie für jede Aktion nur noch eine Größe, den Gesamtnutzen,
ausweist, dass sie also zu einem Spaltenvektor degeneriert ist. Genau diese Vereinfachung wurde
mit der Verschmelzung von Präferenzen und Ergebnismatrix zur Entscheidungsmatrix angestrebt.
Im Aktionsraum können als Aktionen auch Folgen von Teilentscheidungen des
Entscheidungsträgers zu verschiedenen künftigen Zeitpunkten erfasst werden. Um Folgen von
Teilentscheidungen von „einfachen“ Aktionen zu unterscheiden, werden sie häufig Strategien
genannt. Um mehrstufige Entscheidungen übersichtlicher darstellen zu können, verwendet man
den Entscheidungsbaum. Dieser zeigt den Ablauf von Teilentscheidungen und Umweltzuständen.
Entscheidungen bei Sicherheit
Entscheidungen bei Sicherheit zeichnen sich dadurch aus, dass die Umwelt nur einen vorab
bekannten Zustand annehmen kann. Bei Entscheidungen einer Ergebnisart und Ergebnissen in
mehreren Zeitpunkten spricht man häufig von Investitionen, Investitionsrechnung oder- theorie.
Dem wird in der Bwl hohe Aufmerksamkeit geschenkt. Schwierigkeiten dabei bereitet oft das
Einbeziehen von Zins.
Entscheidungen bei Unsicherheit
Entscheidungsmodelle, in denen keine Sicherheit herrscht, zeichnen sich dadurch aus, dass die
Umwelt einen von mehreren in Betracht gezogenen Zuständen annehmen kann. Es bedeutet, dass
nicht sicher ist, welcher von mehreren möglichen, aber bekannten Umweltzuständen eintritt. Im
Falle des Risikos besitzt der Entscheidungsträger Vorstellungen über die
Eintrittswahrscheinlichkeiten der verschiedenen Umweltzustände. Diese Wahrscheinlichkeiten
genügen stets den drei Axiomen:
 Nichtnegativität (Wahrscheinlichkeiten sind nie negativ)
 Normierung (die Wahrscheinlichkeit des sicheren Ereignisses ist 1, die eines unmöglichen
Ereignisses ist 0)
 Additivität (die Wahrscheinlichkeit dafür, dass das eine oder das andere von zwei sich
gegenseitigen ausschließenden Ereignissen eintritt, entspricht der Summe der
Eintrittswahrscheinlichkeiten dieser Ereignisse).
Die Wahrscheinlichkeiten müssen jedoch nicht objektiv sein, es genügen auch subjektive (= von
persönlichen Gefühlen/Interessen/Vorurteilen bestimmt) Wahrscheinlichkeiten.
In einer Spielsituation entscheidet ein rationaler „Gegenspieler“ des Entscheidungsträgers darüber,
welcher Umweltzustand eintritt und er verfolgt dabei seine eigenen Ziele. Es gibt das
Konstantsummen-Spiel (die Summen der Ergebnishöhen des Spielers und des Gegenspieles sind
gleich groß) oder das Nullsummen-Spiel (Gewinn des einen ist gleich der Verlust des anderen)
Entscheidungen bei Unsicherheit
Bei Unsicherheit kennt der Entscheidungsträger, was die Umwelt betrifft, nur die möglichen
Zustände. Er weiß jedoch nicht mit welcher Wahrscheinlichkeit diese Zustände eintreten. Für die
Unsicherheit sind in der Literatur mehrere so genannte „Entscheidungsregeln“ entwickelt worden.
Sie implizieren außer einer besonderen Sicherheitspräferenz auch noch die Höhenpräferenz.
Dabei gibt es folgende Methoden:
Minimax-Regel:
Ergibt nur Sinn, wenn sie auf eine Ergebnismatrix angewendet wird und wenn dem
Entscheidungsträger die negative Höhenpräferenz (je niedriger desto besser) wichtig ist. Er wählt
die Aktion mit dem minimalen Schadensmaximum. Ich nehme von den schlechtmöglichsten
Varianten die bestmögliche. Diese Regel beschreibt die Sicherheitspräferenz eines extremen
Pessimisten.
Maximax-Regel:
Aus den besten Alternativen wird noch einmal die beste ausgewählt. Die beschreibt die
Sicherheitspräferenz eines extremen Optimisten.
Pessimismus-Optimismus-Regel: (Hurwicz)
Diese Regel erlaubt Kompromisse aus den beiden zuvor behandelten Entscheidungsregeln. Sie
fasst das größtmögliche Ergebnis jeder Aktion, gewichtet mit dem Faktor λ, und das niedrigste
Ergebnis jeder Aktion, gewichtet mit dem Faktor 1- λ, zu einem Vorteilhaftigkeitsmaß zusammen.
Im Faktor λ drückt der Entscheidungsträger seine persönliche Einstellung zur Unsicherheit aus.
Das Maximum aus den ausgerechneten Ergebnissen ist die Lösung.
Laplace-Regel:
Da die Eintrittswahrscheinlichkeit unbekannt ist, wird unterstellt, dass alle Umweltzustände gleich
wahrscheinlich sind. Optimal ist die Aktion mit der größten Summe. Bei 4 Varianten ist die
Wahrscheinlichkeit 0,25, bei 2 ist sie 0,5.
Minimax-Risiko-Regel: (Savage-Niehans-Regel)
Als optimal wir die Aktion bezeichnet, deren größtmöglicher Nachteil verglichen mit den
größtmöglichen Nachteilen der übrigen Aktionen am niedrigsten ist. Ich welche die besten
Alternativen aus und daraus dann das Minimum.
Entscheidung bei Risiko
Ähnlich wie bei der Situation der Unsicherheit werden auch hier einige Entscheidungsprinzipien
angeboten, wobei mit jedem dieser Prinzipien spezifische Sicherheits- und Höhenpräferenzen zum
Ausdruck gebracht werden.
Erwartungswert-Prinzip:
In der Risikosituation liegt es nahe, die Ergebnishöhen der möglichen Ergebnisse einer Aktion mit
deren Eintrittswahrscheinlichkeit zu gewichten und aufzusummieren. Die sich daraus ergebenden
Erwartungswerte von Wahrscheinlichkeitsverteilungen über Ergebnishöhen sind die
Vorteilhaftigkeitsmaße, die beim Erwartungswert-Prinzip (μ-Prinzip) aufgegriffen werden. Es
passt weder zu einem risikofreudigen, noch zu einem risikoscheuen Mensch.
(μ, δ)-Prinzip:
Bei diesem Prinzip werden die in der Risikosituation mit Aktionen verbundene
Wahrscheinlichkeitsverteilungen von Ergebnissen nicht nur anhand ihres Erwartungswertes μ,
sonder auch anhand ihrer Standardabweichung δ beurteilt. Dabei stellt die Standardabweichung ein
in der Statistik verbreitetes Maß für die Streuung einer Wahrscheinlichkeitsverteilung dar. Im
Gegensatz zum Erwartungswertprinzip kann dieses Prinzip Risikofreude durch ein positives
Gewicht für δ und Risikoscheu durch ein negatives Gewicht für δ widerspiegeln.
Bernoulli-Prinzip:
Mit Hilfe geeigneter Bernoulli-Nutzenfunktionen lassen sich verschiedene Einstellungen
ausdrücken, die in der Literatur als Risikoneutralität, Risikofreude und Risikoscheu bezeichnet
werden. Die Funktion u(e) = √e.
Risikoneutralität = Sicherheitsäquivalent gleich groß wie er Erwartungswert μ
Risikofreude = Sicherheitsäquivalent ist größer als Erwartungswert
Risikoscheu = Sicherheitsäquivalent ist kleiner als Erwartungswert
Bei einer sogenannten konkaven Nutzenfunktion muss das Sicherheitsäquivalent „link“ vom
Erwartungswert liegen und es ergibt sich Risikoscheu.
Für eine lineare Nutzenfunktion stimmen Erwartungswert und Sicherheitsäquivalent stets überein =
Risikoneutralität.
Eine konvexe Nutzenfunktion ist das Sicherheitsäquivalent immer größer als der Erwartungswert =
Risikofreude.
Bei der Bernoulli-Nutzenfunktion nach Friedman und Savage sind Risikoscheu und Risikofreude
in einer Graphik kombiniert. Dabei kommt das Axiomsystem ins Spiel:
 Ordnungsaxiom (siehe Seite 35)
 Stetigkeitsaxiom
 Substitutionsaxiom
 Dominanzaxiom
Entscheidung in der Spielsituation
Hier gibt es eine Vielfalt von möglichen „Spielen“. Es kann unterschieden werden zwischen
Konstantsummen-Spiel, oder Nullsummen-Spiel oder Spiel mit variabler Summe, aber man kann
auch noch unterscheiden, ob das Spiel nur strategische oder auch zufällige Elemente umfasst, ob
die Spieler sich absprechen dürfen oder nicht und ob sie über die Züge anderer Spieler voll
informiert sind oder nicht. Für das Zwei-Personen-Nullsummen-Spiel ist die Minimax bzw.
Maximax-Regel die rationale Entscheidungsregel. Da bei den meisten strategischen Spielen jeder
Spieler mehrfach „am Zug“ ist, wird in der Spieltheorie allgemein von Strategie statt von Aktion
gesprochen. Im Gegensatz zu den bisher bekannten Strategien (reine Strategien) werden die
Strategien, die aus Wahrscheinlichkeitsverteilungen bestehen, gemischte Strategien genannt.
Abschließend kann gesagt werden, dass die schwierigste Aufgabe, bei den ganzen Prozessen, in
der Aufstellung eines Entscheidungsmodells besteht.