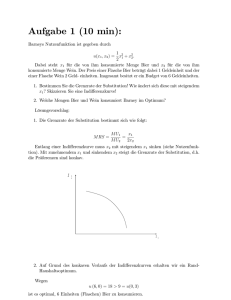
12. Uebung (23.01.2008

175.072 –Grundlagen der Wirtschaftswissenschaften UE –12. Übung
1. (2 Punkte) Zeichnen Sie die Einkommens-Konsum-Kurve und die Engelkurve für Gut 1 für
die folgenden Fälle in geeignete Diagramme ein:
(a) Leontief Präferenzen
(b) Lineare Nutzenfunktion
u(x1 ; x2 ) =
1 x1
+
2 x2 ;
1
> 0;
2
>0
(c) Verallgemeinerte Cobb Douglas Präferenzen
u (x1 ; x2 ) = Ax1 x2 ;
A > 0;
> 0;
>0
Anmerkung: Sie können bei der Beantwortung dieser Frage die bereits bekannten Ergebnisse
ohne neuerlichen Beweis verwenden.
2. (2 Punkte) Variieren Sie den Preis p1 ceteris paribus (d.h. bei unveränderten Werten von p2
und y). Zeichnen Sie die die Preis-Konsum-Kurve und die Nachfragekurve für Gut 1 für die
folgenden Fälle in geeignete Diagramme ein:
(a) Leontief Präferenzen
(b) Lineare Nutzenfunktion
(c) Verallgemeinerte Cobb Douglas Präferenzen
Anmerkung: Sie können bei der Beantwortung dieser Frage die bereits bekannten Ergebnisse
ohne neuerlichen Beweis verwenden.
3. (2 Punkte) Unterstellen Sie, dass der Preis p1 ceteris paribus (d.h. bei unveränderten Werten von p2 und y) steigt. Unterstellen Sie weiters, dass die beiden Güter für alle (p; y)Kombinationen normal sind. Zerlegen Sie den Gesamte¤ekt dieser Preisänderung graphisch
auf 2 Arten in den Substitutionse¤ekt und den Einkommense¤ekt, und zwar gemäß
(a) Hicks und
(b) Slutsky.
4. (2 Punkte) Unterstellen Sie, dass der Preis p1 ceteris paribus (d.h. bei unveränderten Werten
von p2 und y) steigt. Zerlegen Sie den Gesamte¤ekt dieser Preisänderung graphisch in den
Substitutionse¤ekt gemäßHicks und den Einkommense¤ekt, und zwar für
(a) Leontief Präferenzen
(b) Verallgemeinerte Cobb Douglas Präferenzen
Anmerkung: Sie können bei der Beantwortung dieser Frage die bereits bekannten Ergebnisse
ohne neuerlichen Beweis verwenden.
5. (2 Punkte) Unterstellen Sie, dass die Präferenzen durch die folgende Nutzenfunktion beschrieben werden:
1=2
1=2
u (x1 ; x2 ) = (x1 ) + (x2 )
(a) Kann bei diesen Präferenzen der Gi¤en-Fall auftreten?
(b) Gibt es (p; y)-Kombinationen, bei denen eines der beiden Güter inferior ist?
(c) Sind die beiden Güter Bruttosubstitute oder -komplemente?
Zusatzfragen für Studierende, die sich unterfordert fühlen
(nur für Freiwillige)
1. Bestimmen Sie die Einkommens-Konsum-Kurve und die Engelkurve für Gut 1 für den folgenden Spezialfall von quasilinearen Präferenzen:
u(x1 ; x2 ) =
(x1 ) + x2
wobei die Funktion : R+ ! R zweimal stetig di¤erenzierbar ist und
0
(x1 ) > 0;
lim
x1 !0
0
(x1 ) = 1;
lim
x1 !1
0
(x1 ) = 0;
00
(x1 ) < 0
gilt.
2. Homothetische Präferenzen: Unterstellen Sie, dass die Nutzenfunktion die folgende Form
hat:
u (x1 ; x2 ) = F (f (x1 ; x2 ))
wobei die Funktion f : X ! R, mit X = R2+ , homogen vom Grad k > 0 ist, d.h.
f ( x1 ; x2 ) =
k
f (x1 ; x2 )
für alle
> 0;
und die Funktion F : R ! R eine streng monoton wachsende Funktion ist. Bestimmen Sie die
Einkommens-Konsum-Kurve und die Engelkurven.
3. Unterstellen Sie, dass der Preis p1 ceteris paribus (d.h. bei unveränderten Werten von p2 und
y) steigt. Zerlegen Sie den Gesamte¤ekt dieser Preisänderung graphisch in den Substitutionse¤ekt gemäßHicks und den Einkommense¤ekt, und zwar für für folgenden Spezialfall von
quasilinearen Präferenzen:
u(x1 ; x2 ) =
(x1 ) + x2
wobei die Funktion : R+ ! R zweimal stetig di¤erenzierbar ist und
0
(x1 ) > 0;
lim
x1 !0
0
(x1 ) = 1;
gilt.
2
lim
x1 !1
0
(x1 ) = 0;
00
(x1 ) < 0