DARSTELLUNGSFORMEN VON KOMPLEXEN ZAHLEN

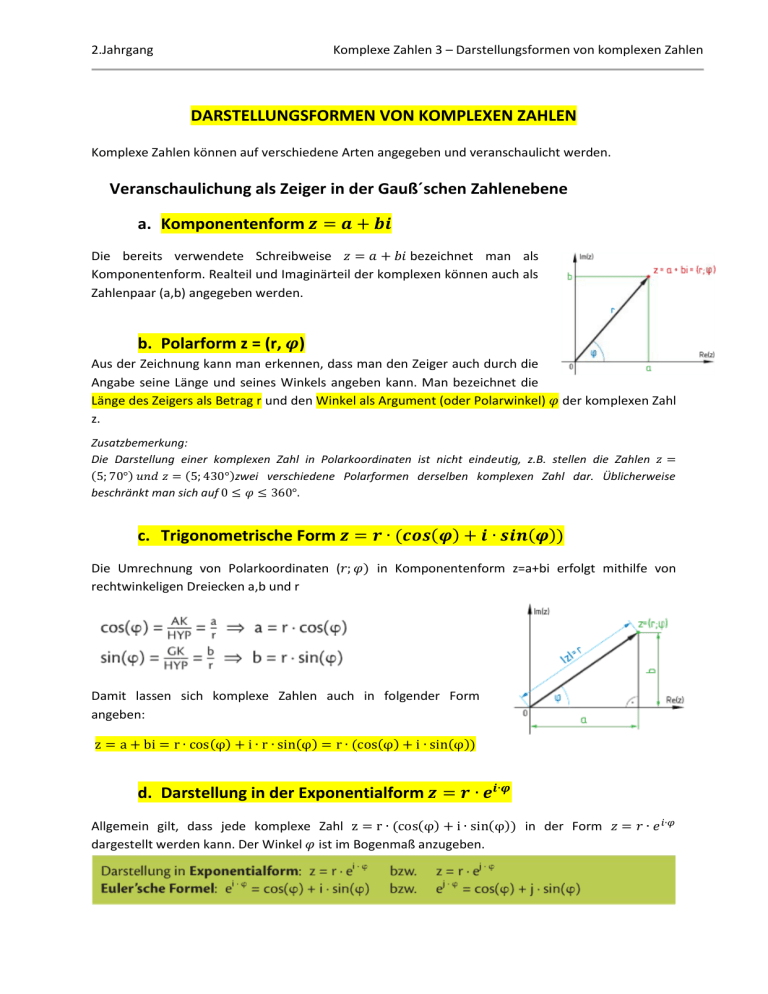
2.Jahrgang
Komplexe Zahlen 3 – Darstellungsformen von komplexen Zahlen
DARSTELLUNGSFORMEN VON KOMPLEXEN ZAHLEN
Komplexe Zahlen können auf verschiedene Arten angegeben und veranschaulicht werden.
Veranschaulichung als Zeiger in der Gauß´schen Zahlenebene
a. Komponentenform
Die bereits verwendete Schreibweise
bezeichnet man als
Komponentenform. Realteil und Imaginärteil der komplexen können auch als
Zahlenpaar (a,b) angegeben werden.
b. Polarform z = (r, )
Aus der Zeichnung kann man erkennen, dass man den Zeiger auch durch die
Angabe seine Länge und seines Winkels angeben kann. Man bezeichnet die
Länge des Zeigers als Betrag r und den Winkel als Argument (oder Polarwinkel)
z.
der komplexen Zahl
Zusatzbemerkung:
Die Darstellung einer komplexen Zahl in Polarkoordinaten ist nicht eindeutig, z.B. stellen die Zahlen
(
)
(
)zwei verschiedene Polarformen derselben komplexen Zahl dar. Üblicherweise
beschränkt man sich auf
(
c. Trigonometrische Form
( )
( ))
) in Komponentenform z=a+bi erfolgt mithilfe von
Die Umrechnung von Polarkoordinaten (
rechtwinkeligen Dreiecken a,b und r
Damit lassen sich komplexe Zahlen auch in folgender Form
angeben:
( )
( )
(
( )
( ))
d. Darstellung in der Exponentialform
( )) in der Form
Allgemein gilt, dass jede komplexe Zahl
( ( )
dargestellt werden kann. Der Winkel ist im Bogenmaß anzugeben.