Mathe 1: Zahlbereich 1 bis 10
Werbung
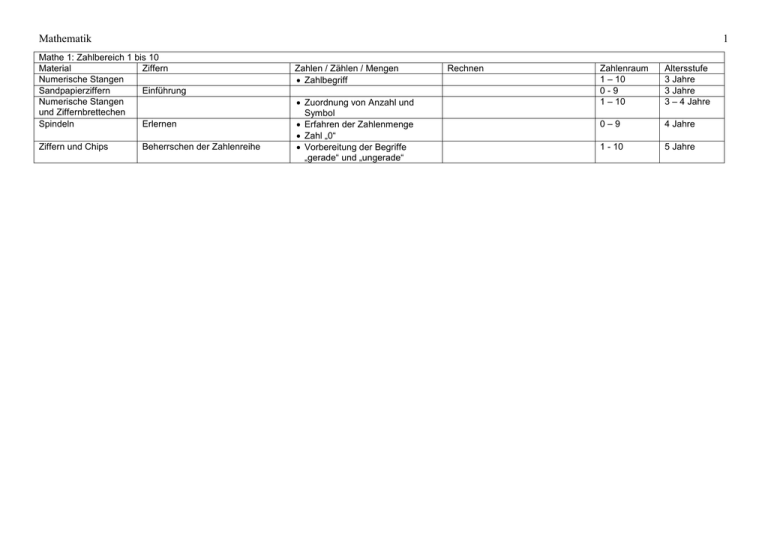
Mathematik 1 Mathe 1: Zahlbereich 1 bis 10 Material Ziffern Numerische Stangen Sandpapierziffern Einführung Numerische Stangen und Ziffernbrettechen Spindeln Erlernen Ziffern und Chips Beherrschen der Zahlenreihe Zahlen / Zählen / Mengen Zahlbegriff Zuordnung von Anzahl und Symbol Erfahren der Zahlenmenge Zahl „0“ Vorbereitung der Begriffe „gerade“ und „ungerade“ Rechnen Zahlenraum 1 – 10 0-9 1 – 10 Altersstufe 3 Jahre 3 Jahre 3 – 4 Jahre 0–9 4 Jahre 1 - 10 5 Jahre Mathematik 2 Mathe 2: Einführung in das Dezimalsystem Material Ziffern Goldenes Perlenmaterial Großer Kartensatz Goldenes Perlenmaterial und Kartensätze (Wechselspiel) Zahlen / Zählen / Mengen Mächtigkeit und Darstellungsform von Einern, Zehnern, Hundertern und Tausendern Namen der Stellenwerte des Dezimalsystems kennen lernen Struktur des Dezimalsystems erfahren Zahlensymbole für Zehner, Hunderter und Tausender Zuordnen von Mengen und Zahlsymbolen Einsicht in die Struktur des Dezimalsystems erlangen Fertigkeit im Umwechseln gewinnen Rechnen Zahlenraum 1 – 9.999 Altersstufe 4 Jahre 1 – 1.999 5 Jahre 1 – 9.999 5 Jahre Mathematik 3 Mathe 3: Lineares Zählen Material Ziffern Farbige Perlentreppchen Farbige Perlentreppe Kennenlernen der Zahlsymbole und Seguin-Tafel I von 11 – 19 Seguin-Tafel II Kurze Perlenkette Hunderterkette Tausenderkette Kennen lernen der Symbole für die Mengen 11 - 99 Zahlen / Zählen / Mengen Einüben des Zählens Einprägen der Zahlenfolge Benennen der Zahlenmengen von 1 – 19 Einprägen der Zahlenfolge 11 -1 9 Kennen lernen der Zahlensymbole von 11 – 19 Zuordnen von Zahlsymbolen zu den Zahlenmengen 11 – 19 Bilden der Mengen von 11 – 99 Zuordnung von Menge und Symbol Einprägen der Zahlenfolge von 11 - 99 Festigung des linearen Zählens rhythmisches Zählen (Überspringen von Zahlen) Erfassen der unterschiedlichen Darstellung von Mengen (Linie, Quadrat) Einüben der Zahlen bis 100 Festigung des Zählens Einüben der Zahlenreihe bis 1000 Festigung des Zählens Rechnen Indirekte Vorbereitung der Multiplikation Zahlenraum 1–9 5 Jahre 1 -19 5 Jahre 11 - 99 5 Jahre 1 - 100 5 Jahre 1 - 100 5 Jahre 1 – 1.000 6 Jahre Mathematik Mathe 4: Operationen im Dezimalsystem Material Ziffern Goldenes Perlenmaterial 4 Zahlen /Zählen / Mengen Markenspiel Punktspiel Kleiner Rechenrahmen Hierarchie der Zahlen Einsicht in das Prinzip des Stellenwertsystems Zuordnen von Einheiten zu Stellenwerten Das Prinzip der Bündelung von je 10 Einheiten zu einem höheren Stellenwert erkennen und üben Übergehen zu einer abstrakten Zahlendarstellung Dezimales Zählen Üben der Stellenwertübergänge Zählen und Notieren der Stellenwerte Erweiterung des Zahlenraums bis 1.000.000 Die Mächtigkeit der einzelnen Stellenwerte sollen dem Kind „begreifbar“ werden Verdeutlichung der Verhältnisse der einzelnen Stellenwerte untereinander Einführung in die Namen und Symbole für den erweiterten Zahlenraum bis 1.000.000 Rechnen Einsicht in das Wesen der Grundrechenarten: Addition, Multiplikation, Subtraktion, Division Erkennen der Bedeutung der Struktur des Dezimalsystems bei der Durchführung der Grundrechenarten Vertiefung der Einsicht in die Struktur des Dezimalsystems und in das Wesen der vier Grundrechenarten Vorbereiten der schriftlichen Addition Zahlenraum 1 – 9.999 5 Jahre 1 – 9.999 5 – 6 Jahre 1 – 99.999 6 – 7 Jahre Addieren und Subtrahieren von bis zu vierstelligen Zahlen Vorbereitung des schriftlichen Additions- und Subtraktionsverfahrens 1 – 10.000 6 Jahre 1– 1.000.000 6 Jahre Mathematik 5 Großer Rechenrahmen Großes Multiplikationsbrett (Schachbrett) Liegender Rechenrahmen Bankspiel Große Division (Apotheke) Vertiefung der Einsicht in das Dezimalsystem Addieren, Subtrahieren und Multiplizieren von bis zu siebenstelligen zahlen mit dezimalwertigen Perlen Vorbereitung der Addition und Subtraktion Multiplizieren mehrstelliger Zahlen mit ein- oder mehrstelligem Multiplikator Üben des Einmaleins Vertiefen des Wesens der Multiplikation Erlernen der schriftlichen Multiplikation Multiplizieren mit ein- bis vierstelligem Multiplikator Hinführen zur schriftlichen Multiplikation Umgang mit großen, bis zu siebenstelligen Zahlen Einmaleins der großen Zahlen Analyse der Multiplikation eines vierstelligen Multiplikanden mit dreistelligem Multiplikator ohne Zuhilfenahme abzählbaren Materials Verteilen großer, bis siebenstelliger Dividenden an ein- bis mehrstellige Divisoren Hinführen zum schriftlichen Divisionsverfahren 1– 10.000.000 7 Jahre 1999.999.999 6 Jahre 1999.999.999 8 Jahre 1– 9.999.999 8 Jahre 1– 9.999.999 6 Jahre Mathematik Mathe 5: Grundaufgaben der Addition, Subtraktion, Multiplikation und Division Material Ziffern Zahlen / Zählen / Mengen Schlangenspiel zur Addition Streifenbrett zur Addition Additionstabelle Schlangenspiel zur Subtraktion und Negatives Schlangenspiel Streifenbrett zur Subtraktion Subtraktionstabellen 6 Rechnen Addieren durch Zählen Addieren von Einern Ergänzen zu 10 Zerlegen der Zahlen 2 - 9 Erkennen, Üben und Einprägen aller Grundaufgaben der Addition mit einstelligen Summanden (81 Stück) Einsicht in das Wesen der Addition: Vertauschbarkeit der Summanden, Zerlegen der Summanden, Ergänzen zu 10, Zehnerüberschreitung Einüben und Einprägen aller Grundaufgaben der Addition mit den Summanden 1 bis 9 Anwenden des Vertauschungsgesetzes Ermitteln von Summanden zu vorgegebenen Summen Einführung in die Grundaufgaben der Subtraktion von 18 – 9 bis 1 – 1 Addieren und Subtrahieren im Bereich der ganzen Zahlen Zahlenraum 1-9 5 Jahre 1 - 18 5 Jahre 1 - 18 6 Jahre -18 - +18 Erkennen und Üben aller Grundaufgaben der Subtraktion im Zahlbereich 1 bis 18 Einsicht in das Wesen der Subtraktion: Zerlegen des Subtrahenden, Unterschreiten des Summanden Einüben aller Grundaufgaben der Subtraktion im Zahlenraum 1 bis 18 1 – 18 6 Jahre (positive Zahlen) 8 Jahre (ganze Zahlen) 6 Jahre 1 - 18 6 Jahre Mathematik Perlenstäbchen zur Multiplikation Kleines Multiplikationsbrett Multiplikationstabellen Divisionsbrett Divisionstabellen 7 Gewinnen von Einsicht in die Struktur der Einmaleinsreihen Memorieren der Einmaleinsreihen Geometrische Darstellung von Multiplikationen Erkennen des Multiplikators als Operator, der bestimmt, wie oft der Multiplikand malgenommen wird Vergleich geometrischer und dekadischer Darstellung Geometrische Darstellung von Einmaleinsreihen Ermitteln der Produkte durch Zählen Erstes Einprägen von Einmaleinsaufgaben Einüben aller Grundaufgaben des kleinen Einmaleins Anwendung des Vertauschungsgesetzes Grunderfahrungen mit dem kleinen Einsdurcheins Herstellen der Beziehung zur Multiplikation Einüben aller Grundaufgaben der Division 1 – 100 5 Jahre 1 - 100 5 Jahre 1 -100 6 Jahre 1 -81 5 Jahre 1 - 81 6 Jahre Mathematik Mathe 6: Potenzen Material Perlenregal 8 Ziffern Zahlen / Zählen / Mengen Vergleich der verschiedenen Potenzdarstellung Ordnen von verschiedenen Potenzdarstellungen Lineares Zählen in Einerschritten und Basisschritten Mächtigkeitsvergleich der verschiedenen Potenzdarstellungen Lineare, flächige und räumliche Erfassung von Zahlen Kardinalzahl und Ordinalzahl Rechnen Hinführung zur Potenzrechnung Zahlenraum 1 - 1000 6 Jahre Mathematik Mathe 7: Rechnen mit gebrochenen Zahlen Material Ziffern Material zum Rechnen mit echten Brüchen Material zum Rechnen mit unechten Brüchen und gemischten Zahlen 9 Zahlen / Zählen / Mengen Darstellung von Brüchen Kennen lernen von Namen und Schreibweisen Gleichwertigkeit von Brüchen Darstellung von Brüchen Kennen lernen von Namen und Schreibweisen Unterschiede von Brüchen Umwandeln von unechten Brüchen und gemischten Zahlen Rechnen Addieren und Subtrahieren von gleichnamigen Brüchen Kürzen und Erweitern von Brüchen Multiplizieren von Brüchen mit ganzen Zahlen Dividieren von Brüchen durch ganze Zahlen Addieren und Subtrahieren von ungleichnamigen Brüchen Dividieren durch Brüche Entwickeln von Bruchrechenregeln Addieren und Subtrahieren von ungleichnamigen Brüchen Multiplizieren mit Brüchen Dividieren durch Brüche Ableiten von Regeln Zahlenraum