Klasse 9

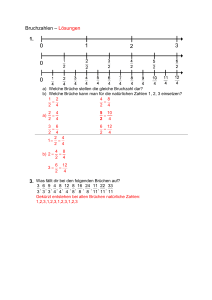
Klasse 6
Kapitel 1: Teilbarkeitslehre
1. Konzeptionelle Hinweise
Die Teilbarkeitslehre erfüllt im Rahmen der Bruchrechnung eine wichtige Hilfsfunktion. Andererseits möchte
man natürlich trotzdem eine Vermittlung durch eigenständige, motivierende Beispiele erreichen. In diesem
Sinne sind Übung 1 in Abschnitt 1.1.1 (Begriff der Teilbarkeit), Übung 1 in Abschnitt 1.3.1 (gemeinsame
Teiler und ggT) und Übung 4 in Abschnitt 1.3.3 (gemeinsame Vielfache) konzipiert worden. Höhere
Ansprüche werden durch Übung 7 in Abschnitt 1.3.5 gestellt.

Abschnitt 1.3 Übung 1
Abschnitt 1.3 Übung 4
Abschnitt 1.3 Übung 7
Abschnitt 1.3 Übung 7

2. Zur Begründungsproblematik der Teilbarkeitsregeln
Durch den Umgang mir Zahlen werden den Schülern wahrscheinlich gewisse Teilbarkeitsregeln vertraut sein.
Dies betrifft insbesondere die Teilbarkeit durch 2, 4, 5 und 10. Trotzdem liefert die entsprechende Lernseite
eine kurze Begründung. Alle formulierten Teilbarkeitsregeln gelten in der Form ... genau dann... .
Interessant und in der Begründung nicht ganz so einfach sind die Regeln für die Teilbarkeit durch 3 und 9. Für
die Teilbarkeit durch 3 wird diese in Übung 4 von Abschnitt 1.1.3 erarbeitet. Die Übung stellt insofern einen
Beitrag zur Beweispropädeutik bzw. Kompetenz Argumentieren (vgl. Kernlehrplan NRW) dar, als man
erkennt, dass die für konkrete Zahlen erarbeitete Begründung auf beliebige Zahlen übertragbar ist. Sie liefert im
Übrigen die Begründung für beide logischen Richtungen. Man erkennt, dass eine Zahl dann und nur dann durch
3 teilbar ist, wenn dies für die Quersumme gilt.
1

Abschnitt 1.1 Übung 4
Wie weit bei Schülern eine erste Sensibilisierung für logische Richtungen erreichbar ist, ist natürlich eine
schwierige Frage, zumal im Zusammenhang mit der Teilbarkeitslehre nur Sätze auftreten, für die beide
Richtungen stimmen.
Kapitel 2: Bruchrechnung
1. Gesamtkonzeption
Ein wesentliches Ziel liegt darin, von Brüchen und Bruchzahlen sowie den Verknüpfungen zwischen ihnen eine
klare inhaltliche Vorstellung zu erarbeiten. Dies betrifft das Erweitern und Kürzen, die Addition und
Subtraktion und insbesondere die Multiplikation und Division.
Bruchzahlen sind Äquivalenzklassen von Brüchen. Formal muss daher zwischen Brüchen und Bruchzahlen
unterschieden werden und bei den Verknüpfungen die Repräsentantenunabhängigkeit gesichert sein.
Natürlich sind hierzu formale Überlegungen in der Klasse 6 unangebracht. Das Problem der
Repräsentantenunabhängigkeit erledigt sich mit Blick auf die Schüler dadurch, dass die Rechenoperationen an
Bruchteilen konkreter Größen eingeführt werden und damit an inhaltliche und geometrische Vorstellungen
angebunden werden.
Auch die sprachliche Unterscheidung zwischen Brüchen und Bruchzahlen würde an vielen Stellen schwerfällig
wirken ohne dass dadurch zusätzliche Klarheit gewonnen würde. Daher und wegen der inhaltlichen
Einkleidungen ist es vielfach durchaus akzeptabel, von der Multiplikation oder Addition von Brüchen zu
sprechen, wenn zugleich die entsprechenden Operationen für Bruchzahlen gemeint sind.
Ein besonders wichtiger Punkt ist die Einführung der Multiplikation von Brüchen. Hier müssen klare
Vorstellungen zur inhaltlichen Interpretation herausgearbeitet werden. Genaueres findet sich unter 4.
2. Bruchzahlen und ihre Veranschaulichung; Erweitern und Kürzen
Bereits mit den ersten geometrischen Veranschaulichungen von Brüchen tritt das Kürzen ins Blickfeld. Es lässt
sich daher im Zusammenhang mit Übung 1 in Abschnitt 2.1.1 kaum vermeiden, dass Schüler auch ungekürzte
Darstellungen verwenden. Das Programm akzeptiert diese (natürlich!) als richtig, macht aber zugleich auf die
Möglichkeit des Kürzens aufmerksam. Es wird daher auf der entsprechenden Lernseite informell kurz
eingeführt. Die systematische Behandlung erfolgt allerdings erst in Abschnitt 2.1.3.
Das Erweitern stellt einen wichtigen Prozess für die Einführung der Addition dar. Andererseits erscheint es
sinnvoll, eine eigenständige inhaltliche Motivation anzustreben, was in Übung 3, Abschnitt 2.1.2 geschieht.
2

Abschnitt 2.1 Übung 1
Abschnitt 2.1 Übung 3
Wichtig ist auch das geometrische Verständnis des Erweiterns und Kürzens als Verfeinerung bzw.
Vergröberung von Einteilungen. Das Programm setzt hier immer wieder durch entsprechende geometrische
Darstellungen (auch als abrufbare Hilfen) Akzente.
3. Addition und Subtraktion
Die Addition gleichnamiger Brüche ist problemlos. Im Zusammenhang mit der Addition beliebiger Brüche
wird das Erweitern bedeutsam: Durch eine gemeinsame Verfeinerung zweier Einteilungen wird die Addition
möglich. Die Hilfestellungen in Abschnitt 2.2.1, Übung 1 machen diesen wichtigen Aspekt in jeder Aufgabe
veranschaulichend deutlich. Der Aufruf der Hilfe ist somit auch nach der Bearbeitung einer Aufgabe zu
empfehlen.

Abschnitt 2.2 Übung 1
4. Multiplikation und Division von Brüchen
Während die Multiplikation eines Bruches mit einer natürlichen Zahl naheliegend als mehrfache Addition
verstanden werden kann, stellt die Multiplikation von Brüchen (Bruchzahlen) eine wichtige Gelenkstelle dar.
Eine Schlüsselfunktion nimmt Übung 3 in Abschnitt 2.3.2 ein: Es geht darum, von der Multiplikation eine
operative inhaltliche Vorstellung zu gewinnen und sie als (einzig) sinnvolle Fortsetzung der Multiplikation
mit natürlichen Zahlen zu verstehen. Die Einzelheiten gehen aus der Übung selbst sowie dem zugehörigen
Lerntext hervor. Geeignete Textaufgaben (vgl. Abschnitt 2.3.6, Übung 6) dienen der weiteren Sicherung der
inhaltlichen Vorstellungen. Die Division wird naheliegend über die Multiplikation eingeführt.
Gemäß dem didaktischen Prinzip des vorwegnehmenden Lernens werden die Schüler bereits vor der
Einführung (Definition) der Multiplikation von Brüchen auf den Umgang mit Bruchteilen von Brüchen
vorbereitet. Dies geschieht in den Übungen zu den Abschnitten 2.1.6 bis 2.1.8.
3

Abschnitt 2.3 Übung 3
Abschnitt 2.3 Übung 6
Dass die Berechnungsvorschriften für die Inhalte einfacher Flächen bzw. für Volumina einfacher Körper im
Bereich der Brüche als Seitenmaßzahlen gültig bleiben, bedarf jeweils einer besonderen Begründung. Sie
findet sich in Abschnitt 2.3.4, Übung 6 bzw. in Abschnitt 2.3.5, Übung 8.
4. Tests und Fehlerdiagnosen
Abschnitt 2.4 bietet bewertete Tests zu den Verfahren an, die in Kapitel 2 erarbeitet wurden. In Abschnitt 2.5
befinden sich Diagnoseübungen. Es geht darin nicht nur um die Sicherung des rechnerischen Umgangs mit
Bruchzahlen. Insbesondere Multiplikation und Division müssen mit Blick auf Anwendungen mit klaren
inhaltlichen Vorstellungen verbunden werden. Diese werden einerseits in Form von Veranschaulichungen und
andererseits durch Kommentare gestützt. Zumindest teilweise sind daher die Aufgaben so gestellt, dass man
ohne viel Rechenaufwand das richtige Ergebnis mithilfe einer adäquaten Vorstellung erkennt. Übung 2
ermöglicht durch Setzen bzw. Beseitigen von Klammern das Erreichen eines vorgegebenen Resultats. Auch
hier ist es wichtig, nicht zu probieren, sondern aufgrund der Veranschaulichung des Resultats gestützt auf eine
inhaltliche Vorstellung der Rechenoperationen gezielt die Klammern zu setzen. Ein erläuterndes Beispiel dazu
findet sich auf der zur Übung gehörigen Lernseite.
Abschnitt 2.5 Übung 1
Abschnitt 2.5 Übung 2
Die beiden Übungen bieten sich im unteren Teil dazu an, sich eigenständig weitere Aufgaben zu stellen und
diese kontrollieren zu lassen.
Kapitel 3: Dezimalbrüche
4
Das Kapitel ist in seiner Struktur und im Stellenwert der einzelnen Übungen weitgehend selbsterklärend. Einen
Hinweis verdient allerdings Abschnitt 3.4.3: Die Einführung periodischer Dezimalbrüche liefert die
Möglichkeit, die Schüler in vorsichtiger Weise an Grenzwertvorstellungen zu gewöhnen.
Kapitel 4: Geometrie
1. Ein wichtiger Hinweis
In dem Kapitel werden mehrfach Konstruktionen abverlangt. Es besteht die Möglichkeit, diese in dem
mitgelieferten Programm „Zeichenblatt“ durchzuführen. Es ist dem üblichen Zeichnen mit Zirkel und
Geodreieck nachempfunden und kann parallel zum Lernprogramm durch Umschalten benutzt werden.

Zusatzprogramm: Zeichenblatt
2. Grundbegriffe
Strecke, Gerade, Strahl, Parallelität und Orthogonalität sind Begriffe, die bereits aus der Klasse 6 vertraut sind.
Sie werden in Abschnitt 4.1.2, Übung 2 noch einmal kurz wiederholt. Der neue Begriff „Winkel“ wird
kontextbezogen an einem interessanten Phänomen (Drehung des Fixsternhimmels; Simulation) eingeführt
(Abschnitt 4.1.3, Übung 3) und im Abschnitt 4.1.5, Übung 5 konstruktiv genutzt. Übung 5 bietet zudem die
Möglichkeit, eine Konstruktionsbeschreibung abzurufen.

Abschnitt 4.1 Übung 2
Abschnitt 4.1 Übung 3
5

Abschnitt 4.1 Übung 5
3. Abbildungen
Thema sind die drei Abbildungstypen Achsenspiegelung, Drehung und Verschiebung. Besonders interessant ist
die in Übung 3 behandelte Extremwertaufgabe. Die Lösung erscheint auf dem ersten Blick sehr schwierig, ist
jedoch nach Durchführung einer geeigneten Spiegelung geradezu trivial. Die Abbildungen selbst stehen in
einem engen Zusammenhang zu Symmetrieen, die in Abschnitt 4.3 thematisiert werden.

Abschnitt 4.2 Übung 3
Abschnitt 4.3 Übung 3
6