Zahlenbereiche - knowledge-base
Werbung
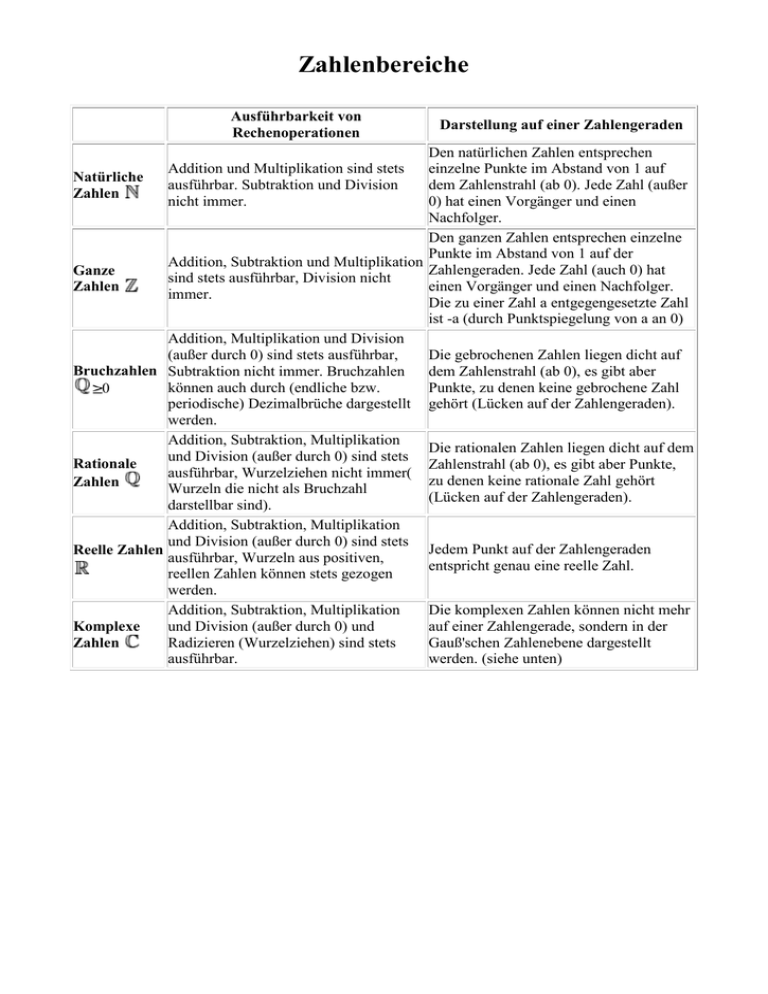
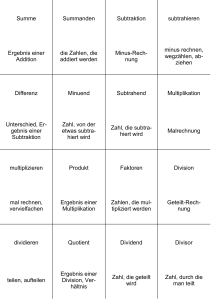
Zahlenbereiche Ausführbarkeit von Rechenoperationen Darstellung auf einer Zahlengeraden Den natürlichen Zahlen entsprechen einzelne Punkte im Abstand von 1 auf Natürliche dem Zahlenstrahl (ab 0). Jede Zahl (außer Zahlen 0) hat einen Vorgänger und einen Nachfolger. Den ganzen Zahlen entsprechen einzelne Punkte im Abstand von 1 auf der Addition, Subtraktion und Multiplikation Zahlengeraden. Jede Zahl (auch 0) hat Ganze sind stets ausführbar, Division nicht einen Vorgänger und einen Nachfolger. Zahlen immer. Die zu einer Zahl a entgegengesetzte Zahl ist -a (durch Punktspiegelung von a an 0) Addition, Multiplikation und Division (außer durch 0) sind stets ausführbar, Die gebrochenen Zahlen liegen dicht auf Bruchzahlen Subtraktion nicht immer. Bruchzahlen dem Zahlenstrahl (ab 0), es gibt aber können auch durch (endliche bzw. Punkte, zu denen keine gebrochene Zahl 0 periodische) Dezimalbrüche dargestellt gehört (Lücken auf der Zahlengeraden). werden. Addition, Subtraktion, Multiplikation Die rationalen Zahlen liegen dicht auf dem und Division (außer durch 0) sind stets Rationale Zahlenstrahl (ab 0), es gibt aber Punkte, ausführbar, Wurzelziehen nicht immer( zu denen keine rationale Zahl gehört Zahlen Wurzeln die nicht als Bruchzahl (Lücken auf der Zahlengeraden). darstellbar sind). Addition, Subtraktion, Multiplikation und Division (außer durch 0) sind stets Jedem Punkt auf der Zahlengeraden Reelle Zahlen ausführbar, Wurzeln aus positiven, entspricht genau eine reelle Zahl. reellen Zahlen können stets gezogen werden. Addition, Subtraktion, Multiplikation Die komplexen Zahlen können nicht mehr und Division (außer durch 0) und auf einer Zahlengerade, sondern in der Komplexe Radizieren (Wurzelziehen) sind stets Gauß'schen Zahlenebene dargestellt Zahlen ausführbar. werden. (siehe unten) Addition und Multiplikation sind stets ausführbar. Subtraktion und Division nicht immer. Komplexe Zahlen: Komplexe Zahlen in Normalform Rechenoperationen mit komplexen Zahlen in Normalform Komplexe Zahlen in trigonometrischer Form Rechenoperationen mit komplexen Zahlen in trigonometrischer Form Beispiel für die grafische Addition bzw. Subtraktion komplexer Zahlen Quelle: "Das große Tafelwerk" Cornelsen Verlag